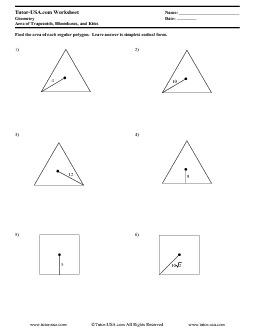
Worksheets Area of Kite

The area of a kite is a crucial concept in geometry. Understanding how to calculate the area of this unique shape can greatly enhance your knowledge and problem-solving skills. Whether you're a student looking to reinforce your grasp on the topic or a teacher searching for valuable resources to supplement your lessons, utilizing worksheets can provide the perfect opportunity to master the calculation of the area of a kite in a structured and effective manner.

  Rhombus and Kite Area Worksheet

---

  Kites Worksheets Printable

---

  Area Quadrilateral Worksheet

---

  Geometry Area of Regular Polygons Worksheet

---

  Area Parallelogram Worksheet

---

  Kite Worksheet

---

  Types of Quadrilaterals Worksheet

---

  Quadrilateral Angles Worksheet

---

  Area and Perimeter Worksheets 6th Grade

---

  Kites Worksheets Printable

---

What is a kite in geometry?

In geometry, a kite is a quadrilateral with two distinct pairs of adjacent sides that are congruent. This means that the sides next to each other are equal in length, but the pairs of sides are not necessarily equal to each other. Additionally, a kite has one pair of opposite angles that are congruent. The diagonals of a kite are also perpendicular to each other, with one diagonal bisecting the other.

How do you find the area of a kite?

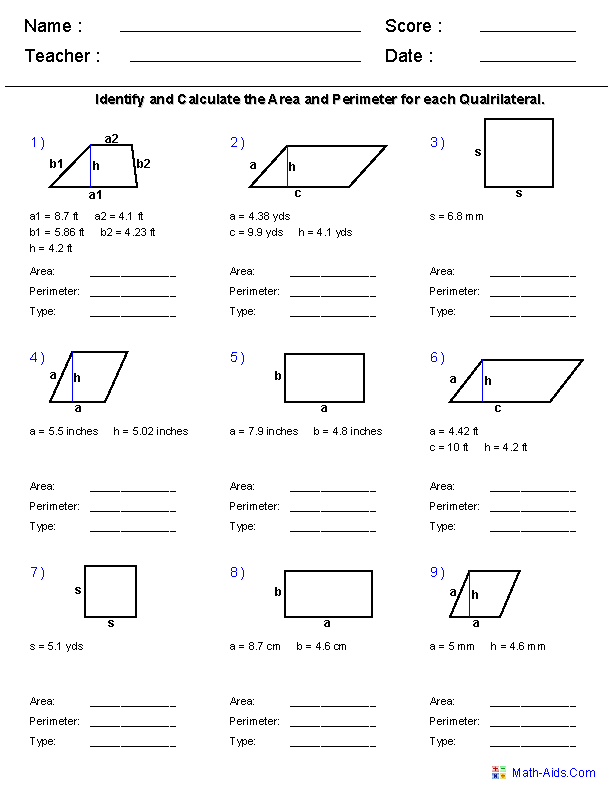
To find the area of a kite, you can use the formula: Area = (diagonal 1 x diagonal 2) / 2, where the diagonals are the two line segments that intersect each other at the kite's center point. Measure the lengths of the two diagonals, multiply them, and then divide the result by 2 to calculate the area of the kite.

What is the formula for finding the area of a kite?

The formula for finding the area of a kite is A = (d1 * d2) / 2, where d1 and d2 represent the lengths of the diagonals of the kite and "A" is the area.

Can all the sides of a kite have the same length?

No, a kite cannot have all sides of the same length. A kite by definition has two pairs of adjacent sides that are equal in length, but the pairs are not equal to each other. This means that the lengths of the sides are typically different, as the longer pair is not equal to the shorter pair in a typical kite shape.

How many diagonals does a kite have?

A kite has two diagonals.

What is the relationship between the diagonals of a kite?

In a kite, the diagonals are perpendicular to each other. This means that they intersect at a 90-degree angle, dividing the kite into four right-angled triangles. Additionally, the diagonals of a kite are not necessarily congruent, but they bisect each other at their point of intersection.

Can a kite have a right angle?

Yes, a kite can have a right angle if it is a special type of kite known as a right kite. A right kite is a quadrilateral with one pair of consecutive sides of equal length and one pair of consecutive angles that are equal and each measure 90 degrees, forming a right angle.

How do you calculate the length of the diagonals of a kite?

To calculate the length of the diagonals of a kite, you can use the formula sqrt(a^2 + b^2), where 'a' and 'b' are the lengths of the two diagonals that intersect at a right angle. Square the lengths of each diagonal, add them together, and then take the square root of the sum to find the length of the diagonals.

Is the area of a kite always half the product of the diagonals?

Yes, the area of a kite is always half the product of the lengths of its diagonals because the diagonals of a kite are perpendicular bisectors of each other, dividing the kite into four right triangles with equal areas. Thus, the area of a kite can be calculated as half the product of the lengths of its diagonals.

Can a kite have equal adjacent angles?

No, a kite cannot have equal adjacent angles. A kite is a quadrilateral with two pairs of adjacent sides that are equal in length, but the adjacent angles are not equal. The two pairs of adjacent angles in a kite are usually not congruent unless the kite is a rhombus.