Two-Step Equations Worksheets with Answer Key
Two-step equations worksheets are a helpful resource for students who are learning or reviewing the concept of solving equations. These worksheets provide practice problems for students to work through, allowing them to strengthen their skills and confidence in solving equations with two steps. With the accompanying answer key, they can easily check their work and ensure accuracy.
Table of Images 👆
- Two-Step Equations Worksheet
- Literal Equations Worksheet Answer Key
- Two-Step Equations Worksheet
- Solving Two-Step Equations Worksheet Answers
- Books Never Written Math Worksheet Answers
- Multi-Step Equations Worksheets
- One Step Equations Answer Key
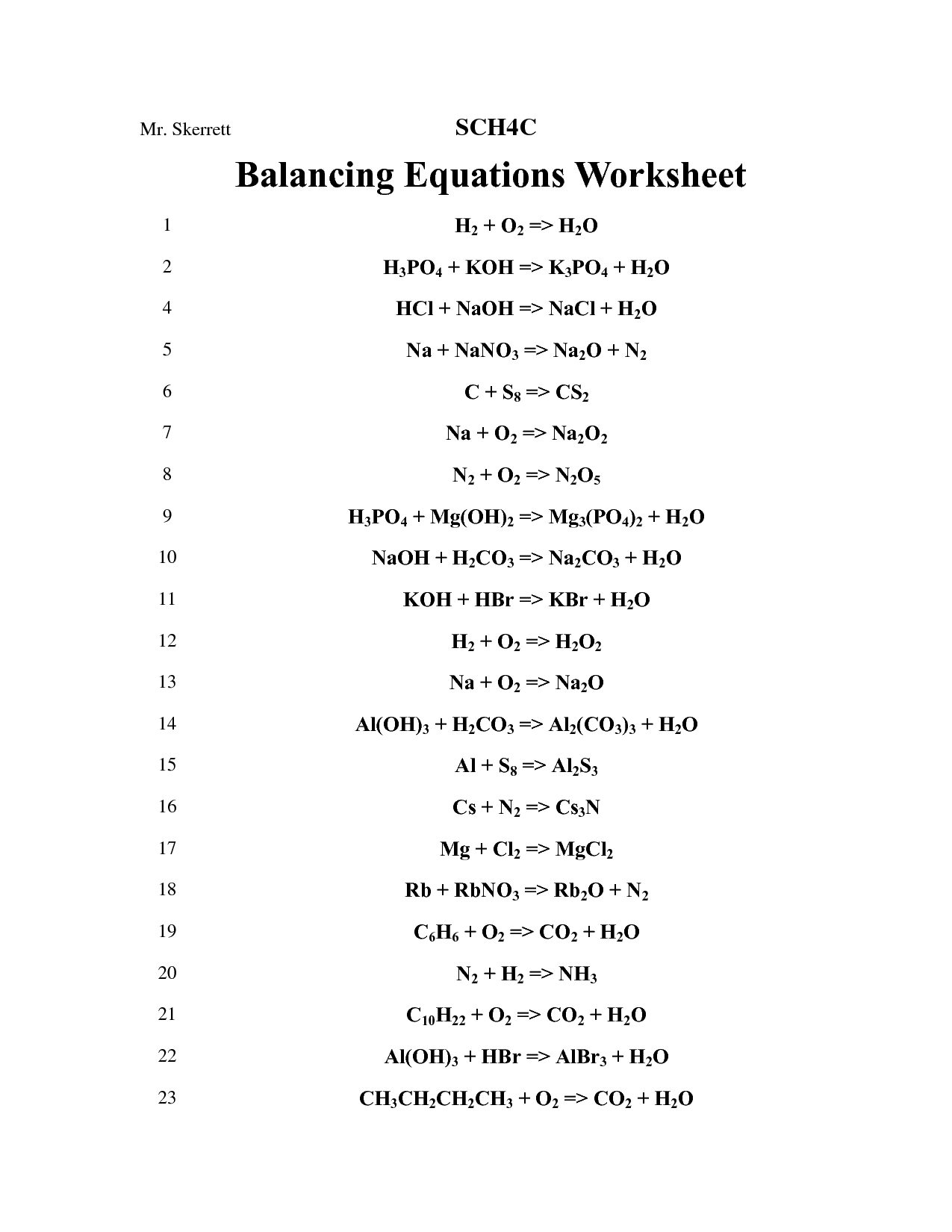
- Balancing Chemical Equations Worksheet Answer Key
- Solving Two-Step Equations Worksheet Answers
- Two-Step Equations Worksheet
- Solving Equations Worksheets
- Balancing Chemical Equations Worksheet
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What are two-step equations?
Two-step equations are algebraic equations that require two different operations to solve. This typically involves isolating the variable by performing two steps such as addition, subtraction, multiplication, or division on each side of the equation in order to find the value of the variable that makes the equation true.
How do you solve a two-step equation?
To solve a two-step equation, you first perform the inverse operation of addition or subtraction to isolate the variable term on one side of the equation. Next, perform the inverse operation of multiplication or division to solve for the variable. Follow the order of operations (PEMDAS) to simplify the equation step by step until you find the value of the variable that satisfies the equation.
What is the purpose of practicing two-step equations?
The purpose of practicing two-step equations is to develop problem-solving skills and improve algebraic understanding. It helps students to learn how to break down complex problems into smaller, manageable steps, and develop the ability to solve equations by performing multiple operations in a systematic manner. This skill is important for advancing in mathematics and other fields that require critical thinking and logical reasoning.
Can you provide an example of a two-step equation?
An example of a two-step equation is: 3x + 7 = 16. In this equation, you would first subtract 7 from both sides to isolate the variable, giving you 3x = 9. Then, you would divide both sides by 3 to solve for x, resulting in x = 3.
What are some common mistakes to avoid when solving two-step equations?
Some common mistakes to avoid when solving two-step equations include not following the correct order of operations, forgetting to perform the same operation on both sides of the equation, incorrectly distributing or combining like terms, and not simplifying fully to find the final solution. It is important to double-check each step and ensure that you are making accurate calculations to arrive at the correct answer for the two-step equation.
How can the answer key help when working on two-step equation worksheets?
The answer key can provide immediate feedback and allow for self-assessment when working on two-step equation worksheets. By checking the answers against the key, students can identify any mistakes, rectify errors, and understand the correct steps to solve the problems. Additionally, the answer key can serve as a guide for understanding the process and strategies involved in solving two-step equations, ultimately enhancing learning and problem-solving skills.
What are some strategies or tips for solving more challenging two-step equations?
One effective strategy for solving more challenging two-step equations is to first simplify the equation by combining like terms and grouping variables on one side. Then, isolate the variable by performing inverse operations in reverse order of operations, starting with addition or subtraction, followed by multiplication or division. Another tip is to clearly define each step and maintain accuracy by checking your work at each stage. Additionally, rewriting the equation in a different form, such as factoring or using the distributive property, can help simplify the problem and make it easier to solve.
How can two-step equations be applied to real-life situations?
Two-step equations can be applied to real-life situations in various ways, such as calculating expenses and budgeting, determining time and distance in travel scenarios, and solving for unknown quantities in measurements or construction projects. By using two-step equations, individuals can efficiently solve practical problems that involve multiple steps or operations, helping them make informed decisions and understand the relationships between different variables in everyday situations.
Are there any alternative methods for solving two-step equations?
Yes, there are alternative methods for solving two-step equations, such as using graphing or matrix methods. Graphing involves plotting the equations on a graph and finding the intersection point as the solution. Matrix methods involve setting up the equations in matrix form and using techniques such as row reduction to solve for the variables. These methods can be particularly useful in more complex systems of equations or when traditional algebraic methods are not feasible.
How can reviewing and practicing two-step equations improve overall algebraic skills?
Reviewing and practicing two-step equations can improve overall algebraic skills by enhancing problem-solving abilities, deepening understanding of algebraic principles, and honing critical thinking skills. By working through various two-step equations, individuals develop proficiency in manipulating symbols and equations, which forms the foundation for more complex algebraic problems. This practice also helps in mastering the concept of variables, coefficients, and constants, thereby improving algebraic reasoning and problem-solving techniques essential for advancing to higher levels of mathematics.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.

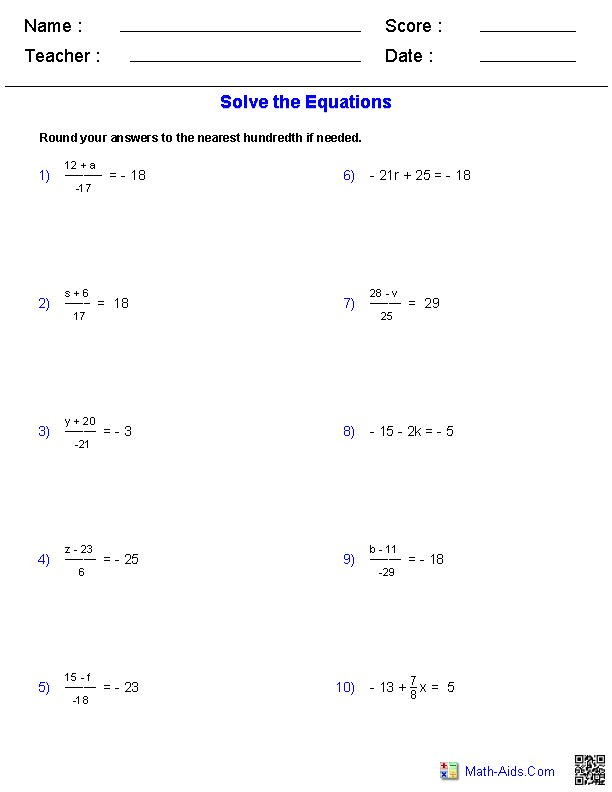

























Comments