Trig Functions Worksheet PDF
Trigonometric functions play a significant role in mathematics and are widely used in various academic fields such as physics, engineering, and computer science. If you're an educator or a student in need of additional practice and resources to deepen your understanding of trigonometric functions, you'll find this Trig Functions Worksheet PDF incredibly valuable. Designed to provide targeted exercises and reinforce key concepts, this worksheet will help you master the intricacies of trigonometry and excel in your studies.
Table of Images 👆
Trig Identities Formula Sheet
Right Triangle Trigonometry Word Problems
Accelerated Math Test Equations Circle
Trig Identities Worksheet
Unit Circle
Unit Circle Degrees
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What is a trigonometric function?
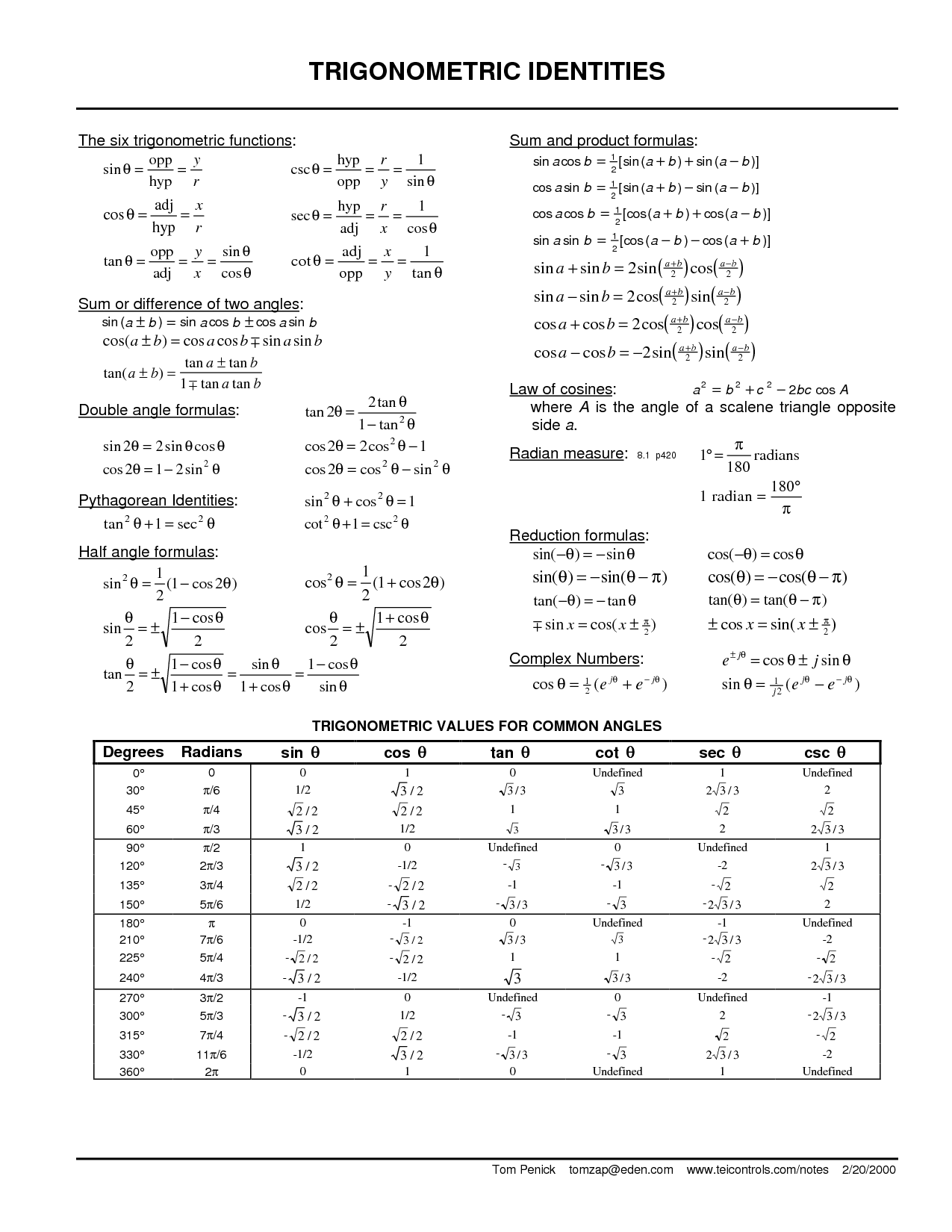
A trigonometric function is a mathematical function that relates angles of a right triangle to the lengths of its sides. The most common trigonometric functions are sine, cosine, and tangent, which represent the ratio of the lengths of certain sides of the triangle. These functions are fundamental in trigonometry and are used to model periodic phenomena and solve various mathematical problems involving angles and triangles.
What is the definition of the sine function?
The sine function is a trigonometric function that represents the ratio of the length of the side opposite an acute angle in a right triangle to the length of the hypotenuse. It is denoted as sin and is commonly used in mathematics to relate angles to the lengths of sides in right triangles or to oscillatory phenomena.
How is the cosine function related to the sine function?
The cosine function is related to the sine function through their relationship in the unit circle. Specifically, the cosine of an angle in a right triangle is defined as the ratio of the length of the adjacent side to the hypotenuse, while the sine is defined as the ratio of the length of the opposite side to the hypotenuse. This relationship is further represented in the trigonometric identity cos(x) = sin(x + ?/2), indicating that the cosine function is a phase-shifted version of the sine function.
What is the tangent function?
The tangent function is a trigonometric function that represents the ratio of the opposite side to the adjacent side in a right triangle. In other words, it is the ratio of the length of the side opposite to an acute angle to the length of the side adjacent to that angle. The tangent function is defined as the sine of an angle divided by the cosine of that angle and is commonly denoted as tan(theta) or tg(theta).
What is the reciprocal of the sine function?
The reciprocal of the sine function is the cosecant function, which is equal to 1 divided by the sine of an angle.
How can the values of the trigonometric functions be determined for specific angles?
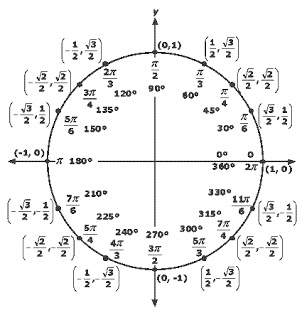
The values of trigonometric functions for specific angles can be determined by using the definitions of the functions and the unit circle. By understanding how sine, cosine, and tangent are related to the x and y coordinates on the unit circle, we can calculate the values for different angles. Additionally, trigonometric identities and properties can be applied to simplify and determine the values of trigonometric functions for specific angles.
What is the period of the tangent function?
The period of the tangent function is ?, which means it repeats its values every ? units or every 180 degrees.
How are the trigonometric functions used in geometry?
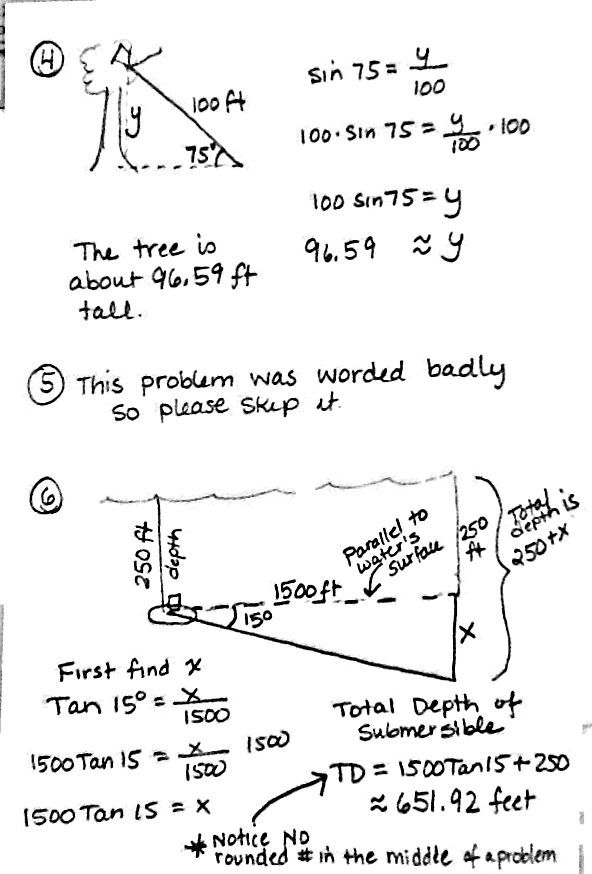
Trigonometric functions are used in geometry to calculate various measurements and relationships in shapes and figures. They are particularly useful in finding the sine, cosine, and tangent of angles in right triangles, which can help determine side lengths, angles, and area. Trigonometric functions can also be used to solve problems involving non-right triangles, circles, and other geometric figures by providing a way to relate angles and side lengths within these shapes. Overall, trigonometric functions play a significant role in solving geometric problems and understanding the properties of various shapes.
What is the relationship between the sine and cosine functions in a right triangle?
In a right triangle, the sine of an angle is equal to the length of the side opposite the angle divided by the length of the hypotenuse, while the cosine of the angle is equal to the length of the side adjacent to the angle divided by the length of the hypotenuse. Therefore, the sine and cosine functions are related by the Pythagorean theorem in a right triangle, as sinē(?) + cosē(?) = 1 for any angle ?.
How do the values of the trigonometric functions vary as the angle changes in the unit circle?
As the angle changes in the unit circle, the values of the sine and cosine functions vary between -1 and 1 based on the position of the point on the circle. The tangent function can vary from negative infinity to positive infinity as the angle approaches certain values. The reciprocal functions, secant, cosecant, and cotangent, exhibit similar variations based on the values of cosine, sine, and tangent respectively. Overall, the values of trigonometric functions change continuously as the angle moves around the unit circle.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.
Comments