Transformations Worksheets 8th Grade

Transformations worksheets are a valuable tool for 8th-grade students to reinforce their understanding of geometric transformations. These worksheets provide practice in identifying and applying transformations such as rotations, reflections, translations, and dilations. By engaging with these worksheets, students can develop their spatial reasoning skills and deepen their understanding of how shapes and figures can change in size, position, and orientation.

  Geometry Rotations Worksheet

---

  Geometry Translation Reflection Rotation Worksheets

---

  Transformation 8th Grade Math Worksheets

---

  8th Grade Dilations Worksheet

---

  Translation Math Worksheets

---

  Transformation Geometry Worksheets 8th Grade

---

  Transformation 8th Grade Math Worksheets

---

  8th Grade Math Dilations Worksheets

---

  Transformation Worksheets

---

  Rotation Worksheet 8th Grade Math

---

  Middle School Science Worksheets

---

  8th Grade Energy Worksheets

---

  Dilation Math Worksheets

---

What are transformations?

Transformations are operations that change the position, shape, or size of an object without changing its underlying structure. They include translations (shifting an object's position), reflections (flipping an object across a line), rotations (turning an object around a fixed point), and dilations (changing an object's size while maintaining its shape). Transformations are fundamental concepts in mathematics, computer graphics, and various other fields.

How are translations defined in transformations?

Translations in transformations involve moving all points of an object a certain distance in a specified direction. This involves shifting the entire object in a consistent manner, while keeping its shape, size, and orientation the same. The translation is described by a vector that indicates the direction and distance of the movement.

Explain the concept of reflections in transformations.

In geometry, reflections are a type of transformation that involves flipping an object over a line to create a mirror image. This line is called the line of reflection, and the reflection preserves the size and shape of the object while changing its orientation. The reflection produces a symmetrical image of the original object across the line of reflection, with corresponding points at equal distances from the line. Reflections are one of the fundamental transformations in geometry and are often used to study symmetry and manipulate shapes and figures.

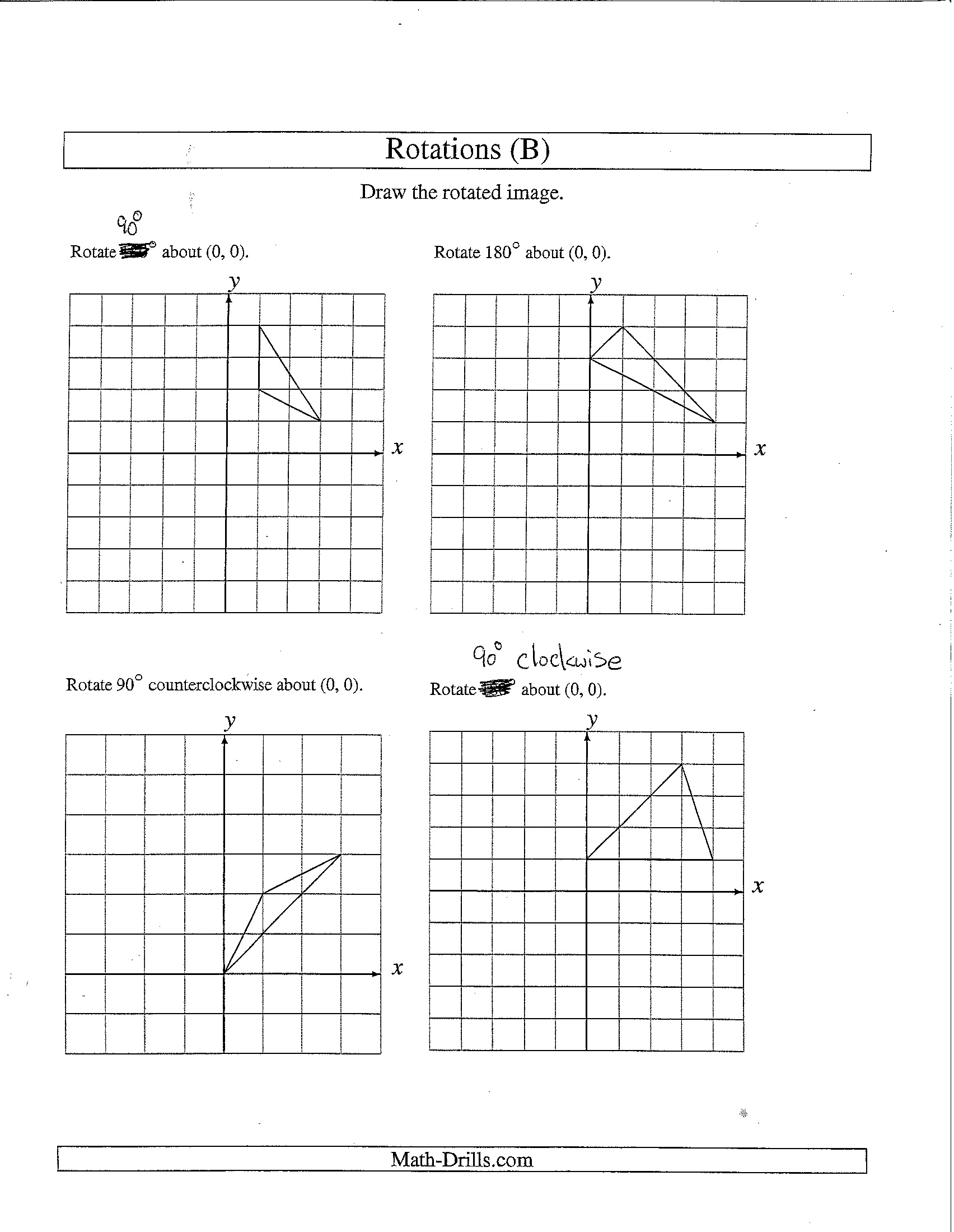
Describe rotational transformations and their characteristics.

Rotational transformations are operations that rotate an object around a fixed point called the center of rotation. These transformations preserve the distance between points on the object and the center and hence do not change the shape or size of the object. The characteristics of rotational transformations include the angle of rotation, the direction of rotation (clockwise or counterclockwise), and the center of rotation. Rotational transformations are typically described using angles in degrees or radians, and the properties of these transformations make them useful in various applications such as graphics, physics, and engineering.

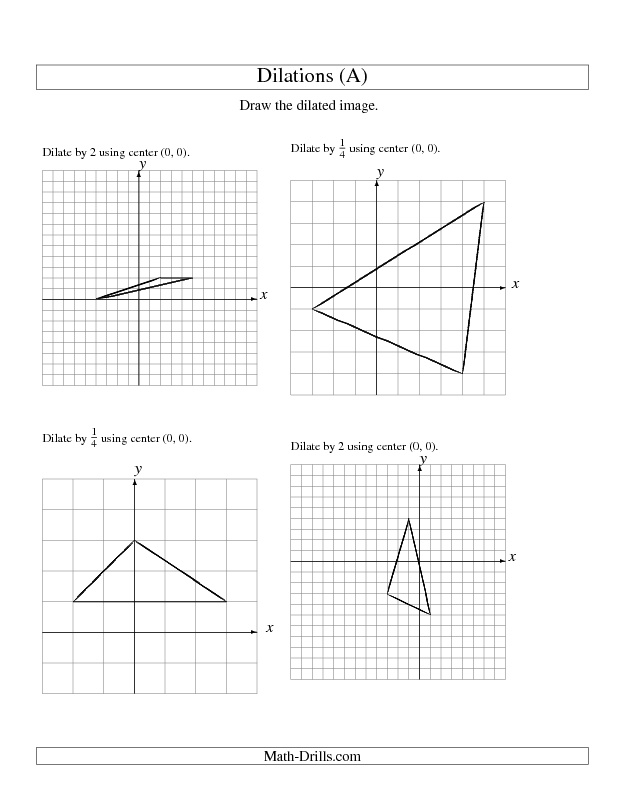
How are dilations used in transformations?

Dilations are used in transformations to scale an object up or down by a specific factor while preserving its shape. This type of transformation involves multiplying the coordinates of the object by the dilation factor, causing it to expand or shrink in size. Dilations can be used to create similar figures, enlarge or reduce images, or generate patterns with proportional relationships in geometry and art.

What is the difference between rigid and non-rigid transformations?

Rigid transformations, also known as isometries, are transformations that preserve both the shape and size of an object, such as translations, rotations, and reflections. In contrast, non-rigid transformations change the shape or size of an object, such as scaling or stretching. Rigid transformations maintain the distance between points, while non-rigid transformations do not necessarily preserve these distances.

How can the properties of shapes change through transformations?

The properties of shapes can change through transformations such as translations, rotations, reflections, and dilations. Translations shift the shape without changing its size or orientation, rotations change the orientation of the shape, reflections produce mirror images, and dilations resize the shape while maintaining its proportions. These transformations can impact various properties of the shape, including its size, orientation, position, and symmetry.

What are the different types of symmetry in transformations?

The different types of symmetry in transformations include reflectional symmetry, rotational symmetry, translational symmetry, and glide reflection symmetry. Reflectional symmetry occurs when a shape can be reflected over a line and still remain unchanged. Rotational symmetry occurs when a shape can be rotated around a point and still look the same in different positions. Translational symmetry involves moving a shape in a certain direction while still maintaining its original form. Glide reflection symmetry combines both reflection and translation, where a shape is reflected across a line and then translated along that line.

How is the concept of congruence related to transformations?

Congruence is related to transformations in geometry as transformations such as translations, rotations, reflections, and dilations can all preserve the congruence of geometric figures. When two figures are congruent, it means they have the same shape and size. By applying different transformations to geometric figures, it is possible to change their position, orientation, or size while still maintaining their congruence. In other words, congruence is a fundamental property that remains unchanged under certain transformations.

What real-life examples can you think of that involve transformations?

Real-life examples of transformations include a caterpillar transforming into a butterfly, a person undergoing a physical or fitness transformation through exercise and healthy eating, a city undergoing a revitalization project to improve infrastructure and aesthetics, and a company transforming its business model to adapt to market changes such as shifting to online sales. Each of these examples involve a significant change or improvement over time, resulting in a transformed outcome.