Transformations of Functions Worksheets

Transformations of Functions Worksheets are an essential tool for learners who want to deepen their understanding of how functions can be modified or transformed. These worksheets provide valuable practice and reinforce concepts such as translation, reflection, stretching, and compression. By working through these exercises, students can sharpen their skills and develop a solid grasp of the different ways in which functions can be manipulated.

  Parent Functions Graphs Worksheet

---

  Function Transformation Worksheet

---

  Exponents

---

  Write Each Line From the Equation Worksheet

---

  Quadratic Formula Discriminant Worksheet

---

  Absolute Value Inequalities Worksheets

---

  Basic Trig Functions Worksheet

---

  Basic Logarithm Worksheet

---

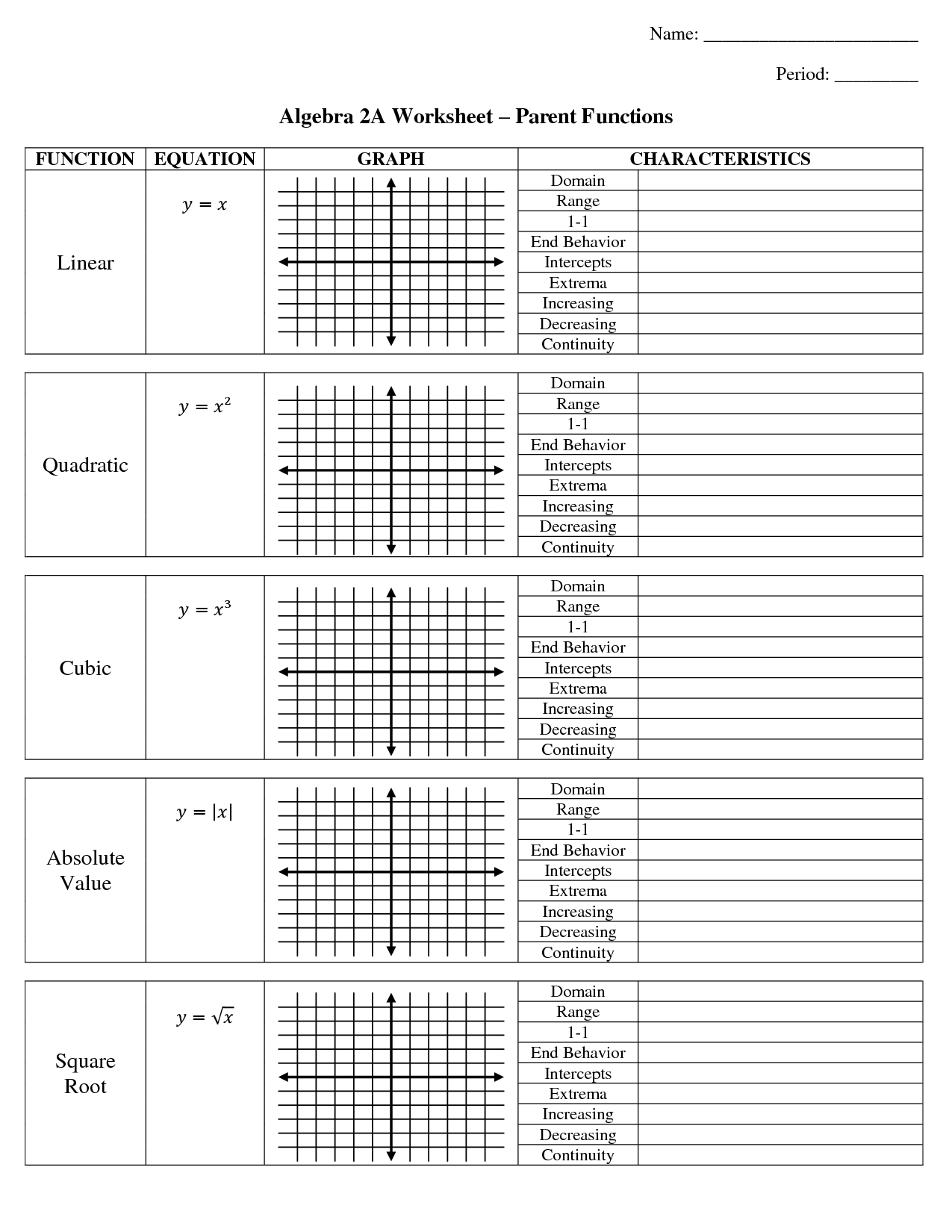
What are the different types of transformations that can be applied to a function?

There are several types of transformations that can be applied to a function, including translation (shifting the function up, down, left, or right), dilation (stretching or compressing the function vertically or horizontally), reflection (flipping the function over an axis), and rotation (changing the orientation of the function around a fixed point). These transformations can help modify the shape, position, and size of the original function to create different variations and visual representations.

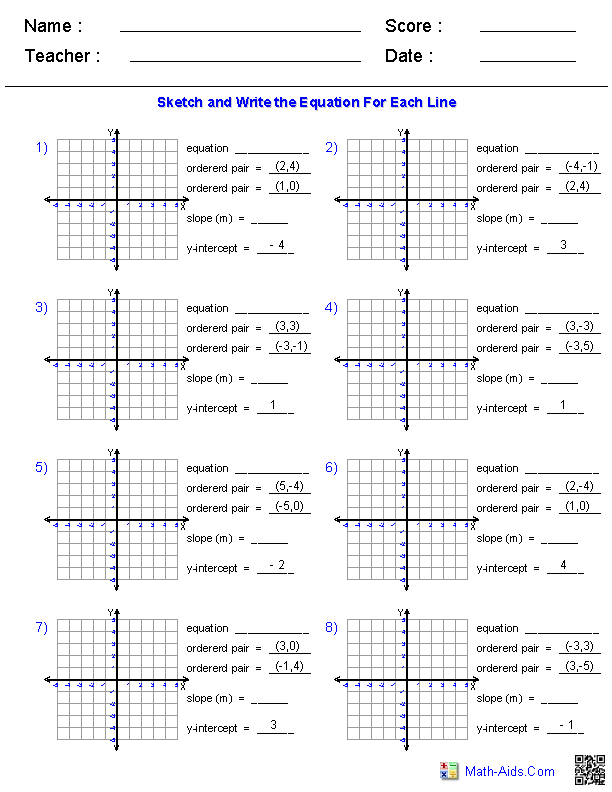
How do you describe the horizontal translation of a function?

The horizontal translation of a function refers to shifting the graph of the function horizontally along the x-axis. If the function is shifted to the right, the translation is positive, and if it is shifted to the left, the translation is negative. This movement changes the location of the function's graph without altering its shape or orientation.

What happens to a function when it undergoes a vertical translation?

When a function undergoes a vertical translation, it shifts upward or downward on the coordinate plane but maintains the same shape. This means that the y-values of the function are increased or decreased uniformly by a certain amount, without affecting the x-values. The general form of a vertically translated function is f(x) + c, where c represents the amount of vertical shift.

How does a function change when it undergoes a reflection across the x-axis?

When a function undergoes a reflection across the x-axis, the y-values of the function are negated. In other words, each positive y-value becomes negative and each negative y-value becomes positive. The shape of the graph remains the same, but the orientation is flipped upside down with respect to the x-axis.

What is the effect of a reflection across the y-axis on a function?

A reflection across the y-axis of a function results in the transformation where each point (x, y) on the original function is mapped to the point (-x, y) on the reflected function. This means that the x-coordinates of all points are negated, leading to a mirrored image of the original function across the y-axis. The shape of the function remains the same, but it is flipped horizontally.

How do you describe the vertical stretch or compression of a function?

The vertical stretch/compression of a function refers to the action of changing the vertical size of the graph of the function. A vertical stretch occurs when the function is multiplied by a number greater than 1, stretching the graph vertically. Conversely, a vertical compression happens when the function is multiplied by a fraction between 0 and 1, compressing the graph vertically. The stretch/compression factor affects the amplitude of the function's graph, making it narrower or taller depending on the value of the factor.

What happens to a function when it undergoes a horizontal stretch or compression?

When a function undergoes a horizontal stretch, it results in the function being stretched horizontally, causing it to be wider than the original function. On the other hand, a horizontal compression causes the function to be compressed horizontally, making it narrower than the original function. Both operations affect the shape and position of the function on the graph, but do not change its vertical position.

How does the function change when it is vertically stretched or compressed and reflected across the x-axis?

When a function is vertically stretched or compressed, the distance between the function and the x-axis is changed by a factor determined by the stretch/compression factor. When the function is reflected across the x-axis, the positive values become negative and negative values become positive, effectively mirroring the function across the x-axis.

What is the combined effect of a horizontal translation and a vertical stretch on a function?

A horizontal translation shifts the function left or right along the x-axis, while a vertical stretch affects the vertical values of the function making it narrower or wider. When combined, the horizontal translation alters the position of the function while the vertical stretch changes the height of the function. The overall effect is a transformation that shifts and stretches the function simultaneously in the x and y directions.

How does a function transform when it undergoes multiple transformations simultaneously?

A function will undergo multiple transformations simultaneously by applying each transformation to the original function in sequence. For example, if a function is translated, and then scaled, both transformations will be applied in order to the original function. Each transformation will affect the function based on its specific rule, such as shifting it horizontally or vertically, or stretching/compressing it. The final result will be a function that has undergone all the specified transformations simultaneously.