Transformation Worksheets Geometry

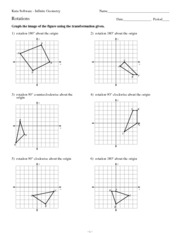
Transformation worksheets in geometry are a valuable tool for students to practice and reinforce their understanding of geometric concepts. These worksheets focus on various types of transformations, such as translations, rotations, reflections, and dilations. With clear instructions and a variety of practice problems, these worksheets help students solidify their understanding of how shapes can be altered in space. Whether you are a teacher looking for additional resources or a student seeking extra practice, these transformation worksheets are an excellent resource to enhance your learning experience.

  7th Grade Math Worksheets

---

  Geometry Translations Worksheet

---

  Geometry Slide Flip Turn Worksheets

---

  Geometry Reflection Worksheet

---

  Tangent Worksheet with Answers

---

  Math Reflection Examples

---

  Kuta Software Transformations Worksheets

---

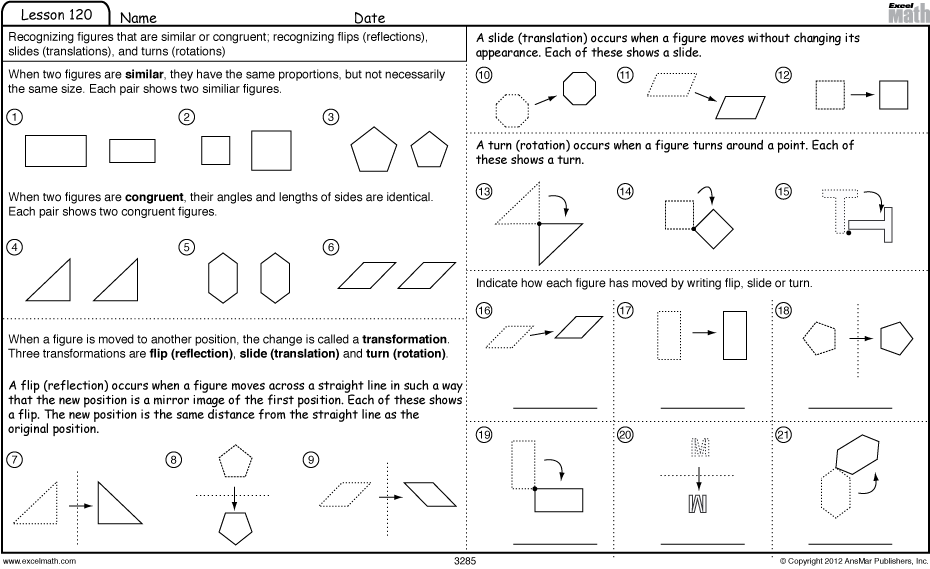
What is a transformation in geometry?

In geometry, a transformation refers to changing the position, size, or shape of a figure. Common transformations include translations (sliding), rotations (turning), reflections (flipping), and dilations (resizing). These transformations help to visualize and understand the relationships between different geometric figures and their properties.

What are the four types of transformations?

There are four main types of transformations: translation, rotation, reflection, and dilation. Translation moves an object without changing its shape or size, rotation involves turning an object around a fixed point, reflection flips an object over a line to create a mirror image, and dilation involves stretching or shrinking an object while maintaining its shape.

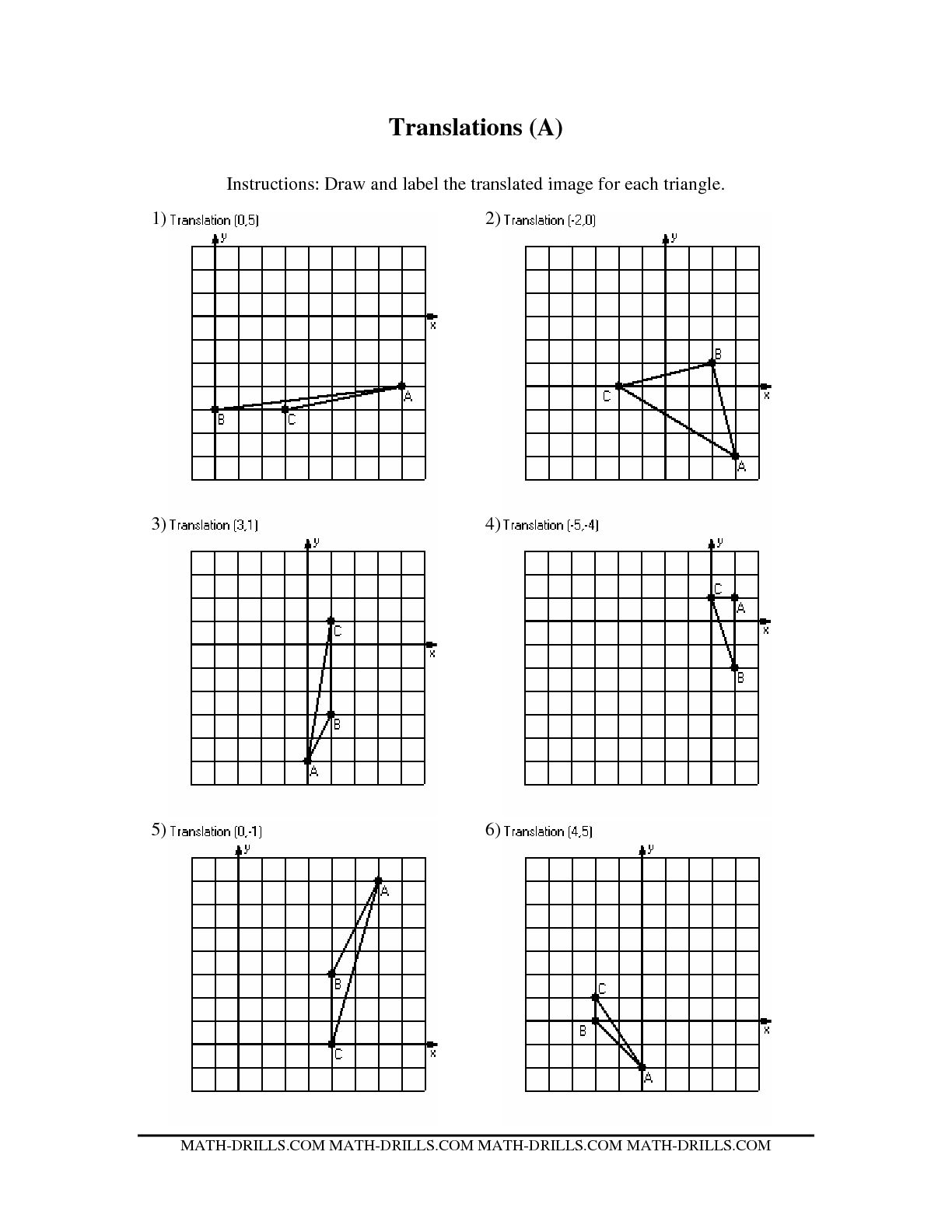
Describe a translation transformation.

A translation transformation in mathematics refers to moving an object from one position to another without rotation, reflection, or resizing. This is done by shifting every point of the object by the same amount in a specified direction. The object remains the same size and shape, just appears in a different location.

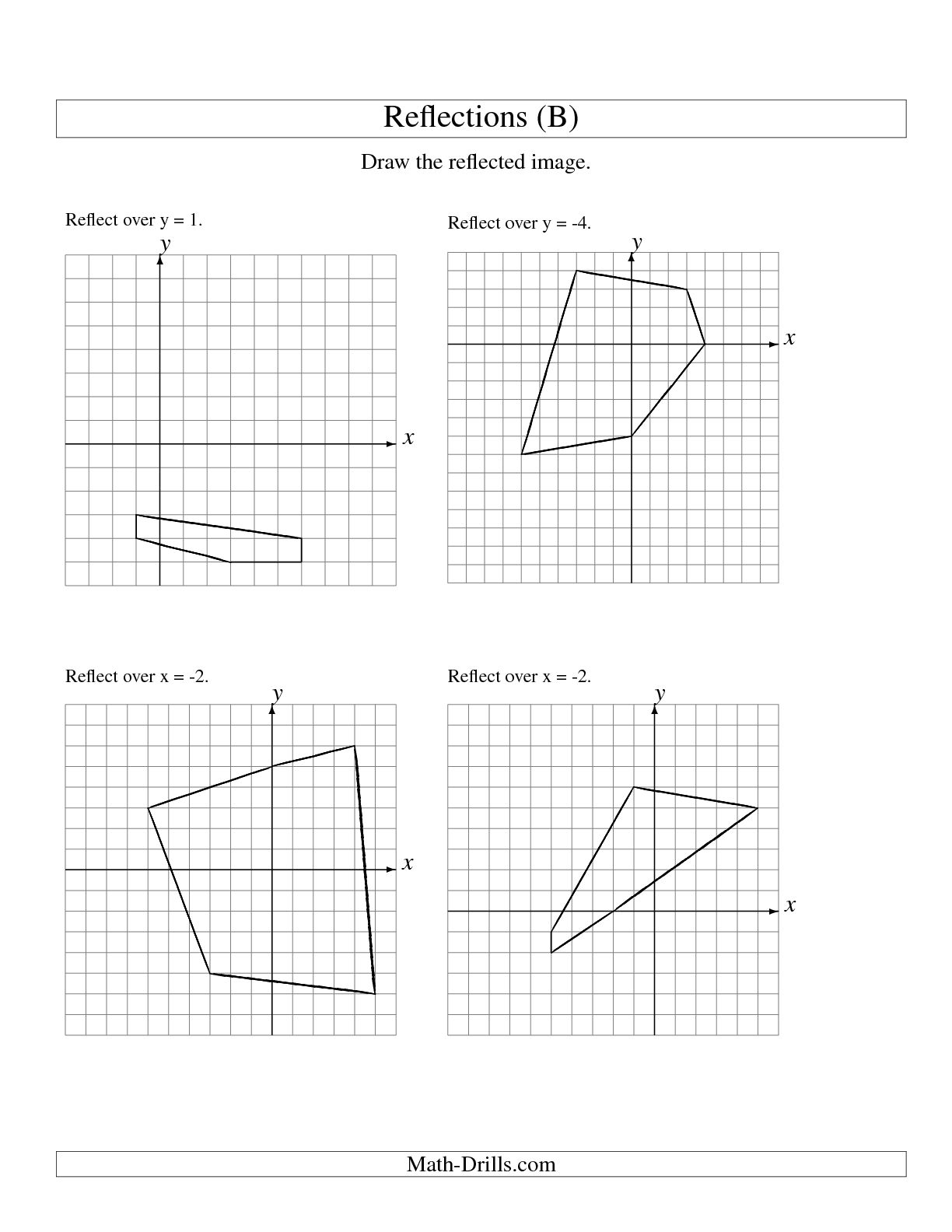
What is a reflection transformation?

A reflection transformation is a type of transformation in geometry where a figure is flipped over a line called the axis of reflection, resulting in a mirror image of the original figure. This transformation is also known as a flip or a mirror image, and it preserves the size and shape of the object being reflected.

Explain a rotation transformation.

A rotation transformation is a linear transformation that involves rotating an object or shape around a fixed point called the center of rotation by a specific angle. This transformation preserves the shape and size of the object but changes its orientation. The angle and direction of the rotation determine the new position of the object after the transformation. Rotation transformations are commonly used in computer graphics, animation, and geometric calculations to manipulate and modify objects in a virtual space.

Describe a dilation transformation.

A dilation transformation is a type of transformation that enlarges or shrinks an object without changing its shape. It is characterized by a scale factor, which determines the amount of enlargement or reduction. The object is dilated from a fixed point called the center of dilation, with all points on the object moving away from or towards the center by the same scale factor. This results in the object appearing either larger or smaller but maintaining its proportionality to the original figure.

What is the difference between a rigid transformation and a non-rigid transformation?

A rigid transformation is a transformation that preserves distances and angles between points, such as translations, rotations, and reflections. In contrast, a non-rigid transformation does not preserve distances and angles, and can involve scaling, stretching, or deforming an object. This means that rigid transformations maintain the shape and size of an object, while non-rigid transformations can change the shape and size of an object.

How are transformations represented in coordinate notation?

Transformations in coordinate notation are represented using specific rules and formulas to describe how the points in a figure are shifted, rotated, reflected, or resized. For example, translations are represented as (x + a, y + b) where a represents the horizontal shift and b represents the vertical shift, rotations are represented as (x cos ? - y sin ?, x sin ? + y cos ?) where ? represents the angle of rotation, and reflections are represented as (±x, ±y) based on the axis of reflection. Scaling transformations are represented as (kx, ky), where k represents the scale factor. These notations help accurately describe the changes in position, orientation, and size of geometric figures in a coordinate plane.

What is the importance of transformations in geometry?

Transformations in geometry are important as they allow us to visualize and understand how shapes can change while still maintaining their fundamental properties. By applying transformations such as rotations, reflections, translations, and dilations, we can analyze patterns, symmetries, and congruence in geometric figures. These transformations also play a crucial role in solving problems related to symmetry, congruence, and similarity, as well as in areas like computer graphics, architecture, and design. Overall, mastering transformations enhances our ability to manipulate and analyze geometric shapes effectively.

How can you determine the properties of a transformed figure using transformation worksheets?

By completing transformation worksheets, you can determine the properties of a transformed figure by analyzing how the original shape has been translated, rotated, reflected, or dilated. You can use the coordinates of the vertices to calculate the new position of the shape after the transformation, and then identify any changes in size, orientation, or symmetry. The worksheets typically provide guided exercises that help you understand how different transformations affect the properties of geometric figures, allowing you to develop a deeper understanding of spatial relationships and mathematical concepts.