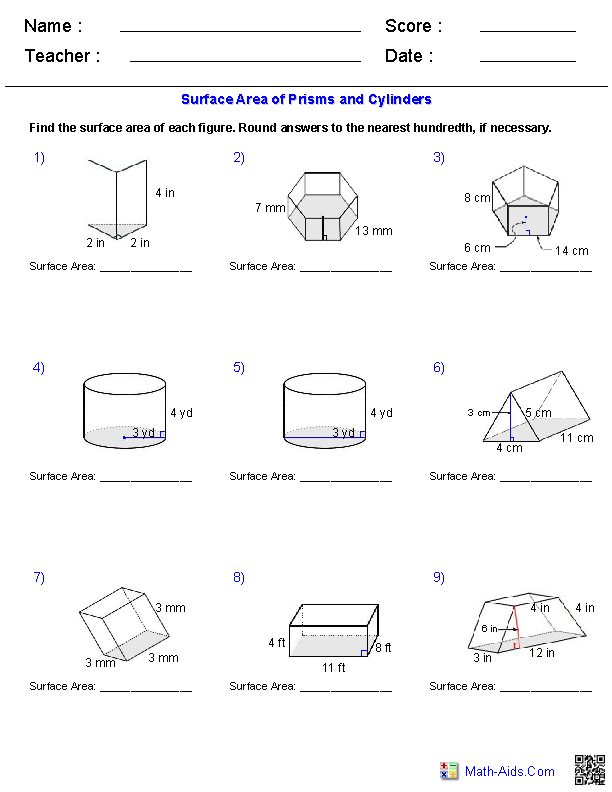
Surface Area of Prisms and Cylinders Worksheet

If you are a middle or high school student studying geometry, you may find yourself needing practice with calculating the surface area of prisms and cylinders. These complex figures involve multiple sides and curved surfaces, making it important to understand the concepts and formulas involved. In order to solidify your understanding and improve your proficiency, a surface area of prisms and cylinders worksheet can be a valuable tool. Such a worksheet provides a range of problems and exercises that allow you to practice and reinforce your knowledge of these geometric entities and their associated subjects.

  Surface Area and Volume of Cones Worksheets

---

  Geometry Surface Area and Volume Worksheets

---

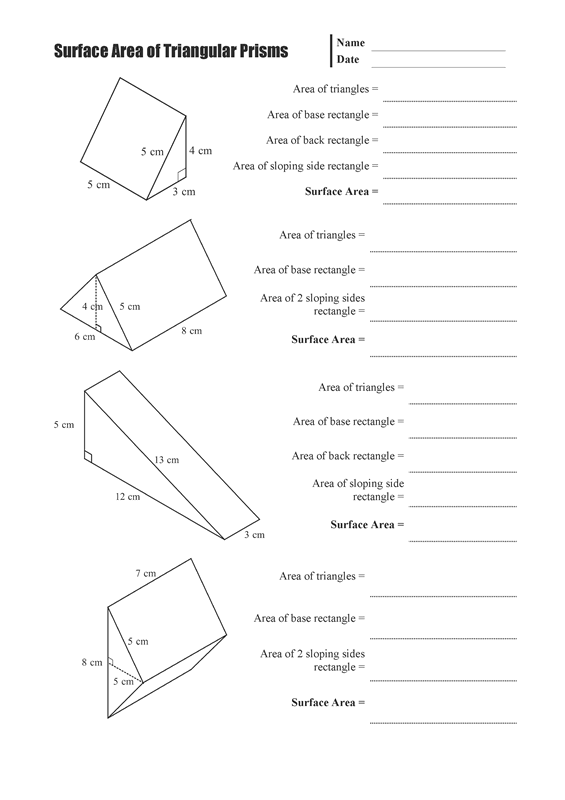
  Triangular Prism Surface Area Worksheet

---

  Triangular Prism Surface Area Worksheet

---

  Rectangular Prism Surface Area Worksheet

---

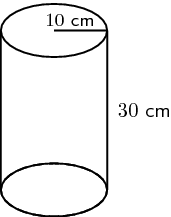
  Cylinder Surface Area Example

---

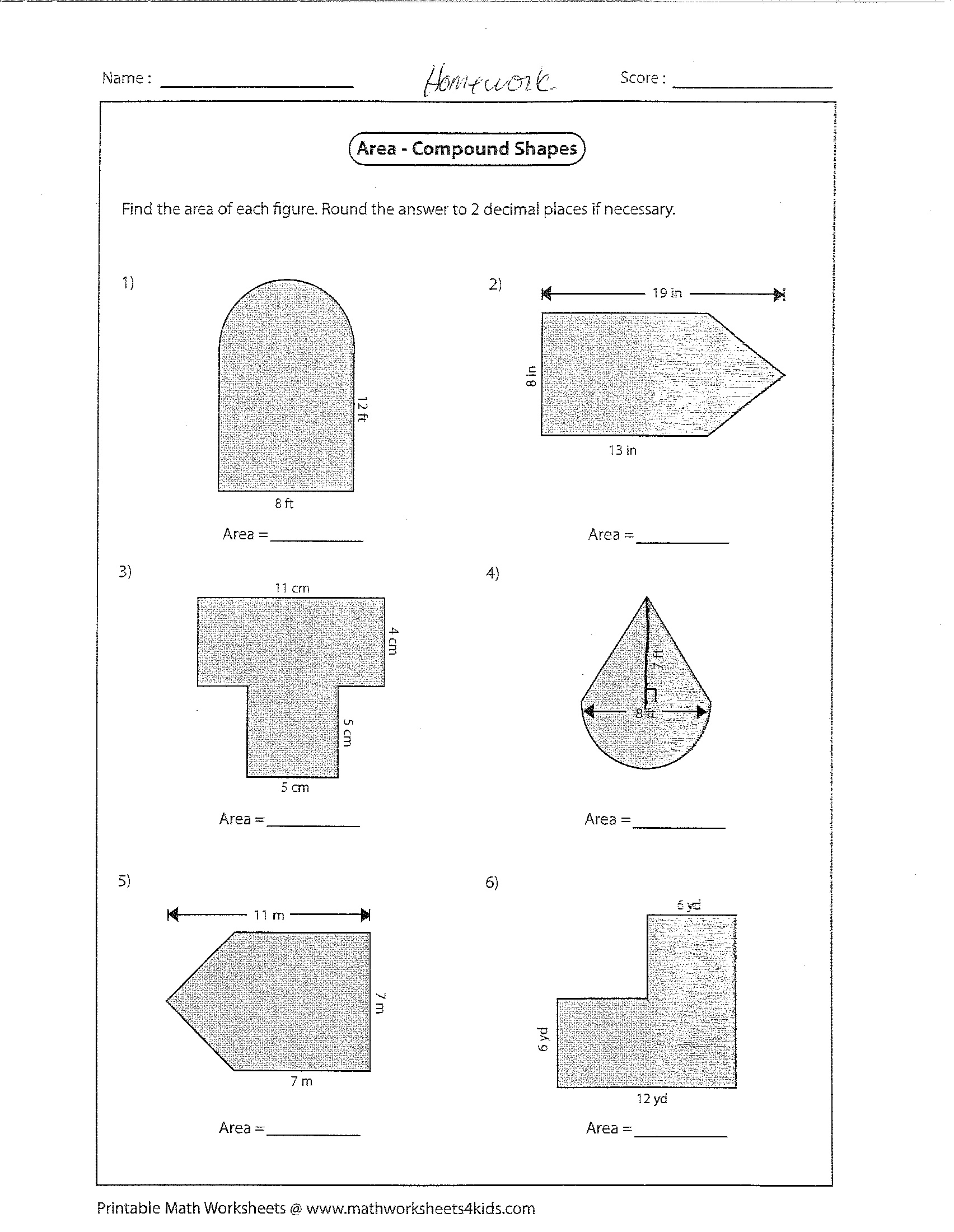
  Composite Figures Area Worksheet

---

  Triangular Prism

---

  Calculating Area and Perimeter

---

  Volume Pyramids Cones Spheres Worksheet

---

What is the formula for finding the surface area of a rectangular prism?

The formula for finding the surface area of a rectangular prism is 2(LW + WH + LH), where L is the length, W is the width, and H is the height of the prism.

How do you calculate the surface area of a triangular prism?

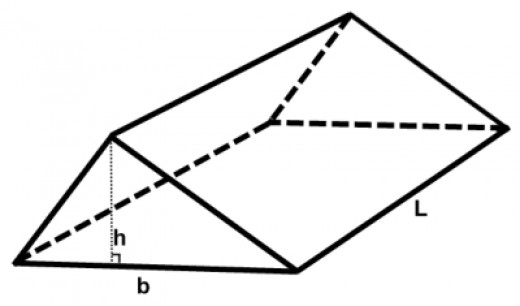
To calculate the surface area of a triangular prism, you need to find the area of all its surfaces and then add them together. The formula for the surface area of a triangular prism is SA = 2*(base area of the triangle) + (perimeter of the triangle)*(height of the prism). First, calculate the area of the triangular base using the base and height of the triangle. Then, find the perimeter of the triangle by adding up the lengths of its three sides. Finally, multiply the perimeter of the triangle by the height of the prism and add 2 times the base area to get the total surface area of the triangular prism.

What is the formula for finding the surface area of a cylinder?

The formula for finding the surface area of a cylinder is 2?r(r+h), where r is the radius of the base of the cylinder and h is the height of the cylinder.

How do you calculate the surface area of a cone?

To calculate the surface area of a cone, you need to add the area of the base (which is a circle) to the area of the curved surface. The formula for the total surface area of a cone is ?r(r + l), where r is the radius of the base and l is the slant height of the cone (the distance from the apex to the base). Add the area of the base (?r^2) to the curved surface area (?rl) to get the total surface area of the cone.

Can the surface area of a prism or cylinder ever be negative?

No, the surface area of a prism or cylinder can never be negative. Surface area is a measurement of the total area of all the surfaces of a three-dimensional solid, and it is always a non-negative value as it cannot have a negative physical significance.

How does increasing the dimensions of a prism or cylinder affect its surface area?

Increasing the dimensions of a prism or cylinder will directly increase its surface area. The surface area of a prism or cylinder is determined by the formula 2?rh + 2?r^2 for a cylinder, and for a prism, it is the sum of the areas of all its faces. As the dimensions, such as height and radius for a cylinder, or length, width, and height for a prism, increase, the surface area will increase as well since more surfaces are being added or expanded.

What does the surface area represent in the context of a prism or cylinder?

In the context of a prism or cylinder, the surface area represents the total area of all the faces that make up the shape. This includes the lateral or curved surface area, as well as the areas of the bases. The surface area is important for calculating how much material is needed to cover or paint the shape, and it is also useful for determining heat transfer or other applications where surface area plays a role.

Is the surface area of a cylinder always greater than that of a prism with the same base and height?

No, the surface area of a cylinder is not always greater than that of a prism with the same base and height. The surface area of a prism is calculated by adding the areas of all its faces, while the surface area of a cylinder is calculated by adding the areas of its two circular bases and its lateral surface area. Depending on the dimensions and proportions of the cylinder and prism, the surface area of the prism could potentially be greater than that of the cylinder.

How do you calculate the surface area of a sphere?

To calculate the surface area of a sphere, you use the formula A = 4?r^2, where A is the surface area and r is the radius of the sphere. Simply square the radius, multiply it by 4, and then multiply that result by ? (pi), which is approximately 3.14159. This formula will give you the total surface area of the sphere.

What are some real-world applications of calculating surface area for prisms and cylinders?

Calculating surface area for prisms and cylinders is crucial in various real-world applications such as construction and architecture for determining the amount of materials needed like paint or wallpaper, in manufacturing for estimating the packaging or wrapping materials required, in engineering for designing pipelines or containers, and in the medical field for determining the surface area of organs for drug dosing calculations. Additionally, in everyday scenarios, understanding surface area helps with tasks like wrapping gifts or calculating the amount of fabric needed for sewing projects.