Surface Area Cylinder Worksheet
Are you in need of a practical and comprehensive worksheet that will help you understand the concept of surface area for cylinders? Look no further! This worksheet is specifically designed for students seeking to deepen their knowledge of this mathematical entity. With clear and concise instructions, this worksheet will guide you through various exercises and calculations, ensuring a thorough understanding of the subject.
Table of Images 👆
- 8th Grade Math Practice Worksheets
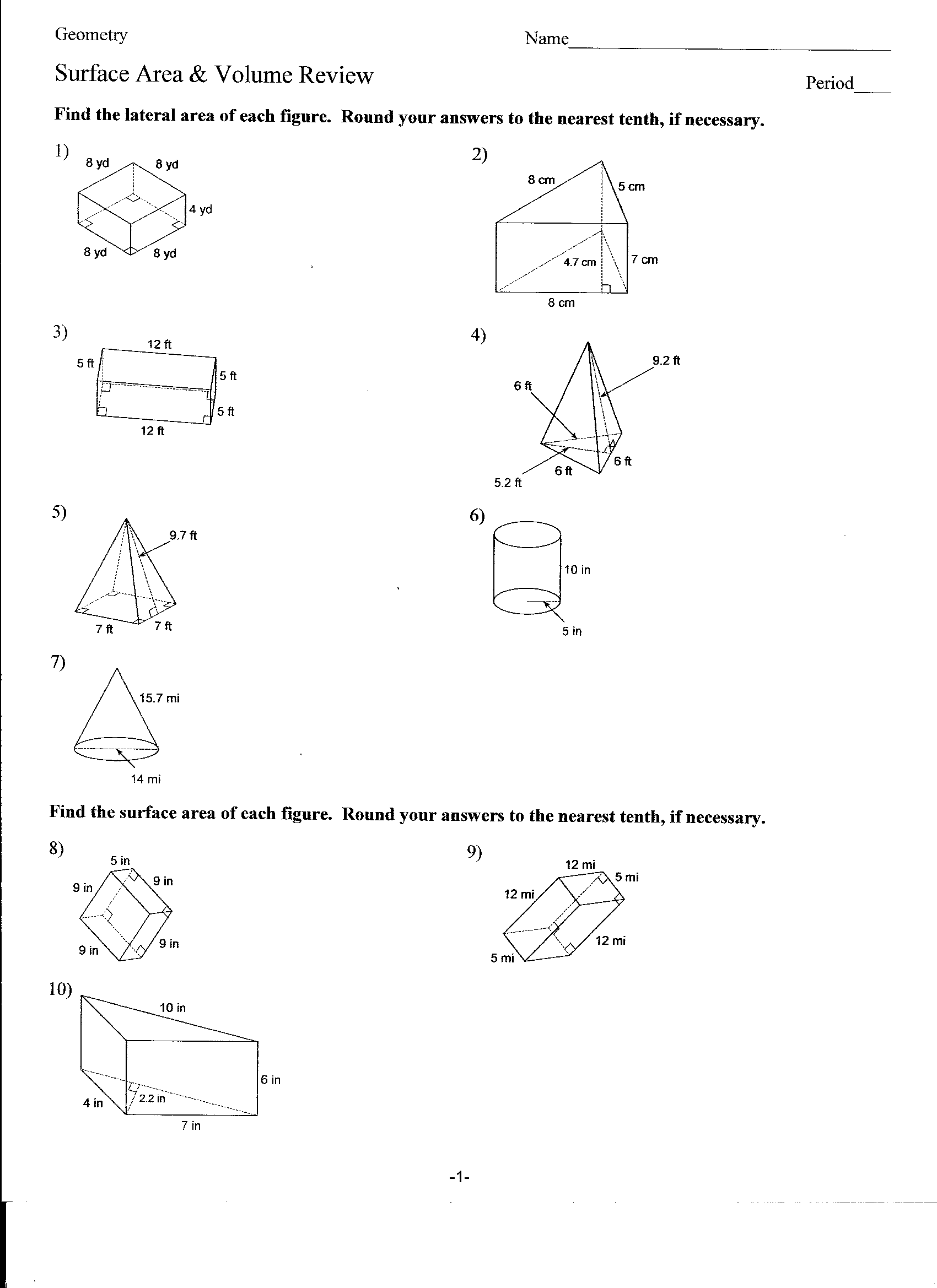
- Surface Area and Volume Worksheets
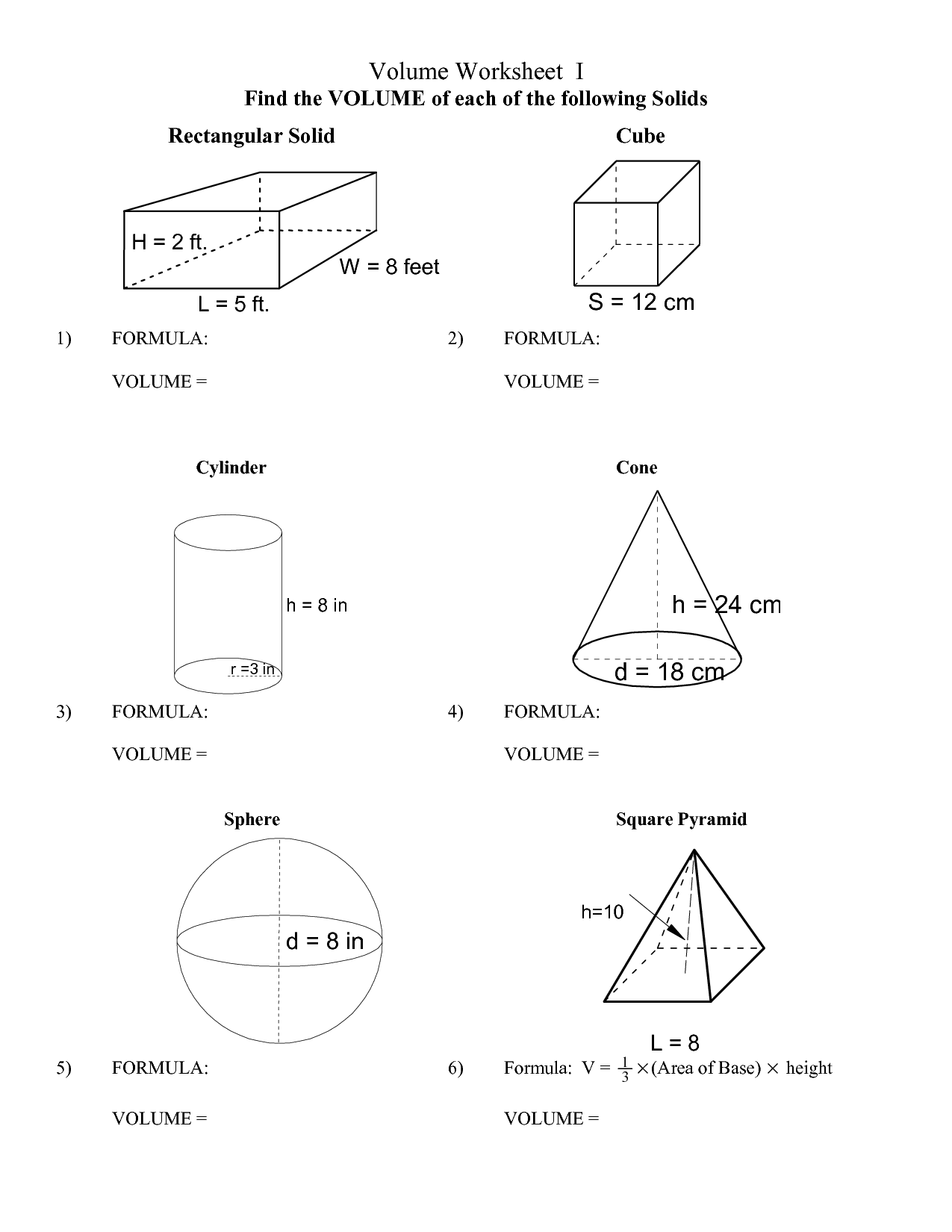
- Volume Pyramid Worksheet
- 7th Grade Math Worksheets
- How to Find Perimeter of Cone
- Surface Area and Volume Worksheets
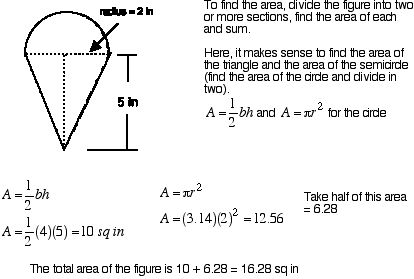
- Lateral Surface Area of a Cone
- 8th Grade Math Worksheets
- Geometry Vocabulary Crossword Puzzle
- Pentagonal Prism Net
- Triangular Pyramid Surface Area Formula
- Triangular Prism Surface Area Worksheet
- Printable Cube Nets
- 3D Cylinder Geometric Shape
- 3D Shape Nets
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
What is the formula for finding the surface area of a cylinder?
The formula for finding the surface area of a cylinder is 2πr^2 + 2πrh, where r is the radius of the circular base and h is the height of the cylinder.
Explain how to calculate the surface area of a cylinder when given the height and radius.
To calculate the surface area of a cylinder, use the formula: 2πrh + 2πr^2, where "r" is the radius and "h" is the height of the cylinder. First, multiply the radius (r) by the height (h) and then multiply by 2π. Next, calculate the area of the two circular bases by multiplying 2πr^2. Finally, add the two results together to get the total surface area of the cylinder.
Can the surface area of a cylinder be greater than its volume? Why or why not?
Yes, the surface area of a cylinder can be greater than its volume. This is because the surface area of a cylinder is determined by the sum of its lateral surface area and the two circular bases, while the volume is dependent on the product of the base area and height. A cylinder with a small height and large radius can have a greater surface area than volume, as the lateral surface area and base areas contribute more to the total surface area than the volume calculation.
Describe the relationship between the surface area and volume of a cylinder.
The relationship between the surface area and volume of a cylinder is such that as the volume of the cylinder increases, its surface area also increases. This is because the surface area of a cylinder is directly proportional to its volume. As the cylinder grows in size, its surface area must also increase in order to maintain a proportional relationship with its volume. Conversely, if the volume of the cylinder decreases, its surface area will also decrease.
If the radius of a cylinder is doubled, what happens to its surface area?
If the radius of a cylinder is doubled, its surface area will increase by a factor of four. This is because the surface area formula for a cylinder is 2πr^2 + 2πrh, where r is the radius and h is the height of the cylinder. When the radius is doubled, the new surface area will be 2π(2r)^2 + 2π(2r)h, which simplifies to 4(2πr^2 + πrh), resulting in a fourfold increase in surface area.
How would the surface area change if the height of a cylinder is cut in half?
If the height of a cylinder is cut in half, the surface area would also be halved. This is because the surface area of a cylinder is dependent on both the height and radius of the cylinder. Cutting the height in half would reduce the surface area proportionally.
What would happen to the surface area if a section of the cylinder is cut and removed?
If a section of the cylinder is cut and removed, the surface area of the cylinder would decrease. This is because the removed section of the cylinder contributes to the total surface area of the shape, so its absence would result in a reduction in the overall surface area of the cylinder.
If the radius is halved and the height is doubled, what effect does it have on the surface area?
Halving the radius and doubling the height of a cylinder results in a decrease in surface area. The surface area of a cylinder is given by the formula 2πr(r + h), where r is the radius and h is the height. When the radius is halved, the first term (2πr) decreases, and when the height is doubled, the second term (r + h) increases. However, since the radius term has a greater impact on the surface area, the overall effect is a reduction in surface area.
What does the surface area of a cylinder represent in real-world applications?
The surface area of a cylinder represents the amount of material needed to cover the outside of the cylinder. In real-world applications, this can be important for determining the amount of paint needed to cover a cylindrical storage tank, the amount of fabric needed to wrap a cylindrical gift, or the amount of insulation needed to cover a cylindrical pipe in a building.
Can a cylinder have the same surface area but different dimensions?
Yes, it is possible for a cylinder to have the same surface area but different dimensions. This is because there are infinite combinations of height and radius that can result in the same total surface area for a cylinder. As long as the formula for calculating the surface area (2πrh + 2πr^2) results in the same value, the cylinder can have different dimensions.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.






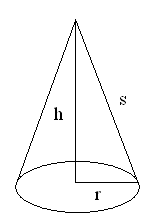


















Comments