Subsets of Real Numbers Worksheet

Are you a math enthusiast or a student looking to deepen your understanding of subsets of real numbers? If so, this blog post is for you. In this article, we will explore the concept of subsets of real numbers and how they relate to different entities and subjects in mathematics. Whether you're studying for a math exam, preparing for a math competition, or simply looking for additional practice, this worksheet will provide you with the perfect opportunity to enhance your skills and comprehension in this area of math.

  Real Number System Chart

---

  Rational Numbers Examples

---

  Properties of Real Numbers Examples

---

  Real Number System Graphic Organizer

---

  Real Number System Worksheets

---

  Math Numbers Operations Worksheets

---

  Real Number System Worksheets

---

  Adding and Subtracting Real Numbers Worksheet

---

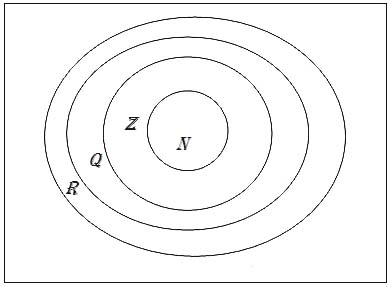
  Sets of Real Numbers Venn Diagram

---

  Triangles and Their Properties

---

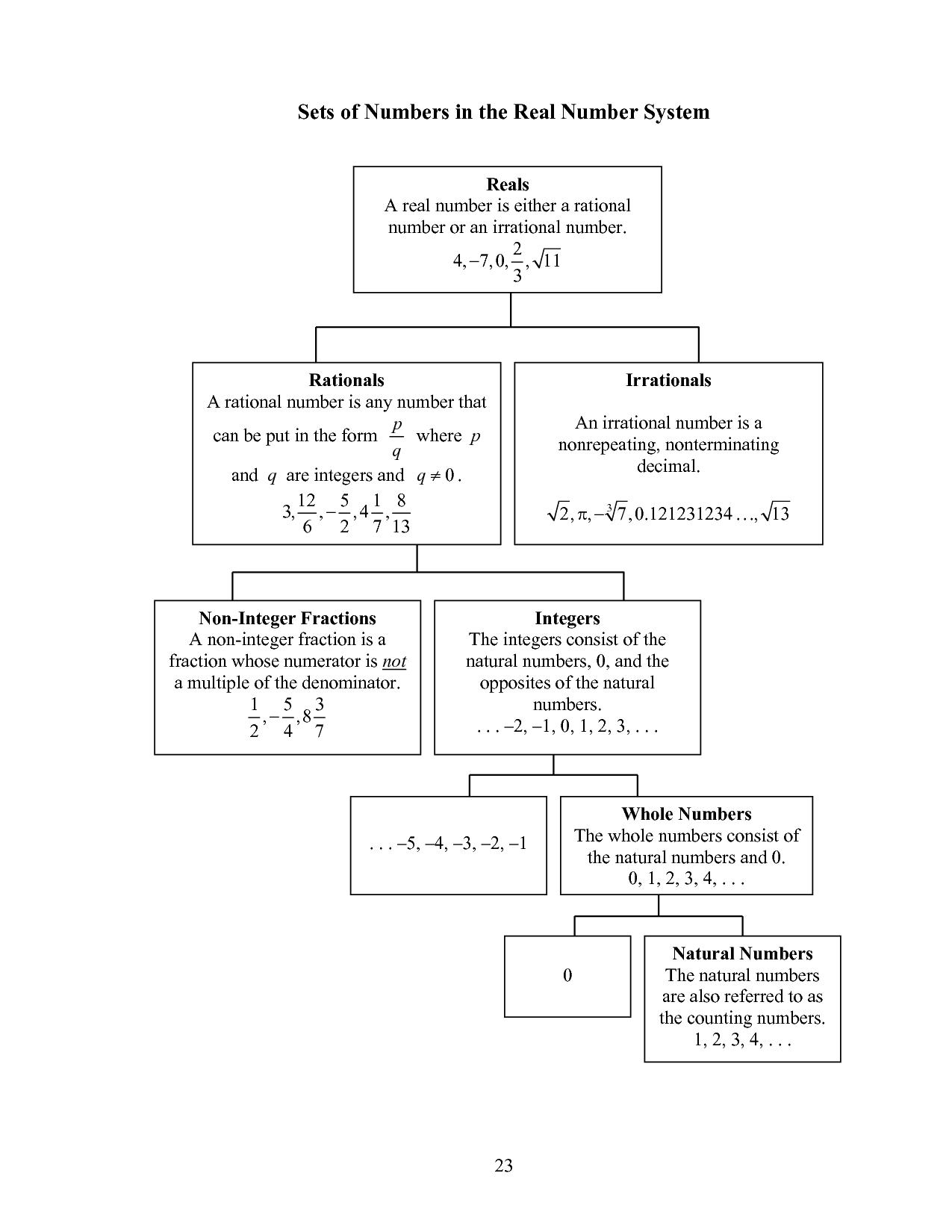
What are subsets of real numbers?

Subsets of real numbers are sets that contain only certain elements of the real number system, such as integers, rational numbers, irrational numbers, and so on. These subsets can be classified based on their properties, such as whether they are bounded or unbounded, discrete or continuous, finite or infinite, and so forth. Examples of subsets of real numbers include natural numbers, whole numbers, even numbers, odd numbers, prime numbers, and more.

How are subsets of real numbers different from the entire set of real numbers?

Subsets of real numbers are specific groupings of numbers taken from the entire set of real numbers, while the entire set of real numbers includes all possible numbers without any omissions. Subsets are smaller and more limited in scope compared to the infinite set of real numbers, which encompasses all possible values along the number line, both rational and irrational.

Give an example of a proper subset of real numbers.

An example of a proper subset of real numbers could be the set of all positive real numbers, denoted as \( \mathbb{R}^+ \). This subset contains all real numbers that are greater than zero, but it excludes zero and all negative real numbers.

Can the set of natural numbers be considered a subset of real numbers?

Yes, the set of natural numbers can be considered a subset of real numbers since every natural number is also a real number. The natural numbers are a subset of the real numbers as they are a specific subset that includes all positive integers starting from 1.

How does the empty set relate to subsets of real numbers?

The empty set is a subset of any set, including the set of real numbers. In other words, the empty set is a subset of the real numbers because it does not contain any elements and every set, including the real numbers, contains the empty set as a subset.

Are irrational numbers a subset of real numbers?

Yes, irrational numbers are a subset of real numbers. Real numbers include both rational numbers (numbers that can be expressed as a fraction) and irrational numbers (numbers that cannot be expressed as a fraction). Irrational numbers are a subset of real numbers as they are a part of the broader set of all real numbers.

Provide an example of an infinite subset of real numbers.

One example of an infinite subset of real numbers is the set of all even integers, which can be represented as {..., -4, -2, 0, 2, 4, ...}. This subset is infinite because there is no largest even integer and it continues indefinitely in the positive and negative directions.

Can a set of integers be considered a subset of real numbers?

Yes, a set of integers can be considered a subset of real numbers. In fact, all integers are also real numbers as real numbers encompass a wider range of numbers including integers, rational numbers, irrational numbers, and more. Therefore, every integer is also a real number, making the set of integers a subset of the real numbers.

Are whole numbers a subset of real numbers?

Yes, whole numbers are a subset of real numbers. Real numbers include all rational and irrational numbers, while whole numbers are a subset of natural numbers that are non-negative integers. Therefore, every whole number is also a real number since it falls within the broader category of real numbers.

Give an example of a non-empty finite subset of real numbers.

An example of a non-empty finite subset of real numbers is the set {1, 2, 3, 4, 5}.