Solving Proportions Worksheets 6th Grade
Are you a 6th-grade student looking to practice solving proportions? Look no further! In this blog post, we will explore a variety of worksheets designed specifically for 6th-grade entities who want to develop their skills in solving proportions. Whether you are a student who is struggling with this concept or simply seeking additional practice, these worksheets will provide the necessary materials and guidance to help you succeed.
Table of Images 👆
- 6th Grade Math Worksheets
- Ratio and Proportion Problems
- Solving Ratios and Proportions Worksheets
- 7th Grade Math Problems Worksheets
- 5th Grade Math Worksheets Graphs
- 7th Grade Math Word Problems
- Middle School Math Word Problems
- Grade Preposition Worksheets for Kids
- Solving Two-Step Equations Worksheet
- Proportion Word Problems
- Proportion Word Problems
- Proportion Word Problems
- Proportion Word Problems
- Proportion Word Problems
- Proportion Word Problems
- Proportion Word Problems
- Proportion Word Problems
- Proportion Word Problems
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What is a proportion?
A proportion is a statement that two ratios are equal. In other words, it is a comparison of two quantities that shows they have the same relative size. Proportions are commonly used in mathematics, science, and everyday life to solve problems involving ratios and amounts.
How do you set up a proportion?
To set up a proportion, you need to compare two ratios that are equal to each other. This can be done by setting one ratio equal to another, forming a mathematical statement in the form of a fraction. You can then cross multiply to solve for the missing value in the proportion.
What are the steps to solve a proportion?
To solve a proportion, first, cross multiply by multiplying the numerator of the first ratio by the denominator of the second ratio and vice versa. Then, set the two cross products equal to each other to form an equation. Finally, solve for the missing variable by dividing both sides by the coefficient of the variable.
How do you cross-multiply to solve a proportion?
To solve a proportion using cross-multiplication, you multiply the numerator of the first ratio by the denominator of the second ratio and set it equal to the product of the denominator of the first ratio and the numerator of the second ratio. This allows you to find the missing value in the proportion equation and solve for the unknown variable.
Can you solve a proportion by using fraction bars or models?
Yes, you can solve a proportion by using fraction bars or models. You can visually represent the given quantities as fractions and manipulate the bars or models to find equivalent ratios, thus solving the proportion. This visual representation can help make solving proportions more concrete and easier to understand, especially for those who are visual learners.
What is the difference between direct and inverse proportions?
In direct proportion, two quantities increase or decrease together at a constant ratio, meaning as one quantity increases, the other also increases and vice versa. In inverse proportion, as one quantity increases, the other decreases at a constant ratio, and vice versa. So, in direct proportion, both quantities move in the same direction, while in inverse proportion, they move in opposite directions.
How can you check if a solution to a proportion is correct?
To check if a solution to a proportion is correct, you can cross multiply. This means multiplying the outer numbers of the two fractions and then the inner numbers, and if the two products are equal, then the solution is correct. If the cross multiplication does not result in the same number, then the proportion is not correct.
Can proportions be used to solve real-world problems?
Yes, proportions can be used to solve real-world problems in various fields such as finance, engineering, science, and business. They are commonly used to scale measurements, find unknown quantities, make comparisons, and perform necessary calculations in a wide range of practical situations. By setting up ratios and proportions, individuals can find solutions to issues involving percentages, distances, areas, volumes, and many other real-world scenarios.
How are proportions used in scale drawings or maps?
Proportions are essential in scale drawings or maps as they allow for accurate representation of objects or areas in a smaller or enlarged format. By using ratios, scales can be determined to shrink or magnify measurements in a consistent and proportional manner. This ensures that distances, sizes, and dimensions are correctly depicted and can be accurately interpreted by users. Properly scaled maps or drawings maintain the relative proportions between various elements, enabling viewers to understand spatial relationships and make informed decisions based on the information presented.
Can you simplify or reduce a proportion to its simplest form?
Yes, to simplify a proportion to its simplest form, you need to divide both the numerator and denominator by their greatest common factor (GCF). By finding and dividing by the GCF, you will have a proportion in its simplest form with the smallest possible whole numbers in the numerator and denominator.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.





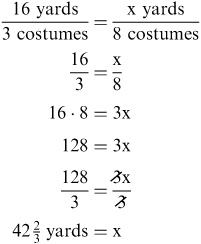




























Comments