Solving and Graphing Inequalities Worksheets

If you are a math teacher or a student in search of effective learning resources, you may want to consider using solving and graphing inequalities worksheets. These worksheets provide a thorough and structured approach to understanding and practicing the concepts of inequalities, making them suitable for both teachers and students looking to enhance their understanding of this mathematical entity and subject.

  Graphing Inequality Worksheets

---

  Algebra 1 Graphing Linear Equations Worksheet

---

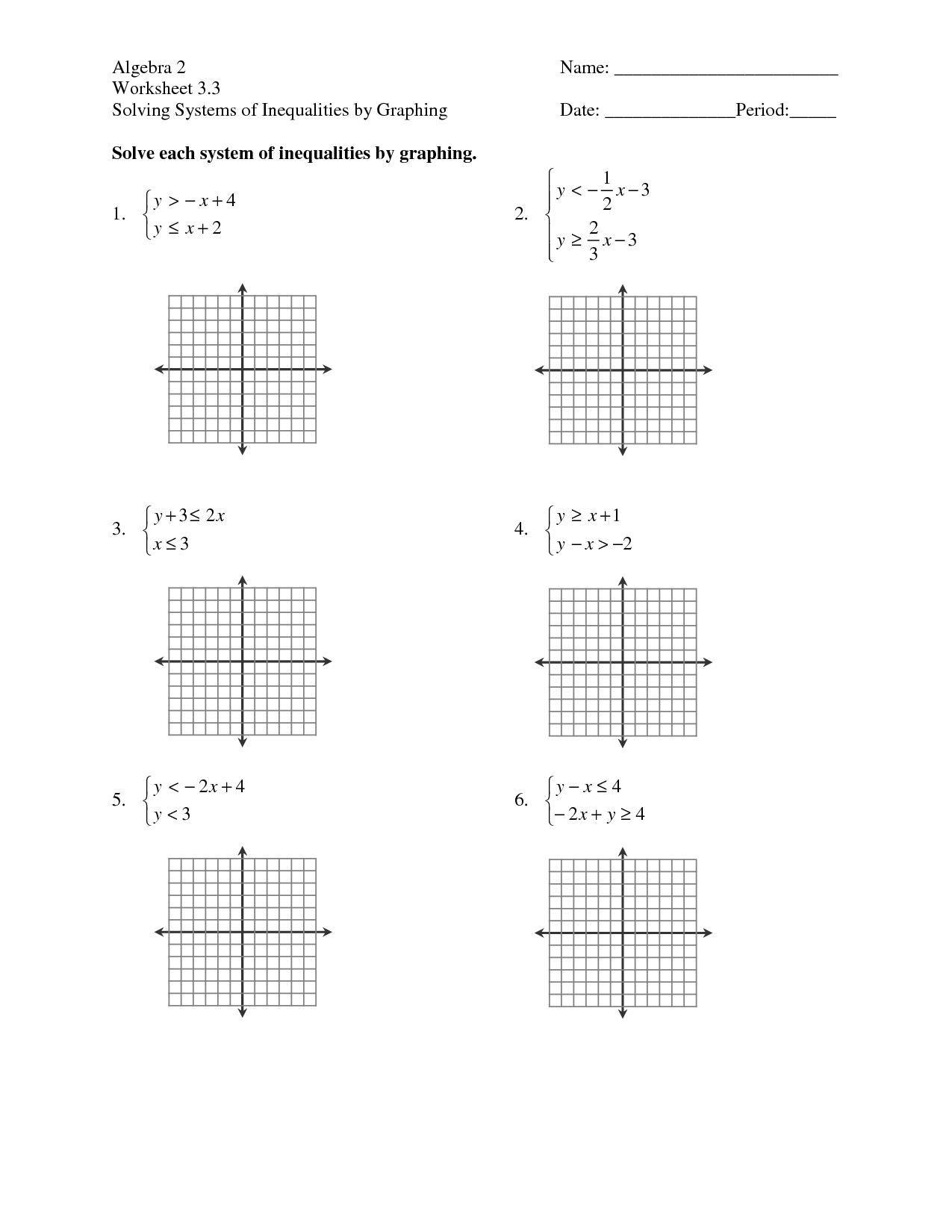
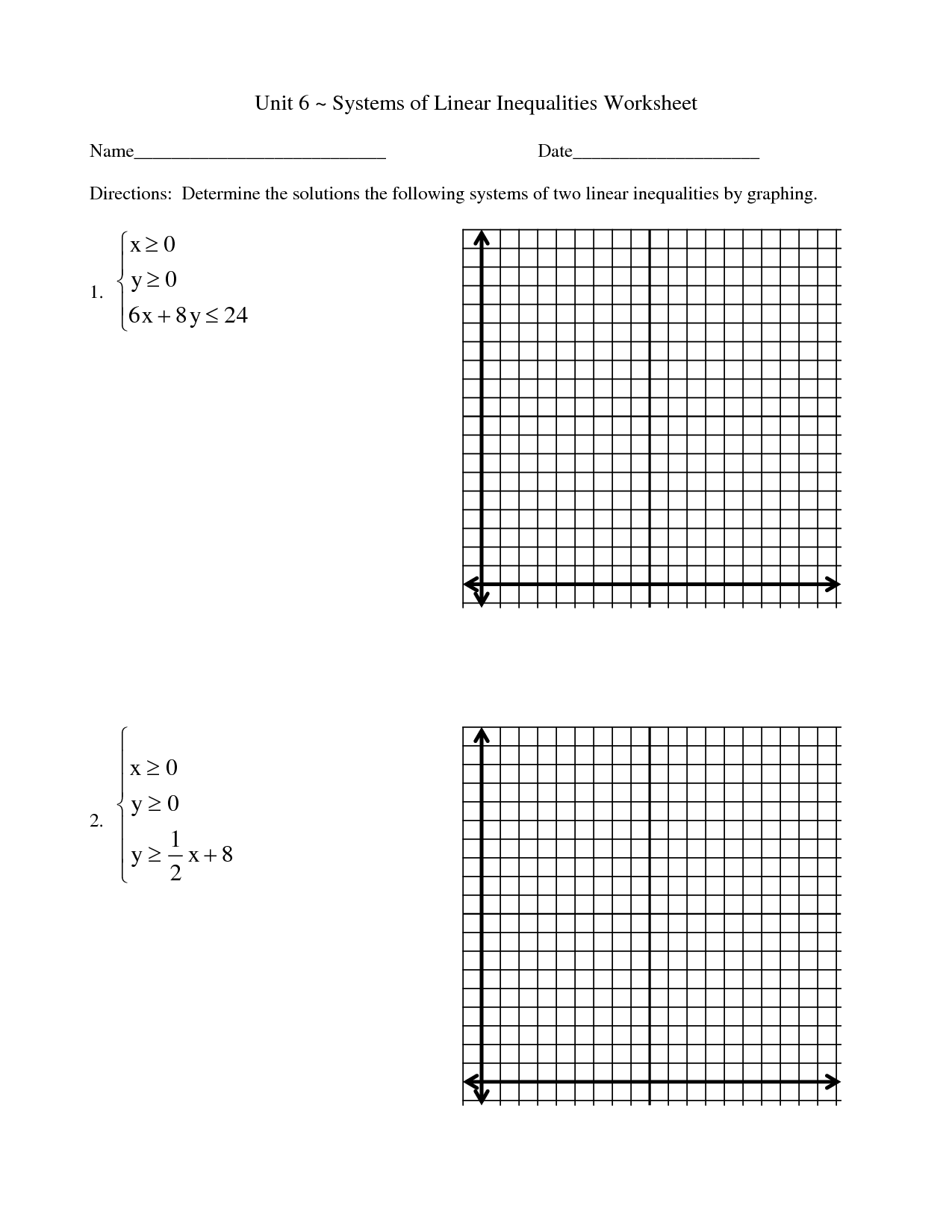
  Solving Systems of Inequalities by Graphing Worksheets

---

  Graphing Linear Inequalities Worksheet

---

  Algebra 1 Inequalities Worksheets Printable

---

  6th-Grade Inequalities Worksheets

---

  Two-Step Inequalities Worksheets

---

  Compound Inequalities Worksheets

---

  Absolute Value Inequalities Worksheets

---

  One Step Inequalities Worksheet

---

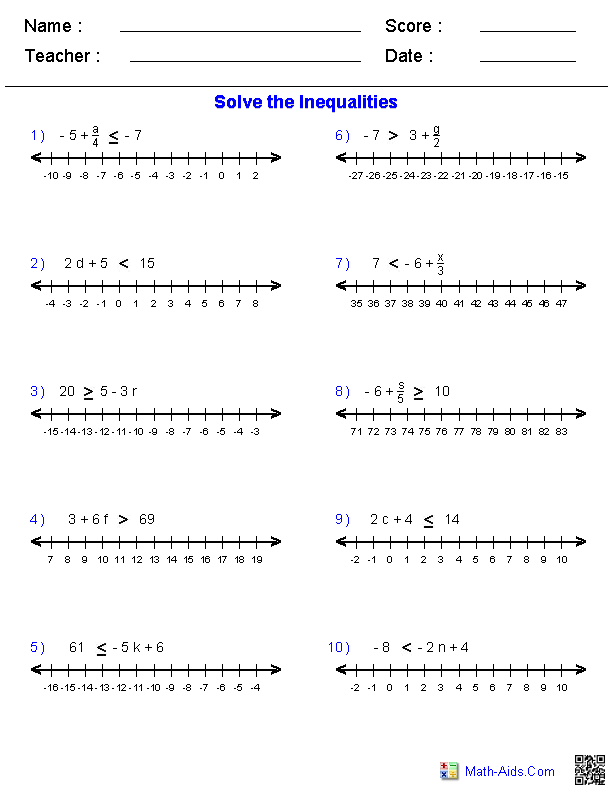
  Solving Inequalities Worksheets

---

  7th Grade Math Worksheets Algebra

---

  Solving Equations and Inequalities Worksheet

---

  Compound Inequality Worksheet

---

  Graphing Linear Inequalities Worksheet

---

  Graphing Quadratic Inequalities Worksheets

---

  Solving One Step Inequalities Worksheet

---

What is the purpose of solving and graphing inequalities worksheets?

The purpose of solving and graphing inequalities worksheets is to help students understand and practice the concepts of inequalities, including how to solve them algebraically and how to represent their solutions graphically on a number line. These worksheets help build problem-solving and critical thinking skills, as well as reinforce the concept of inequality and its application in real-life situations, such as in solving linear programming problems or representing constraints in a system of equations.

How do you determine the solution to an inequality equation?

To determine the solution to an inequality equation, you first isolate the variable on one side of the inequality sign. Then, you can solve for the variable just as you would in an equation. Remember to flip the inequality sign if you multiply or divide by a negative number. Finally, express the solution set in interval notation or using inequality notation, depending on the context of the problem.

What is the difference between an equality and an inequality?

An equality is a statement that shows that two quantities are the same, denoted by the equal sign (=), whereas an inequality is a statement that shows a comparison between two quantities, indicating that they are not necessarily the same, using symbols like < (less than), > (greater than), ? (less than or equal to), or ? (greater than or equal to).

How do you graph an inequality on a number line?

To graph an inequality on a number line, first identify the variable you need to plot. Next, determine if the inequality is inclusive (? or ?) or exclusive (< or >). If it is inclusive, represent the values with filled circles; if it is exclusive, represent them with hollow circles. Then, draw a line to the left or right of the circles, depending on whether the inequality is less than/greater than or less than or equal to/greater than or equal to. Finally, shade the region that includes all possible solutions to the inequality.

When graphing an inequality on a coordinate plane, what is the significance of shading?

Shading in graphing an inequality on a coordinate plane indicates the region of the plane that satisfies the inequality. The shaded area shows all the points that make the inequality true, helping to visually represent the solution set of the inequality.

How do you interpret the solution to a graphed inequality?

When interpreting the solution to a graphed inequality, you look at the shaded region on the graph. If the inequality is represented by a solid line, the shaded region indicates all the points that satisfy the inequality. If the inequality is represented by a dashed line, the shaded region indicates all the points that do not satisfy the inequality. The solution to the graphed inequality is the set of values that make the statement true based on where the shading falls on the graph.

What are the steps to solve a compound inequality?

To solve a compound inequality, first solve each individual inequality separately. Then, combine the solutions by considering the intersection or union of the intervals obtained. The conjunction "and" (represented by ?) is used for an intersection, while the disjunction "or" (represented by ?) is used for a union. Finally, express the final solution as an interval or a set of inequalities depending on the nature of the compound inequality. Remember to apply the same operations (addition, subtraction, multiplication, and division) to both sides of the inequalities to maintain their validity.

How do you graph a compound inequality on a number line?

To graph a compound inequality on a number line, first graph the two inequalities separately using open or closed circles to represent the endpoints and shading the region that satisfies each inequality. Then, identify the overlapping shaded regions to find where the solutions to both inequalities intersect, if any. Finally, shade the overlapping region to represent the solution set of the compound inequality on the number line.

What is the role of absolute value in solving and graphing inequalities?

The absolute value plays a crucial role in solving and graphing inequalities as it represents the distance of a number from zero on the number line. When solving absolute value inequalities, we consider both the positive and negative solutions, resulting in a range of possible values. Graphically, absolute value inequalities are represented by V-shaped graphs on the coordinate plane, where the solution involves the values within a certain distance from a specified point or range. By understanding the absolute value concept, we can effectively solve and graph inequalities with precision and accuracy.

How does solving and graphing inequalities relate to real-life situations?

Solving and graphing inequalities in real-life situations allows us to model and analyze various scenarios where we encounter constraints or limitations. For example, in budgeting, we can use inequalities to represent income, expenses, and savings goals. In manufacturing, we can use inequalities to optimize production processes within given resource constraints. By visualizing these inequalities on graphs, we can better understand the feasible solutions and make informed decisions in real-life situations.