Science Notation Worksheet

The Science Notation Worksheet is a helpful resource for middle school and high school students who are looking to master the fundamentals of scientific notation. This worksheet provides a clear and concise explanation of scientific notation and offers a variety of practice problems to reinforce the concept. Whether you are a student struggling to grasp this math topic or a parent looking for additional practice materials, the Science Notation Worksheet is designed to help improve understanding and confidence in using scientific notation.

  Scientific Notation Worksheets 8th Grade Answers

---

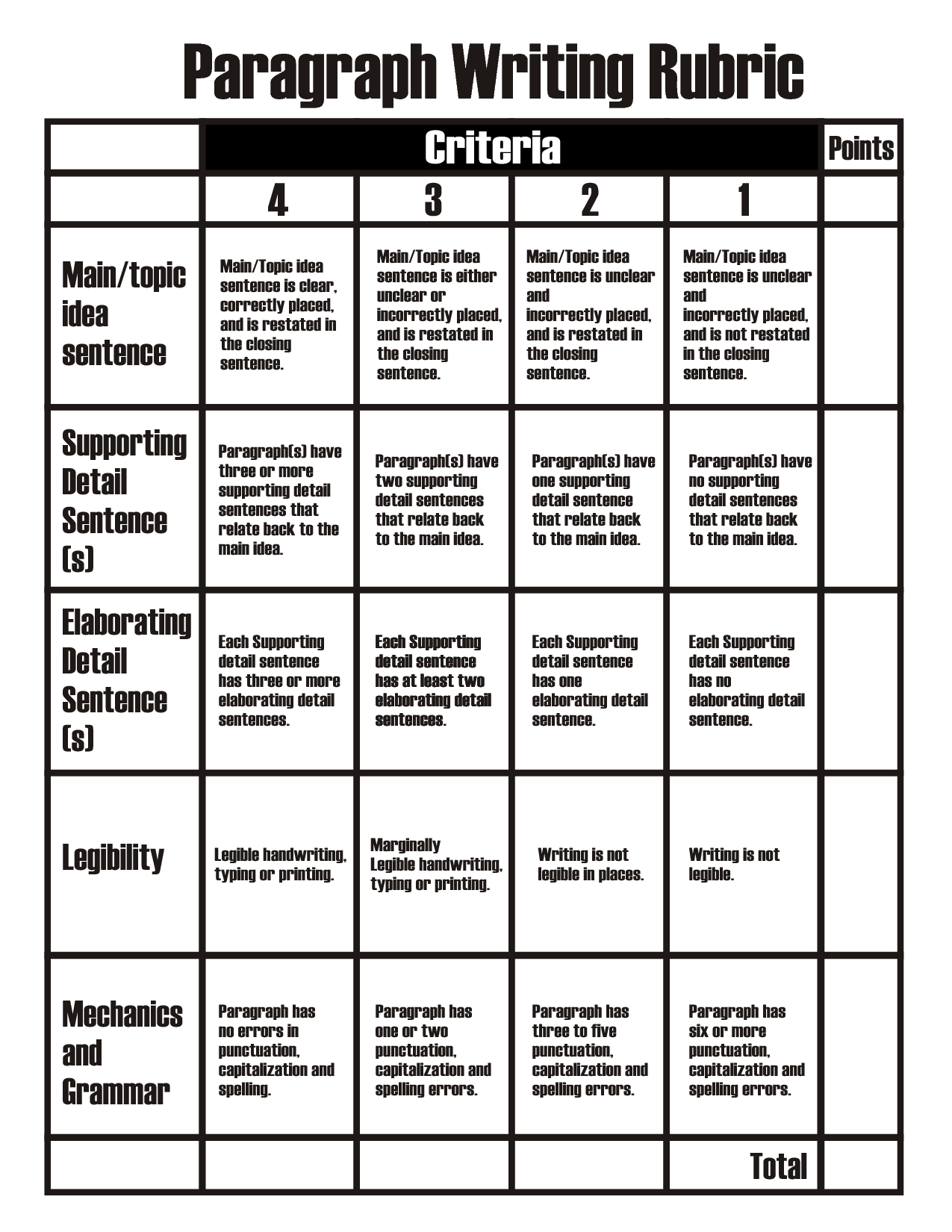
  Paragraph Writing Rubric

---

  Algebra 1 Function Notation Worksheet

---

  Chemistry Worksheet Answer Keys

---

  Exponential Notation Worksheets

---

  Electron Configuration Worksheet Answer Key

---

  Scientific Notation and Significant Figures Worksheet

---

  Binomial and Geometric Probability Worksheet

---

  Electron Configurations and Orbital Notation Worksheet

---

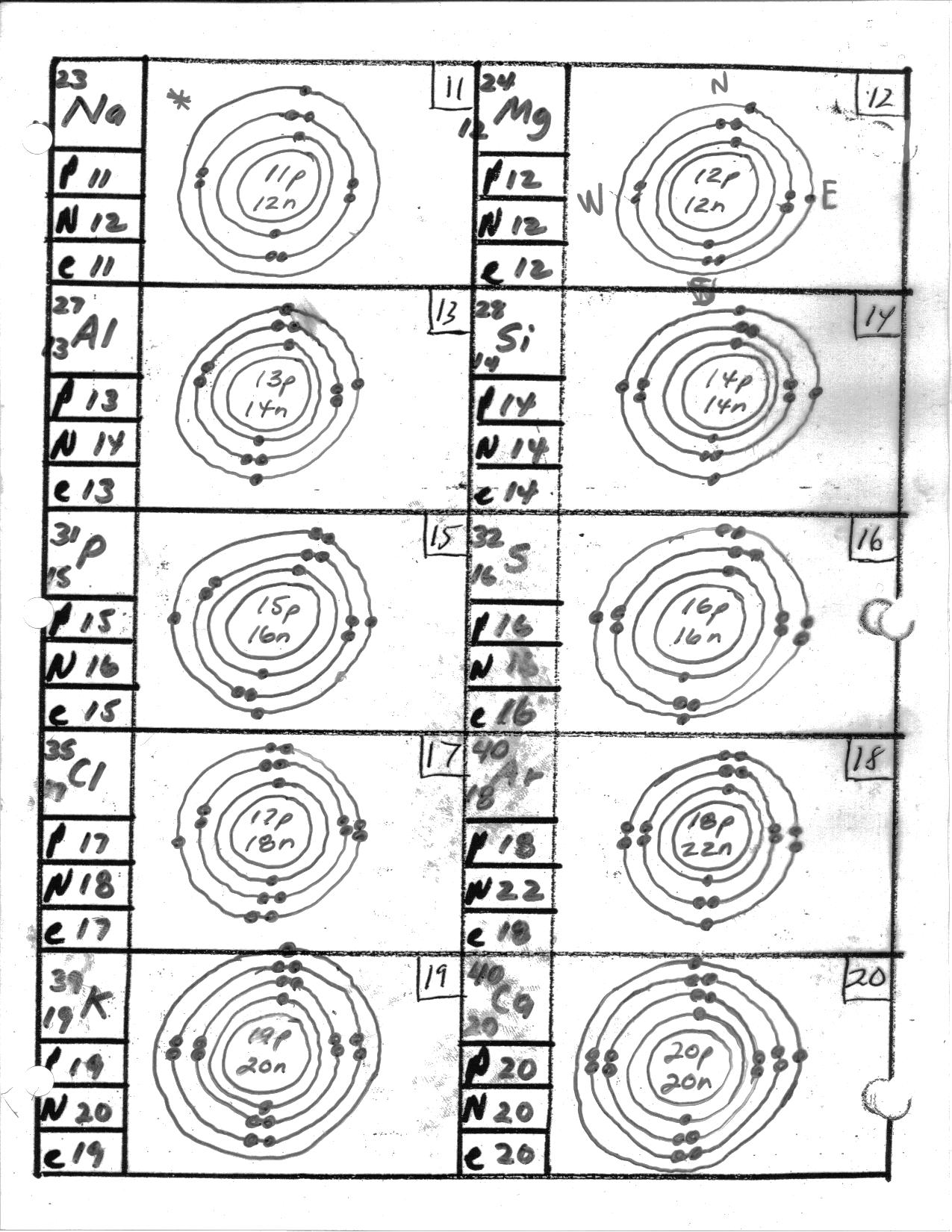
  Bohr Model Diagrams Worksheet Answers

---

  Dimensional Analysis Conversion Factors

---

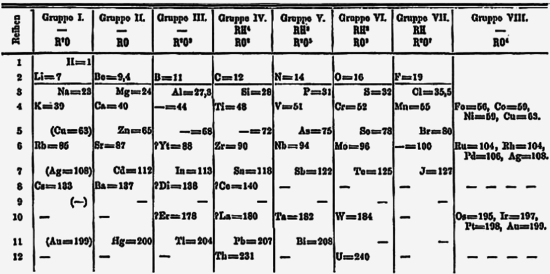
  Dmitri Mendeleev Periodic Table

---

What is scientific notation?

Scientific notation is a way to express very large or very small numbers in a compact and standardized form, by representing them as a single digit before the decimal point, multiplied by a power of 10. This notation is commonly used in scientific and mathematical calculations to easily work with numbers that have many digits.

How is scientific notation written?

Scientific notation is written by expressing a number as the product of a coefficient and a power of 10, where the coefficient is a number greater than or equal to 1 and less than 10, and the power of 10 indicates how many places the decimal point is moved. For example, the number 3,000,000 can be written in scientific notation as 3 x 10^6.

Why is scientific notation used?

Scientific notation is used to simplify writing and working with very large or very small numbers by expressing them in the form of a number multiplied by a power of 10. This allows for easier comparison and computation of numbers that have many digits, making calculations more manageable and efficient in fields like mathematics, science, and engineering.

How is a number written in scientific notation?

A number is written in scientific notation by expressing it as a coefficient multiplied by 10 raised to a certain power. The coefficient is a number between 1 and 10, and the power represents the number of times the decimal point was moved to create the coefficient. This notation is useful for representing very large or very small numbers in a concise way, making calculations and comparisons easier.

How do you convert a number from scientific notation to standard form?

To convert a number from scientific notation to standard form, you need to multiply the base number (the number before the "x10^" in scientific notation) by 10 raised to the power of the exponent (the number after the "x10^"). This will give you the equivalent number in standard form. For example, if you have 3.5 x 10^4 in scientific notation, you would multiply 3.5 by 10 raised to the power of 4 to get 35,000 in standard form.

How do you convert a number from standard form to scientific notation?

To convert a number from standard form to scientific notation, first move the decimal point to after the first non-zero digit, then count the number of places you moved the decimal. This number becomes the exponent of 10 in the scientific notation. Finally, write the number as a coefficient multiplied by 10 raised to the power of the exponent determined earlier.

What are the advantages of using scientific notation?

Scientific notation allows for expressing very large or very small numbers in a concise and standardized format, making calculations easier and faster. It also facilitates comparisons of numbers of different magnitudes and enables scientists and mathematicians to work with data involving very large or very small quantities more efficiently. Additionally, scientific notation helps reduce the likelihood of errors in calculations by minimizing the number of digits that need to be manipulated.

In scientific notation, what does the exponent represent?

The exponent in scientific notation represents the power of 10 by which the decimal part of the number is multiplied or divided to express the number in a more compact form. It determines the scale or magnitude of the number.

How can you determine the order of magnitude of a number in scientific notation?

To determine the order of magnitude of a number in scientific notation, you simply count the number of places the decimal point shifts to the left (or right) to get the number into a standard form where there is one non-zero digit to the left of the decimal point and the rest of the digits to the right of the decimal point. The number of places the decimal point shifts corresponds to the order of magnitude, with each shift representing a factor of 10.

How can scientific notation be used to compare and analyze large or small numbers easily?

Scientific notation can be used to compare and analyze large or small numbers easily by expressing them in a standardized form of a number multiplied by a power of 10. By converting numbers into this form, it allows for easier comparison of magnitudes and simplifies arithmetic operations. With scientific notation, large numbers are condensed into a more manageable format, while small numbers are represented more clearly without excessive zeros, making it efficient for scientific calculations and data analysis.