Rational Numbers 7th Grade Math Worksheets
Rational numbers are a fundamental concept in 7th grade math, and practicing with worksheets can greatly enhance understanding and proficiency in this subject. Whether you are a teacher searching for additional resources for your classroom or a parent wanting to provide extra practice for your child, these rational numbers worksheets are designed to cater to your needs.
Table of Images 👆
- Rational Numbers Worksheets
- Ordering Rational Numbers Worksheet
- Solving Equations with Rational Expressions Worksheet
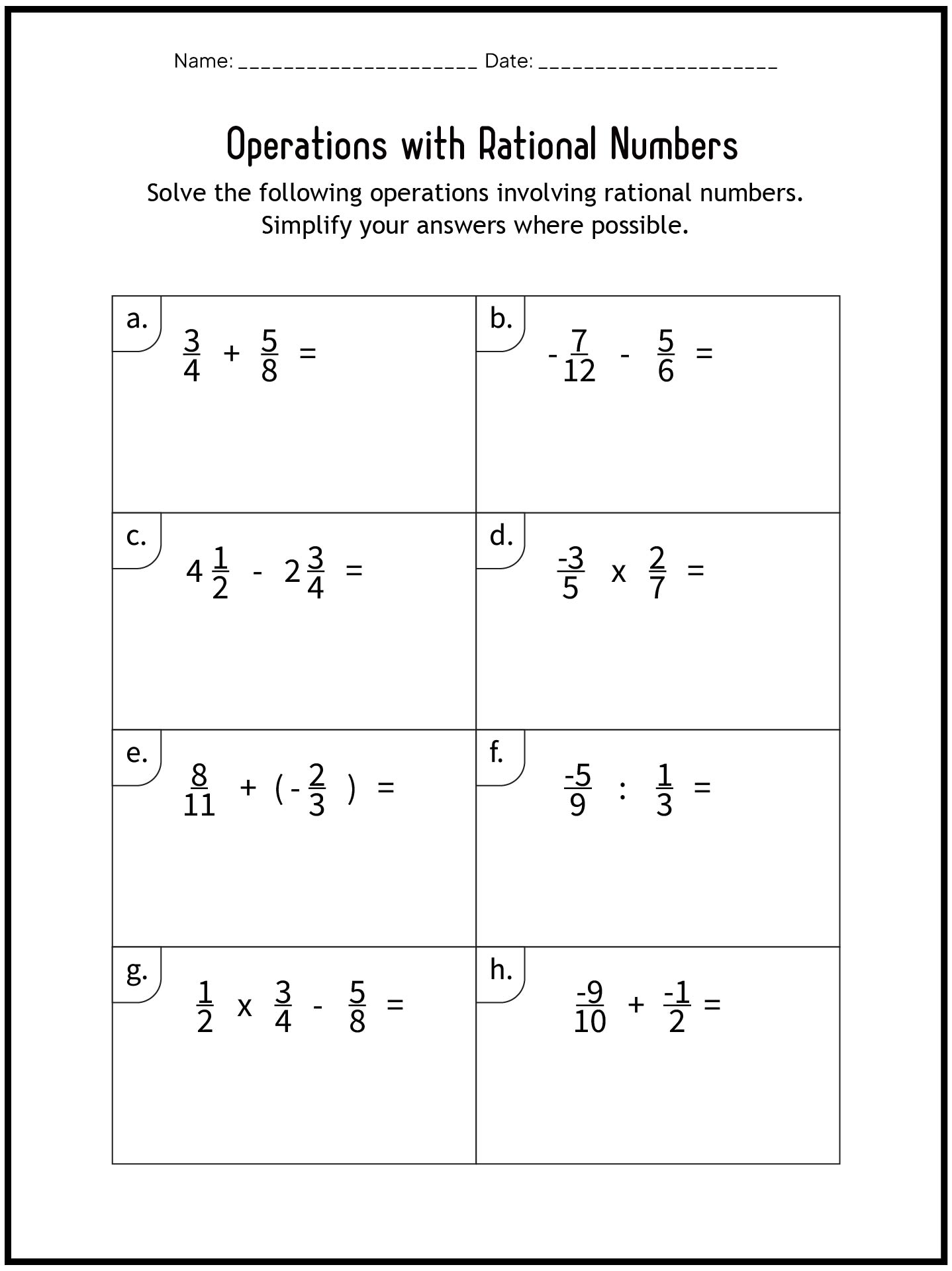
- 7th Grade Rational Numbers Practice Worksheets
- Rational Numbers 7th Grade Practice Sheets
- 7th Grade Comparing Rational Numbers Activities
- Fraction Decimal Conversion Worksheets for 7th Graders
- Advanced Rational Numbers Worksheets for 7th Graders
- 7th Grade Math Practice Sheets on Rational Numbers
- Rational Numbers Exercises for 7th Graders
- Comprehensive Rational Numbers Worksheets for Grade 7
- Grade 7 Rational Numbers Worksheets
- Math Worksheets for 7th Grade Rational Numbers

More Number Worksheets
Hundreds Chart Missing Numbers WorksheetTeen Number Practice Worksheet
Rational Numbers 7th Grade Math Worksheets
Number Cut Out Worksheet
Before and After Numbers Worksheets Grade 1
Missing Number Worksheets 1- 20
Kindergarten Number Worksheets 1 50
What is a rational number?
A rational number is a number that can be expressed as a fraction, where the numerator and denominator are integers and the denominator is not zero. This includes whole numbers, integers, and fractions. Rational numbers can be represented on a number line and can be precisely defined and calculated using arithmetic operations.
How are rational numbers different from irrational numbers?
Rational numbers can be expressed as a fraction of two integers, such as 3/4 or -5/2, while irrational numbers cannot be expressed as a simple fraction and have non-repeating and non-terminating decimal representations, like the square root of 2 or pi. Additionally, rational numbers can be written as terminating or repeating decimals, whereas irrational numbers cannot.
What are some examples of rational numbers?
Examples of rational numbers include integers (such as -3, 0, 5), fractions (such as 1/2, -3/4, 7/5), and terminating or repeating decimals (such as 0.6, -0.333, 2.25).
How can rational numbers be written as fractions?
Rational numbers can be written as fractions by expressing them as a ratio of two integers, where the denominator is not zero. For example, the rational number 0.5 can be written as the fraction 1/2, where the numerator is 1 and the denominator is 2. This is because 0.5 is equivalent to 1 divided by 2. Generally, any decimal number with a finite number of digits after the decimal point can be represented as a fraction by simplifying the ratio of the numerator and denominator.
Can rational numbers be negative?
Yes, rational numbers can be negative. Rational numbers include fractions such as -1/2, -3/4, or -5/6, where the numerator and denominator are integers and the denominator is not zero. This means that rational numbers can be positive, negative, or zero.
Are whole numbers and integers considered rational numbers?
Yes, both whole numbers and integers are considered rational numbers. Rational numbers are numbers that can be expressed as a ratio of two integers, where the denominator is not zero. Since whole numbers and integers can be expressed as a fraction with a denominator of 1, they fit the definition of a rational number.
Can rational numbers be expressed as terminating or repeating decimals?
Yes, rational numbers can be expressed as terminating or repeating decimals. A rational number is any number that can be written as a simple fraction where the denominator is not zero. When a rational number is expressed as a fraction, it can be written as a terminating decimal if the denominator is a power of 10 (e.g. 1/2 = 0.5), or as a repeating decimal if the fraction cannot be reduced to one with a denominator that is a power of 10 (e.g. 1/3 = 0.333...).
Can all fractions be considered rational numbers?
Yes, all fractions can be considered rational numbers. A rational number can be expressed as a ratio of two integers where the denominator is not zero. Since fractions are expressed as a ratio of two integers, they can always be represented as rational numbers.
Are square roots and cube roots rational numbers?
Square roots and cube roots can be rational numbers in some cases, but they are not always rational. A rational number is a number that can be expressed as a fraction of two integers. For example, the square root of 4 is a rational number (2), and the cube root of 8 is also rational (2). However, the square root of 2 and the cube root of 7 are both irrational numbers, meaning they cannot be expressed as a simple fraction.
How are rational numbers used in real-life situations?
Rational numbers are commonly used in real-life situations such as calculating distances, measuring ingredients in cooking, determining quantities in construction projects, managing finances, and predicting probabilities in statistics. They are essential for precise measurements, accurate calculations, and making informed decisions in various fields like engineering, science, finance, and everyday tasks.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.






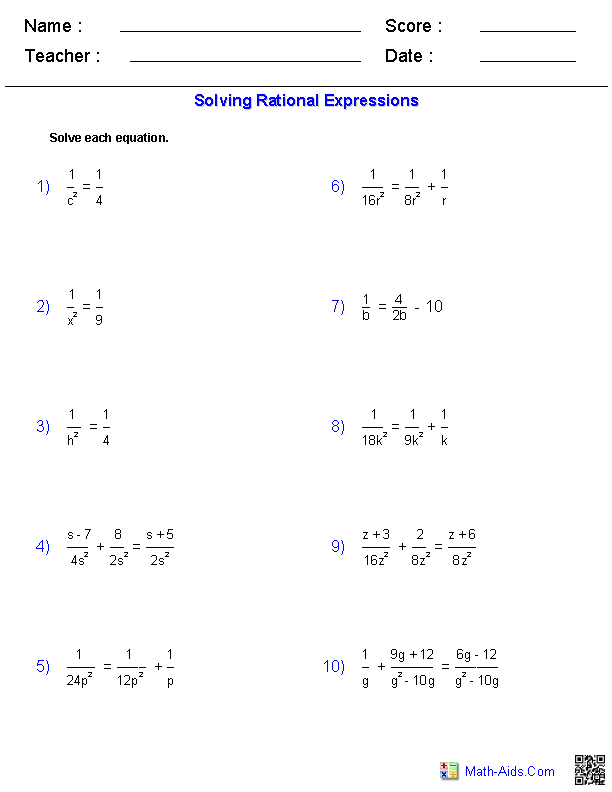





















Comments