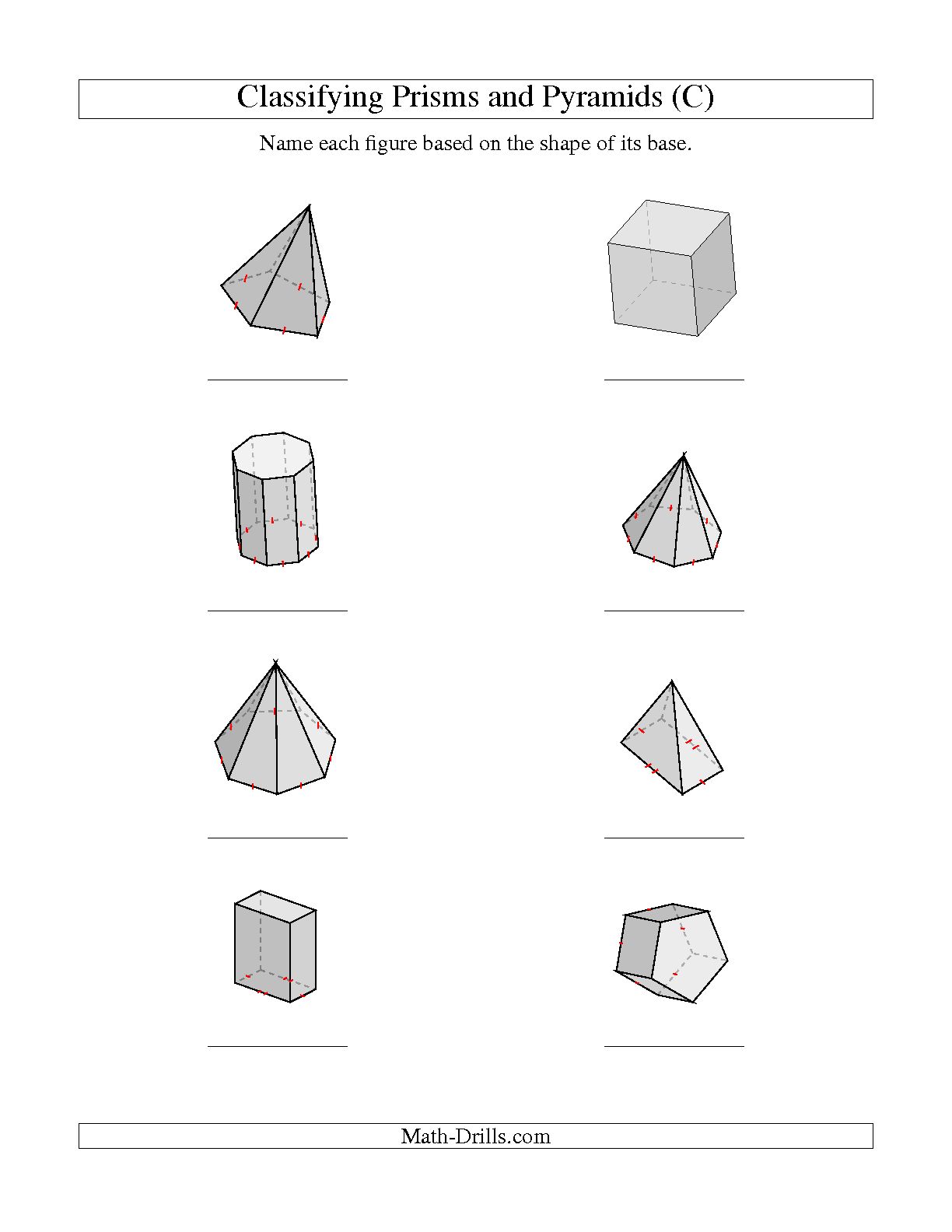
Prisms and Pyramids Worksheets

Prisms and pyramids are geometric shapes that play a crucial role in various areas of mathematics. Whether you are a student aiming to strengthen your understanding of these shapes or an educator searching for engaging resources to teach your students, worksheets can be a valuable tool. These structured activities provide an opportunity to practice and reinforce concepts related to prisms and pyramids, making learning enjoyable and effective.

  Classifying Prisms and Pyramids

---

  8th Grade Math Practice Worksheets

---

  7th Grade Math Worksheets

---

  3D modeling

---

  Volume Sphere Worksheet

---

  Pentagonal Prism Net Printable

---

  Measuring with Unifix Cubes Worksheet

---

  3D Shapes First Grade

---

What is a prism?

A prism is a geometric shape with flat surfaces that are typically in the form of a polygon at the base, with other faces connecting the corresponding sides of the base. It is a three-dimensional figure that has the same cross-section along its entire length, allowing light to be refracted and separated into its component colors when passing through it.

How many faces does a pyramid have?

A pyramid commonly has five faces: one base and four triangular faces that meet at a single point called the apex.

How is the surface area of a prism calculated?

The surface area of a prism can be calculated by adding together the areas of all the faces of the prism. The formula to find the surface area of a prism is 2(Abase) + (Ph), where Abase is the area of the base of the prism and Ph represents the lateral surface area, which is calculated by multiplying the perimeter of the base by the height of the prism.

Describe the difference between regular and irregular prisms.

Regular prisms have identical polygonal bases that are parallel and congruent, while irregular prisms have bases that are not congruent or parallel. Additionally, regular prisms have lateral faces that are rectangles, while irregular prisms have lateral faces that are not rectangles. Regular prisms have symmetry along the axis between their bases, whereas irregular prisms do not have this level of symmetry.

What is the formula for finding the volume of a pyramid?

The formula for finding the volume of a pyramid is V = 1/3 * base area * height, where V represents the volume of the pyramid, the base area is the area of the pyramid's base, and the height is the perpendicular distance between the base and the apex of the pyramid.

Explain how to determine the base area of a triangular prism.

To determine the base area of a triangular prism, you first need to find the area of the triangular base by multiplying the base length by the height of the triangle and dividing the result by 2 (base x height / 2). Once you have the area of the base triangle, you can then multiply it by the length of the prism (the distance between the two triangular bases) to get the total base area of the triangular prism.

What are some examples of everyday objects that are prisms?

Some examples of everyday objects that are prisms include a pencil sharpener, a rectangular tissue box, a book, a wallet, and a doorstop. These objects have a three-dimensional shape with two parallel and congruent polygonal faces, along with rectangular faces connecting the corresponding sides of the polygons.

How many vertices does a triangular pyramid have?

A triangular pyramid has 4 vertices.

Describe the relationship between the height and volume of a pyramid.

The volume of a pyramid is directly proportional to its height. This means that as the height of a pyramid increases, so does its volume. Similarly, if the height decreases, the volume of the pyramid will also decrease. This relationship is based on the formula for the volume of a pyramid, which includes the height as a factor in its calculation.

What are some mathematical properties of prisms and pyramids?

Some mathematical properties of prisms and pyramids include having bases that are polygons, lateral faces that are rectangles in prisms and triangles in pyramids, equal base and top faces in prisms, and a height perpendicular to the bases. Prisms have the same cross-section along the height, while pyramids have a single apex vertex and a base that is a polygon with the same number of sides as the apex. Both shapes have a volume calculated by multiplying the area of the base by the height.