Pre Calculus Worksheets

Pre Calculus Worksheets are a valuable resource for students looking to reinforce their understanding of key mathematical concepts. These worksheets provide a wide range of practice problems, allowing students to apply their knowledge and develop their problem-solving skills. Whether you are a high school student preparing for an exam or a college student aiming to excel in your pre calculus course, these worksheets offer a systematic approach to mastering the material.

  Arithmetic and Geometric Sequences Worksheets

---

  Algebra Joke Worksheets

---

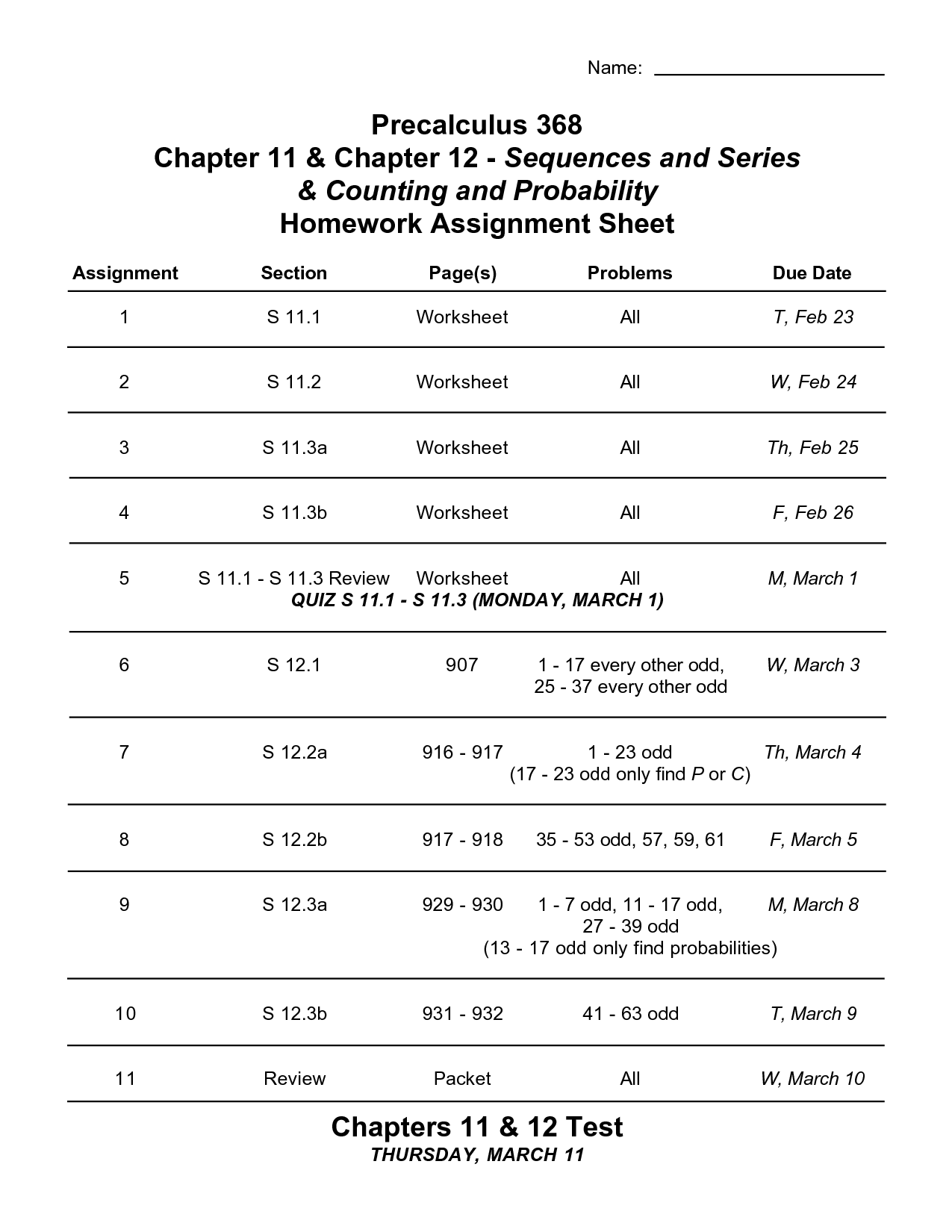
  Printable Precalculus Worksheets

---

  Business Math Worksheets for High School

---

  Simplifying Trig Expressions Worksheet

---

  Logarithm Worksheet Precalculus

---

  Geometry Chapter 1 Study Guide

---

  Exponential Functions Worksheet PDF

---

  Calculus Series and Sequences Cheat Sheet

---

  Honors Pre-Calculus Worksheets with Answer Sheet

---

  Precalculus Worksheets High School

---

  Precalculus Practice Worksheets with Answers

---

What are the basic concepts covered in precalculus worksheets?

Precalculus worksheets cover basic concepts such as functions, trigonometry, algebraic expressions, equations, inequalities, polynomials, rational functions, exponential and logarithmic functions, vectors, matrices, and sequences and series. These worksheets are designed to help students build a strong foundation in mathematical skills and prepare them for more advanced topics in calculus.

How do you solve a system of equations using matrices in precalculus?

To solve a system of equations using matrices in precalculus, you first need to write the system of equations in matrix form, with the coefficients of the variables and the constant terms organized in a matrix. Then, you create an augmented matrix by joining the coefficient matrix with the constant matrix. Next, use row operations to reduce the augmented matrix to row-echelon form or reduced row-echelon form. From this form, you can easily solve for the variables by back-substitution or other methods. Finally, interpret the results to find the values of the variables that satisfy all the equations in the system.

What is the difference between a function and an equation in precalculus?

In precalculus, a function is a relation between two sets where each element in the first set (called the domain) corresponds to exactly one element in the second set (called the range). Functions are typically denoted using functional notation, like f(x), and can be represented in various forms, such as algebraic expressions, tables, graphs, or verbal descriptions. On the other hand, an equation is a statement that two expressions are equal, often involving variables. Equations can be used to represent relationships between quantities and can involve operations like addition, subtraction, multiplication, division, exponents, and roots. While functions describe a specific relationship between inputs and outputs, equations are mathematical sentences that may or may not involve functions.

How do you find the domain and range of a given function?

To find the domain of a given function, you need to identify all possible input values that the function can accept without causing an error, such as dividing by zero or taking the square root of a negative number. The range of a function represents all possible output values that the function can produce based on the input values in its domain. To determine the range, you would evaluate the function for all values in its domain and identify the corresponding output values.

What are the steps for graphing a polynomial function on a coordinate plane?

To graph a polynomial function on a coordinate plane, first set up your axes with proper scales, marking the x and y-axis accordingly. Then, identify key points such as x-intercepts (where the graph crosses the x-axis), y-intercepts (where the graph crosses the y-axis), and any additional critical points. Next, plot these points on the graph. You can also find the leading coefficient to determine the end behavior of the function. Finally, connect these points smoothly to form the curve of the polynomial function on the graph.

How do you determine if a given function is odd or even?

To determine if a function is odd or even, you can use the properties of odd and even functions. A function is considered even if f(-x) = f(x) for all x in the domain, which means it is symmetric around the y-axis. On the other hand, a function is considered odd if f(-x) = -f(x) for all x in the domain, which means it is symmetric with respect to the origin. By evaluating the function at -x and comparing it to f(x), you can determine if it is odd, even, or neither.

What are the different types of conic sections and how are they represented algebraically?

The different types of conic sections are the circle, ellipse, parabola, and hyperbola. These curves can be represented algebraically through equations in the form Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0, where A, B, C, D, E, and F are constants characteristic of each type of conic section. For example, for a circle, the equation is x^2 + y^2 = r^2, for an ellipse, it is (x/a)^2 + (y/b)^2 = 1, for a parabola, it is y = ax^2 + bx + c, and for a hyperbola, it is (x/a)^2 - (y/b)^2 = 1 or (y/a)^2 - (x/b)^2 = 1.

How do you solve complex number equations in precalculus?

To solve complex number equations in precalculus, you can follow these steps: first, simplify the equation by performing any arithmetic operations on the complex numbers. Then, use properties of complex numbers, such as the conjugate or the polar form, to manipulate the equation and isolate the variable you are solving for. Finally, solve for the variable by either equating real parts or imaginary parts of the complex numbers. Remember to keep track of the components (real and imaginary parts) of the complex numbers throughout the process to arrive at the correct solution.

What are the properties and applications of logarithmic functions?

Logarithmic functions, often written as y = log(x), have the properties of being the inverse of exponential functions, meaning they can be used to solve equations involving exponential growth and decay. They are useful in representing data that spans several orders of magnitude, such as in finance, earthquakes, and sound intensity. Logarithmic functions are also utilized in various scientific fields, such as physics, biology, and chemistry, to simplify complex relationships and analyses. Additionally, they play a role in computer science and engineering for tasks like data compression and signal processing.

How do you perform operations with vectors in precalculus?

In precalculus, you perform operations with vectors by adding them component-wise, subtracting them component-wise, multiplying a vector by a scalar, determining the magnitude and direction of vectors, and finding the dot product and cross product of vectors. These operations involve manipulating the components of vectors based on specific rules and properties to calculate the result accurately.