Piecewise Functions Worksheet

Are you a math student in need of practice solving piecewise functions? Look no further, as we have a comprehensive and informative worksheet designed specifically for you. This worksheet will help you strengthen your understanding of piecewise functions by providing a variety of problems that focus on identifying the entity and subject of each function.

  Graph Piecewise Function Worksheet

---

  Piecewise Function Worksheet PDF

---

  Graphing Piecewise Functions Worksheet Answer

---

  Operations with Functions Worksheet

---

  Piecewise Functions Word Problems Worksheet

---

  Transformations of Functions Graphs Worksheet

---

  Greatest Integer Function Graph

---

  Linear Piecewise Functions Worksheet

---

  Transformation Worksheets Geometry Rules

---

  Skills and Applications Chapter 2 Answers

---

What is a piecewise function?

A piecewise function is a function that is defined by different rules or formulas for different intervals of its input. Each piece of the function is defined by a specific domain or range of values, and the function "switches" between these pieces depending on the input value. This allows for more complex and varied behavior than a single formula could provide.

How are piecewise functions defined?

A piecewise function is defined by different rules or functions that apply to distinct intervals within its domain. Each interval has its own function or expression that describes the behavior of the function within that specific range of input values. The function will have different expressions based on the intervals defined by specific conditions or boundaries.

What are the conditions or intervals in a piecewise function?

In a piecewise function, the conditions or intervals typically define when each portion of the function is applied. Each segment of the piecewise function is defined over a specific interval or set of conditions. These conditions or intervals outline when to use a particular function or formula within the piecewise function based on the input values or restrictions provided.

Can a piecewise function have multiple conditions or intervals?

Yes, a piecewise function can have multiple conditions or intervals. Each interval will have its own set of conditions and corresponding functions that are defined within that specific interval. This allows the piecewise function to behave differently in different parts of its domain based on the specified conditions.

How are the equations different for each interval in a piecewise function?

In a piecewise function, the equations differ for each interval based on the specified conditions or intervals. Each part of the piecewise function has its own distinct equation that is only valid within that specific interval or range of values. These equations are used to describe different behaviors or relationships for different parts of the overall function, allowing for a more complex and varied representation of the function across different intervals.

What does the graph of a piecewise function look like?

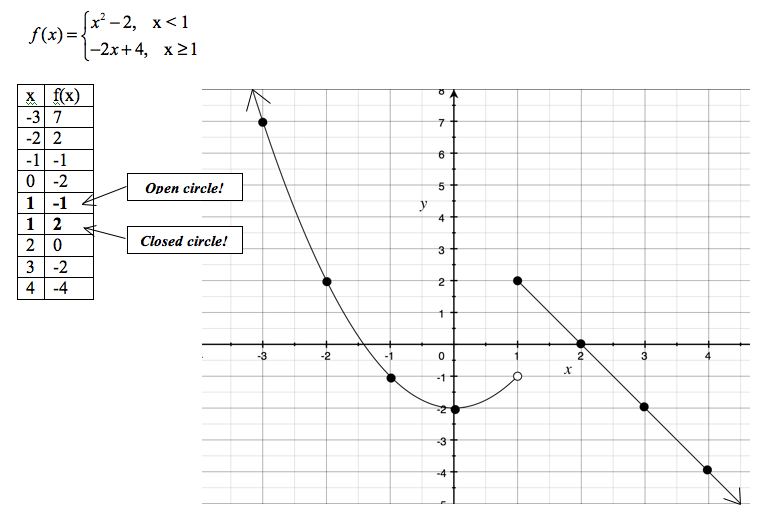
The graph of a piecewise function consists of multiple distinct segments or parts, each defined by a separate rule or formula on a specific interval. These segments may or may not be connected, resulting in discontinuities or gaps in the graph where the function changes behavior. Each segment follows the corresponding rule or formula defined for that interval, creating a piecewise continuous function.

How can you determine the domain and range of a piecewise function?

To determine the domain of a piecewise function, consider the domain of each piece separately and then combine them. The domain is the set of all valid input values that the function can accept. Likewise, to find the range, examine the output values of each piece of the function and combine them. The range is the set of all possible output values that the function can produce. Keep in mind any restrictions or conditions specified in each piece of the piecewise function when determining the domain and range.

In what situations are piecewise functions commonly used?

Piecewise functions are commonly used in mathematics to describe an equation that has different rules or formulas for different intervals of the independent variable. They are often used to model real-world phenomena that change behavior at specific points, such as a production cost that varies based on quantity, or a function that applies different rates for different levels of income. Additionally, piecewise functions are helpful in handling cases where a single formula is not sufficient to represent a complex relationship between variables.

How can you determine the value of a piecewise function for a specific input?

To determine the value of a piecewise function for a specific input, you need to identify which piece of the function corresponds to that specific input and then evaluate the corresponding expression or equation. Start by checking the condition for each piece of the function to find which one applies to the given input value. Once you identify the correct piece, substitute the input value into that specific expression or equation to calculate the output value.

How do you evaluate limits involving piecewise functions?

To evaluate limits involving piecewise functions, you first need to consider the different pieces of the function separately and evaluate the limit for each piece as it approaches the point of interest. Check if the limit exists for each piece and is continuous at the point. If the limits from both sides match at the point of interest, the overall limit exists at that point. If the limits are different from each side, the overall limit does not exist at that point. Be sure to carefully analyze the continuity and behavior of each piece to determine the limits involving piecewise functions.