Parabolic Line Worksheets

Parabolic line worksheets provide a practical and comprehensive way for students to practice and enhance their understanding of parabolic equations and graphing. Designed for middle school and high school students studying algebra and calculus, these worksheets offer a range of exercises and problems that focus on the entity of parabolic lines as well as the subject of graphing them accurately.

  Parabolic Curve Pattern Worksheets

---

  Parabolic Curve Worksheets

---

  Parabolic Curves Using Straight Lines Worksheet

---

  Parabolic Curve Worksheets

---

  Parabolic Line Designs

---

  Parabolic Line Worksheets Art

---

  Parabolic Reflector Template

---

  Parabolic Line Design Templates

---

  Parabolic Line Design Worksheets

---

  Cube Isometric Curve Stitching

---

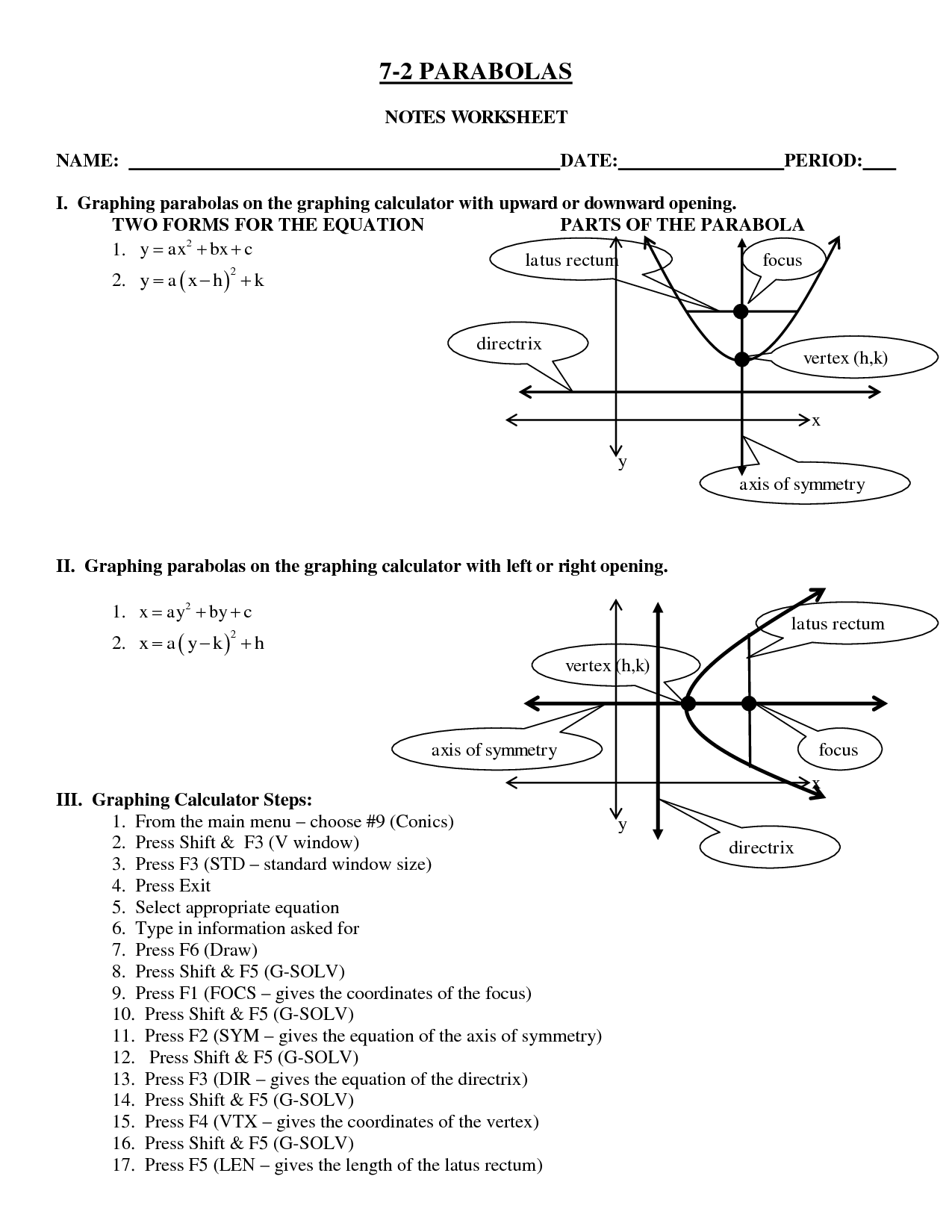
  Graphing Parabolas Worksheet

---

  Horizontal and Vertical Line Test

---

  Parabolic Curve

---

What is a parabolic line?

A parabolic line is a geometric shape formed by points that are equidistant from a fixed point (focus) and a fixed straight line (directrix). This shape resembles a U or a curve and is commonly seen in mathematics and physics, particularly in the study of parabolas.

How is a parabolic line different from a straight line?

A parabolic line is different from a straight line in that it is a curved line that follows the shape of a parabola, which is a U-shaped curve. In contrast, a straight line is a linear curve that extends indefinitely in both directions without any curvature. The slope of a parabolic line changes continuously, while the slope of a straight line remains constant.

What are some real-world examples of parabolic lines?

Some real-world examples of parabolic lines include the trajectory of a ball thrown into the air, the shape of satellite dishes, the design of automobile headlight reflectors, and the structure of suspension bridges. These examples demonstrate the practical application of parabolic lines in various fields such as physics, engineering, and architecture.

How can you determine the equation of a parabolic line?

To determine the equation of a parabolic line, you need to have the general form of a parabolic equation, which is y = ax^2 + bx + c. You can find the values of the coefficients a, b, and c by using the coordinates of any three points on the parabolic line. Plug in the x and y values of the points into the general form of the equation and solve the resulting system of equations to find the values of a, b, and c. Once you have these coefficients, you can write the equation of the parabolic line in the form y = ax^2 + bx + c.

What are the key features of a parabolic line?

A parabolic line is characterized by its symmetrical curve, with a single axis of symmetry known as the axis of the parabola. The vertex is the point where the axis intersects the curve, and the focus is a point through which all the parabola's rays reflect off of. The directrix is a line that is equidistant to all points on the parabola. The shape of a parabolic line is such that it extends infinitely in both directions, getting narrower or wider based on the coefficients of the quadratic equation that defines it.

How does the direction of the parabolic line affect its shape?

The direction of the parabolic line affects its orientation and curvature. A parabolic line that opens upwards has a U-shape, while one that opens downwards has an inverted U-shape. Changing the direction can also affect the location of the vertex and the direction in which the parabola opens towards the x or y-axis. Additionally, the steepness of the curve and how quickly it reaches its maximum or minimum point can vary depending on the direction of the parabolic line.

How do you graph a parabolic line?

To graph a parabolic line, start by plotting its vertex point, which is the highest or lowest point on the curve. Then, use the axis of symmetry to plot additional points on each side of the vertex at equal distances. Finally, connect the points smoothly to form the parabolic curve. Remember that the shape of the parabola can vary based on the coefficients of the quadratic equation being graphed.

What is the vertex of a parabolic line?

The vertex of a parabolic line is the point where the line changes direction, forming either a maximum point (for a parabola opening downwards) or a minimum point (for a parabola opening upwards). The vertex is often denoted as (h, k) in the vertex form of a parabolic equation, where "h" represents the x-coordinate and "k" represents the y-coordinate of the vertex.

How does changing the coefficients of a parabolic line equation affect its shape?

Changing the coefficients of a parabolic line equation affects its shape by stretching or compressing the parabola horizontally or vertically. Increasing the coefficient of the quadratic term enlarges the parabola vertically, while decreasing it makes the parabola narrower. Similarly, changing the coefficient of the linear term shifts the parabola left or right, and adjusting the constant term moves the parabola up or down. Overall, manipulating the coefficients alters the size, orientation, and position of the parabola while maintaining its basic curved shape.

How can you use parabolic line worksheets to practice solving problems related to parabolic lines?

You can use parabolic line worksheets to practice solving problems related to parabolic lines by working through different examples provided on the worksheet. This can help you understand the properties of parabolic lines, identify key components such as the vertex, focus, and directrix, and apply formulas to solve equations involving parabolic lines. By practicing with these worksheets, you can improve your problem-solving skills and familiarity with parabolic lines, ultimately enhancing your ability to solve similar problems independently.