Multiply Polynomials Box Method Worksheet
If you're searching for a comprehensive and straightforward way to practice multiplying polynomials, you've come to the right place. This blog post introduces an interactive and effective learning tool - the Multiply Polynomials Box Method Worksheet. Designed for students studying algebra, this worksheet focuses on multiplying polynomials using the box method, making it perfect for understanding the concept and developing essential problem-solving skills.
Table of Images 👆
- Multiplying Polynomials Box Method
- Multiplying Polynomials Box Method
- Factoring Box Method
- Multiplying Polynomials Box Method Worksheet
- Factoring Box Method
- Factoring Box Method Worksheet
- Multiplying Polynomials Using Box Method
- Area Model Multiplication Worksheets
- Multiplying and Factoring Polynomials Worksheet
- Partial Products Area Model Multiplication Worksheet
- Foil Math Worksheets
- Box Method Multiplication Polynomials
- Distributive Property Worksheets 7th Grade
- Homework Polynomials Worksheet
- Algebra Factoring Polynomials Worksheets with Answers
- Multiplying Polynomials Box Method
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is the purpose of the Multiply Polynomials Box Method Worksheet?
The purpose of the Multiply Polynomials Box Method Worksheet is to provide a structured and visual technique for multiplying polynomials. This method helps students organize the terms of the polynomials and systematically multiply them to find the correct product. It serves as a useful tool to understand and practice polynomial multiplication, leading to a better grasp of algebraic concepts.
How many polynomials are typically involved in each question?
In mathematics, it varies depending on the specific question or problem being addressed. Some questions may involve working with one polynomial, while others may involve multiple polynomials. It is not uncommon to encounter questions with one or two polynomials, but more complex problems may involve multiple polynomials and equations.
How are the polynomials represented in the box method?
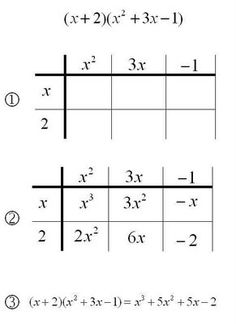
In the box method, each polynomial is represented by a rectangular box. The length and width of the box correspond to the terms of the polynomial, and the area of the box represents the product of the terms when multiplied together. By visually organizing the terms into boxes, the box method helps in understanding and simplifying polynomial multiplication and factoring.
What is the first step in using the box method to multiply polynomials?
The first step in using the box method to multiply polynomials is to draw a box or a grid. The box should have rows and columns that correspond to the number of terms in each polynomial being multiplied.
How does the box method help in organizing the multiplication process?
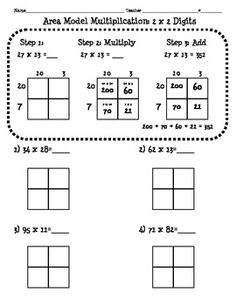
The box method helps in organizing the multiplication process by breaking it down into smaller steps within a structured visual framework. By creating boxes or grids, each representing a place value, the method helps to ensure that each digit is multiplied with the correct place value and the partial products are clearly written in their respective boxes. This systematic approach aids in reducing errors and confusion, allowing for a more organized and efficient multiplication process.
What is the significance of the rows and columns in the box method?
In the box method, the rows represent one factor being multiplied, while the columns represent the other factor being multiplied. The significance of organizing multiplication in this way is to visually break down the process and make it easier to multiply multi-digit numbers by showing how each part of one factor is being multiplied by each part of the other factor, helping in accurate calculation and better understanding of the multiplication process.
What information is placed in each box of the box method?
In the box method, each box is used to represent a digit or number in a mathematical operation. For example, in multiplication, each box contains a digit from one of the numbers being multiplied, and the result is calculated by multiplying the digits in each box according to their position and adding up the results. In division, each box may represent a digit in the dividend, divisor, or quotient, depending on how the method is being applied. Overall, the information placed in each box is a numerical value that contributes to the computation of the overall mathematical operation.
How do you determine the final answer using the box method?
To determine the final answer using the box method, you multiply the digits in each box of the grid, beginning from the rightmost box and moving left. Add up the results of each box multiplication (considering place value), starting from the rightmost column and carrying over when necessary, to get the final answer. Remember to consider place value, carry-over, and alignment in the process for accurate calculations.
Can the box method be used for multiplying any type of polynomials?
Yes, the box method can be used for multiplying any type of polynomials, including binomials, trinomials, and polynomials with more than three terms. The box method helps organize and visualize the multiplication process by breaking down the terms of each polynomial and multiplying them in a systematic way to find the product. It is an effective technique for simplifying the multiplication of polynomials regardless of their complexity.
What are the benefits of using the box method for multiplying polynomials?
The box method for multiplying polynomials is beneficial because it provides a visual representation of the terms being multiplied, making it easier to organize and keep track of each term. It helps break down the multiplication process into smaller steps, reducing the chances of errors. Additionally, the box method allows for a systematic approach to multiplying polynomials, making it especially helpful when dealing with more complex expressions.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.





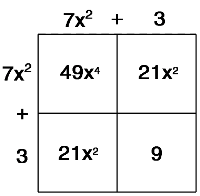
























Comments