Monomial Times Monomial Worksheet
Are you searching for a helpful resource to practice multiplying monomials? Look no further! This monomial times monomial worksheet is the perfect tool for individuals looking to strengthen their understanding of this concept. Designed to cater to students who are studying algebra or pre-algebra, this worksheet provides a comprehensive range of exercises that focus specifically on the entity of multiplying monomials. By using this worksheet, learners can expect to enhance their skills and confidently tackle future mathematical problems involving monomials.
Table of Images 👆
More Time Worksheets
Timed Multiplication Worksheets1 Minute Timed Addition Worksheets
Learning to Tell Time Worksheets Printables
Timed Addition Worksheets
Time in 15 Minute Increments Worksheet
What is a monomial?
A monomial is a mathematical expression that consists of only one term, which is typically made up of a constant (a numerical coefficient) and one or more variables raised to non-negative integer exponents.
What is the product of two monomials?
The product of two monomials is found by multiplying their coefficients and adding their exponents for each variable present. This results in a new monomial that represents the multiplication of the two original monomials.
How do you multiply monomials with the same variable?
To multiply monomials with the same variable, you simply multiply the coefficients and add the exponents of the variable. For example, if you have 3x^2 and 2x^3, you would multiply 3 and 2 to get 6 and add the exponents of x which gives you x^5.
How do you multiply monomials with different variables?
To multiply monomials with different variables, you multiply the coefficients together and then multiply the variables together by adding their exponents. For example, to multiply 3x^2 and 4y^3, you would multiply the coefficients (3 and 4) to get 12 and then multiply the variables (x^2 and y^3) to get x^2y^3. So, the result of multiplying 3x^2 and 4y^3 is 12x^2y^3.
Can you simplify the product of two monomials?
Yes, to simplify the product of two monomials, you can multiply the coefficients together and combine the variables by adding their exponents if they are the same.
Can you explain the concept of coefficient in a monomial?
In a monomial, the coefficient is the numerical factor that multiplies the variables. It represents the constant value present in the monomial. For example, in the monomial 5x^2, the coefficient is 5. The coefficient is essential in determining the overall value of the monomial when the variables are multiplied together.
What is the result when a monomial is multiplied by 1?
When a monomial is multiplied by 1, the result is the monomial itself. Multiplying any number or term by 1 will result in the same number or term, as any number multiplied by 1 is always equal to the original number.
Can you multiply a monomial by 0? If yes, what is the result?
Yes, you can multiply a monomial by 0. The result of multiplying any number or expression by 0 is always 0. So, if you multiply a monomial by 0, the product will be 0.
How do you raise a monomial to a power?
To raise a monomial to a power, you simply raise each term of the monomial to that power. This means multiplying each coefficient (the numerical part) by the power and adding the powers of the variables together. For example, if you have the monomial 3x^2 and you want to raise it to the power of 3, you would calculate (3^3)(x^2)^3 = 27x^6, by cubing both the coefficient and the exponent of x.
Can you provide an example of multiplying monomials with numerical coefficients?
Sure! An example of multiplying monomials with numerical coefficients would be: 2x * 3y = 6xy. In this case, we are multiplying the numerical coefficients (2 and 3) to get 6, and multiplying the variables (x and y) together to get xy.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.





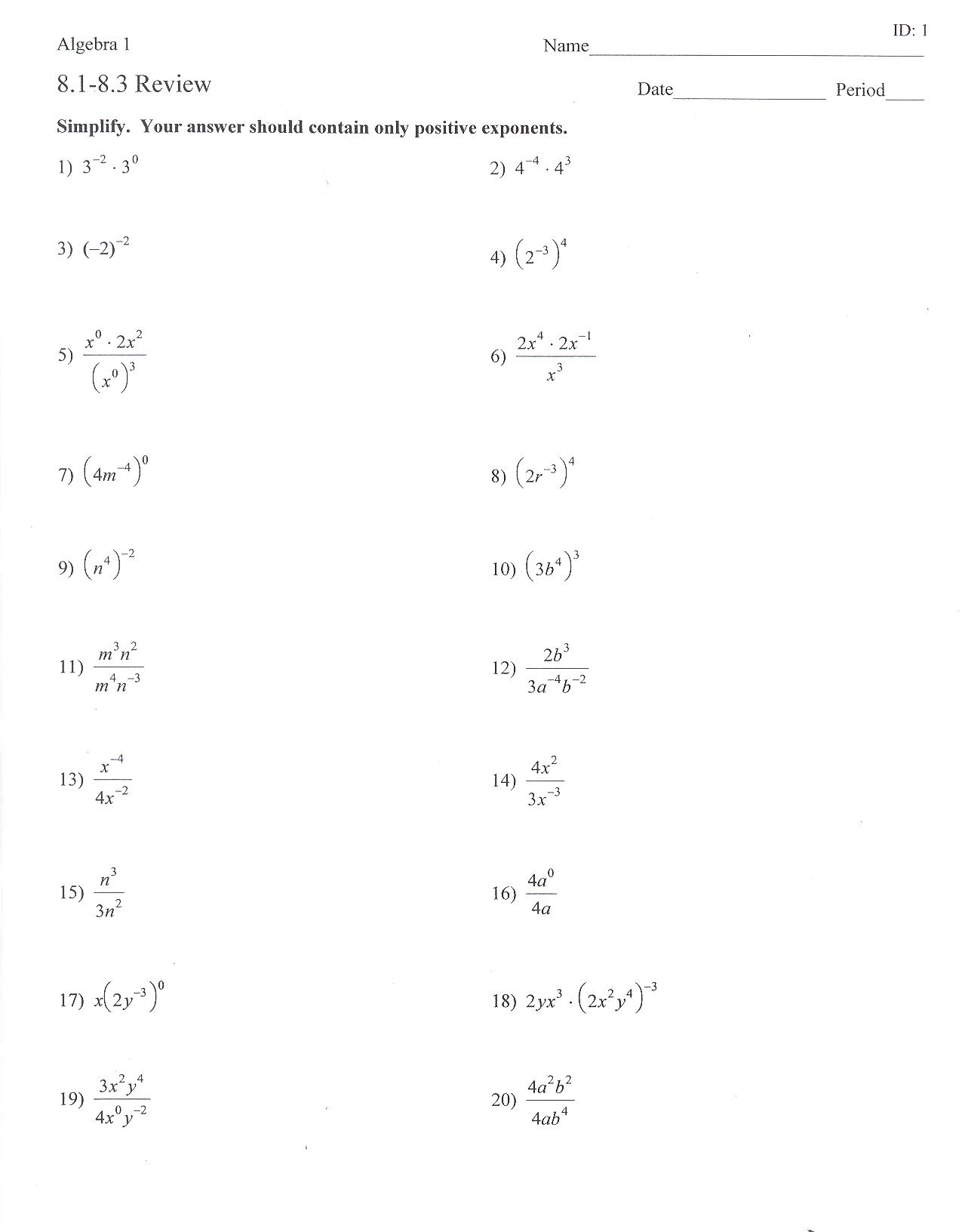


















Comments