Mixed Transformations Worksheets

If you're a teacher searching for worksheets that cover a variety of concepts related to mixed transformations, then you've come to the right place. These worksheets are designed to help students understand and practice transformations such as rotations, reflections, translations, and dilations. With clear instructions and engaging exercises, these worksheets provide a valuable resource for teaching and reinforcing these important geometric concepts.

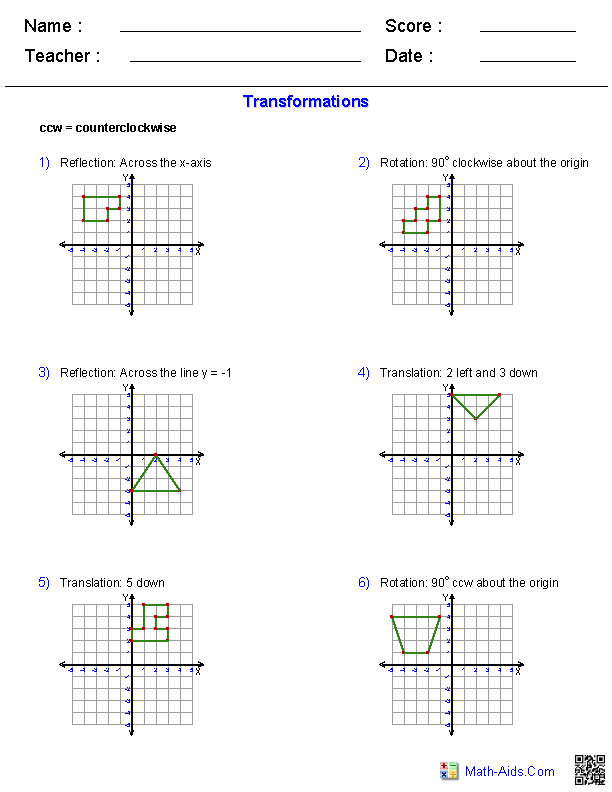
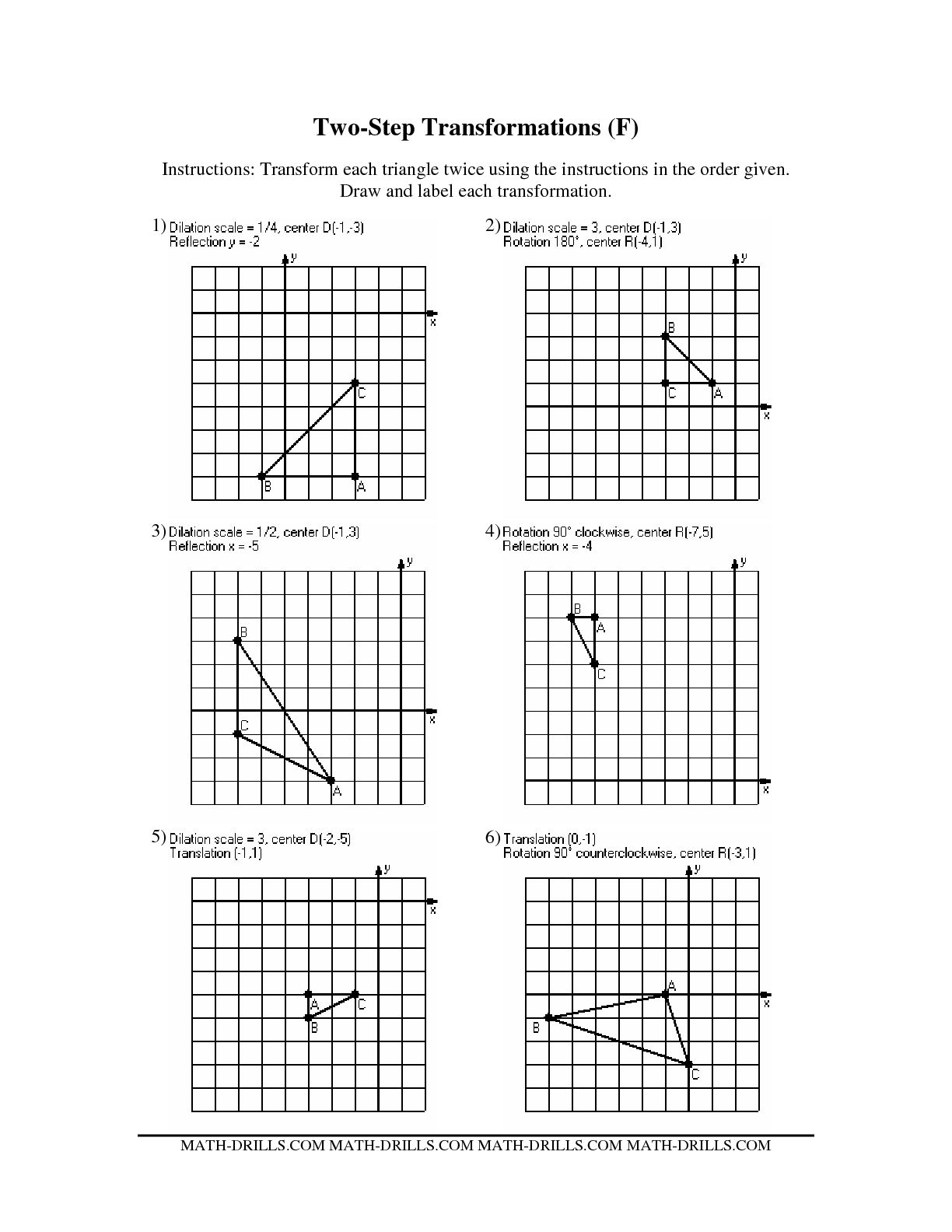
  Transformation Worksheets

---

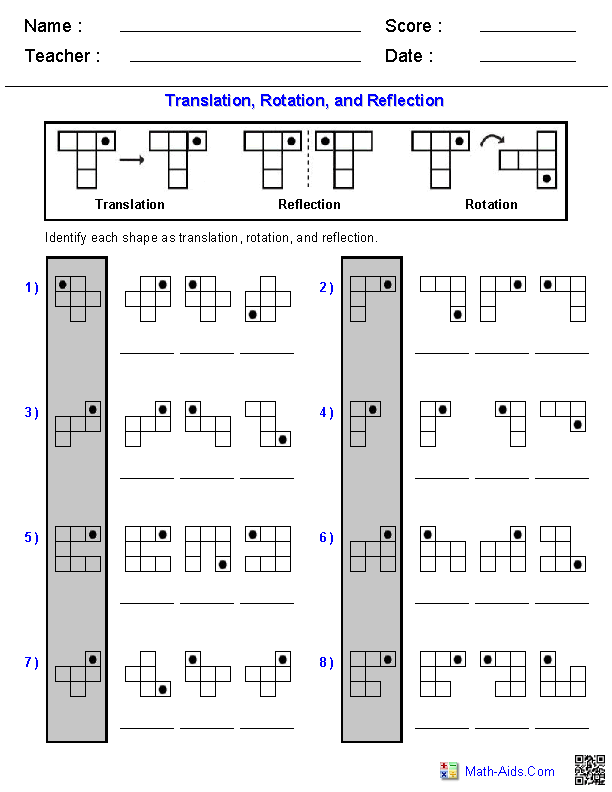
  Geometry Translation Reflection Rotation Worksheets

---

  Transformations Math Worksheets

---

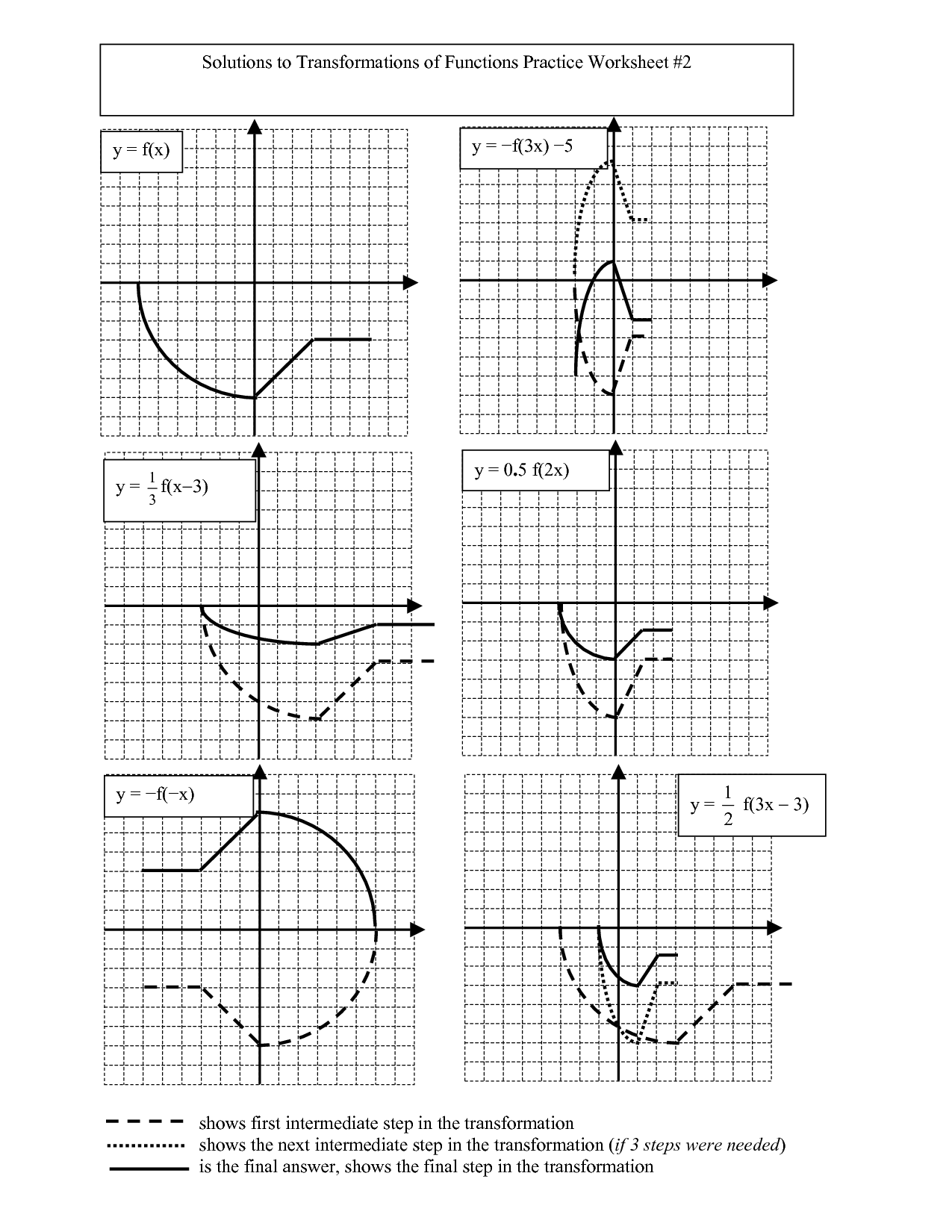
  Function Transformation Worksheet

---

  Sentence Transformation Worksheets

---

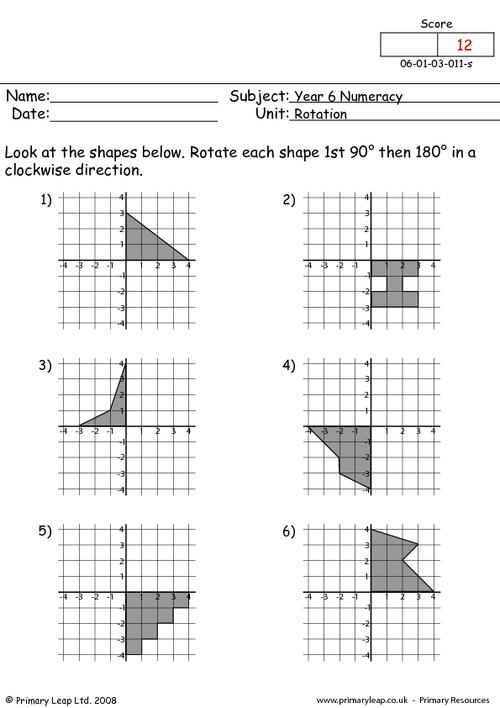
  Rotations Worksheets

---

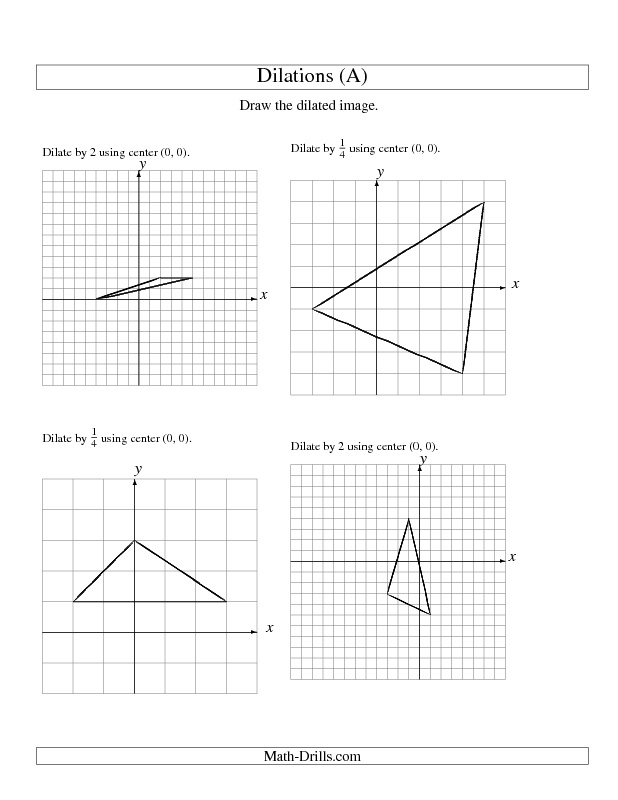
  8th Grade Math Dilations Worksheets

---

  Vocabulary Worksheet

---

  Renaming Mixed Numbers and Improper Fractions Pictures

---

  Parent Functions Algebra 2 Worksheets

---

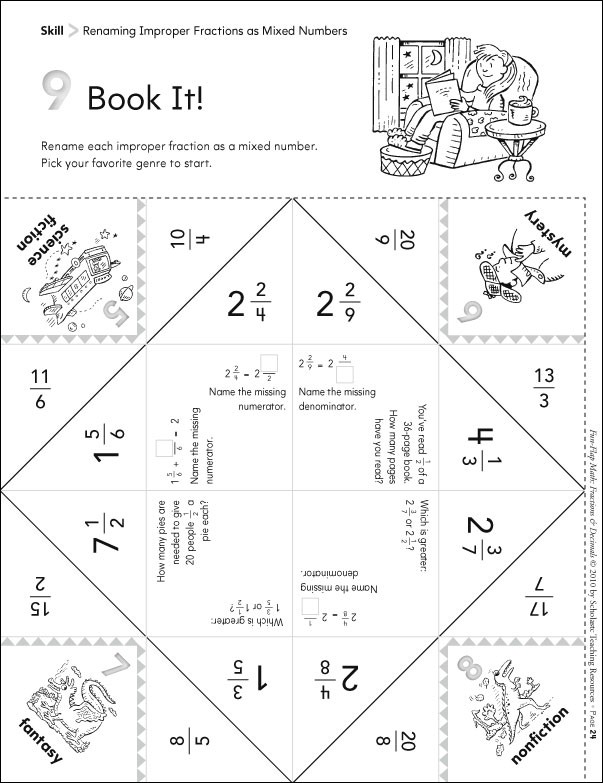
  Improper Fractions as Mixed Numbers Worksheet

---

What is a mixed transformation?

A mixed transformation is a combination of different types of transformations, such as translation, rotation, and scaling, applied to a geometric object. This allows for more complex changes in the position, orientation, and size of the object in a single transformation.

How can mixed transformations be represented mathematically?

Mixed transformations can be represented mathematically by combining different transformation matrices using matrix multiplication. Each individual transformation can be represented by a transformation matrix, where multiple transformations can be combined by multiplying the matrices in the order the transformations are applied. This allows for a concise mathematical representation of a series of mixed transformations in a single matrix form, facilitating efficient computation in computer graphics, robotics, and other fields where transformations are common.

What are the different types of transformations included in mixed transformations?

In mixed transformations, there are two main types of transformations: geometric transformations and non-geometric transformations. Geometric transformations involve changing the size, orientation, or position of an object, such as scaling, rotation, and translation. Non-geometric transformations, on the other hand, involve altering the appearance of an object without changing its shape, such as color adjustments, texture mapping, and filtering. These two types of transformations can be combined in various ways to create complex visual effects in computer graphics and image processing.

How can mixed transformations be applied to mathematical expressions or equations?

Mixed transformations can be applied to mathematical expressions or equations by combining different types of transformations such as translations, rotations, reflections, and dilations. These transformations can be used to manipulate and modify the original expression or equation in various ways, such as changing its position, orientation, or size. By applying a combination of these transformations, one can effectively alter the form of the mathematical expression or equation to suit specific needs or purposes.

What is the purpose of using mixed transformations in problem-solving?

The purpose of using mixed transformations in problem-solving is to allow for a flexible approach that can efficiently address a variety of complex situations. By combining different types of transformations such as translation, rotation, reflection, and dilation, mixed transformations offer a powerful way to manipulate and analyze shapes and patterns in geometry. This method helps in creating a comprehensive understanding of spatial relationships and transformations, enabling more effective problem-solving strategies in diverse mathematical contexts.

How can mixed transformations be used to simplify or manipulate equations?

Mixed transformations involve a combination of translation, reflection, rotation, and dilation. By using mixed transformations on equations, we can simplify or manipulate them by changing their position, orientation, or size, which can make them easier to work with or solve. For example, translating an equation can shift it to a new location on the coordinate plane, while reflecting it can change its orientation. These transformations can help us visualize patterns, identify symmetries, or solve equations more efficiently by altering their form in a strategic way.

In what scenarios can mixed transformations be used in real-life applications?

Mixed transformations can be used in real-life applications where a combination of different transformations is necessary to achieve a desired outcome. For example, in computer graphics, mixed transformations can be used to rotate, scale, and translate objects in a 3D space to create complex animations. In robotics, mixed transformations can be applied to manipulate robotic arms with multiple joints in various directions. In medical imaging, mixed transformations can be used to align and register different medical scans from different imaging modalities to improve diagnostic accuracy. Overall, mixed transformations are valuable in scenarios where a combination of different transformations is needed to perform complex operations or analyses.

Can mixed transformations be used to solve problems in geometry? If so, how?

Yes, mixed transformations can be used to solve problems in geometry by combining different types of transformations such as translations, rotations, reflections, and dilations. By applying a sequence of these transformations, geometric figures can be manipulated to determine properties like symmetry, congruence, and similarity. This approach allows for a deeper understanding of spatial relationships and can be used to solve a variety of geometrical problems efficiently.

What are some common mistakes or errors that can occur when applying mixed transformations?

Some common mistakes or errors that can occur when applying mixed transformations include incorrectly combining translation, rotation, and scaling operations in the wrong order, not considering the effects of pivot points or reference frames when applying transformations, and using non-uniform scaling which can lead to distorted or skewed objects. It is important to understand the order of operations for transformations and how they interact with each other to avoid these errors and ensure accurate results in computer graphics or animation.

How can students practice and improve their skills in using mixed transformations?

Students can practice and improve their skills in using mixed transformations by regularly completing exercises or problems that involve a combination of different types of transformations such as translation, rotation, reflection, and dilation. They can also use online resources and educational apps that provide interactive tools for practicing mixed transformations. Additionally, working on real-world applications or projects that require the use of mixed transformations can help reinforce their understanding and proficiency in this concept. Practice, consistency, and seeking help from teachers or peers when needed are key strategies for mastering mixed transformations.