Matrix Algebra Worksheets
Matrix algebra worksheets are an invaluable tool for students and professionals seeking to deepen their understanding of this important subject. Designed to provide comprehensive practice and reinforcement, these worksheets cater to both beginners and advanced learners who are eager to develop their skills in manipulating and solving problems involving matrices and their properties.
Table of Images 👆
- Printable Matrix Worksheets
- Math Matrix Worksheets
- Matrix Multiplication Worksheet Math
- Algebra 2 Matrices Worksheets
- Algebra 2 Matrices Worksheets
- Rules of Matrix Multiplication Worksheets
- Matrix Multiplication Worksheet
- Matrices Worksheets
- Matrix Algebra 2 Worksheet
- High School Math Worksheets Multiplication
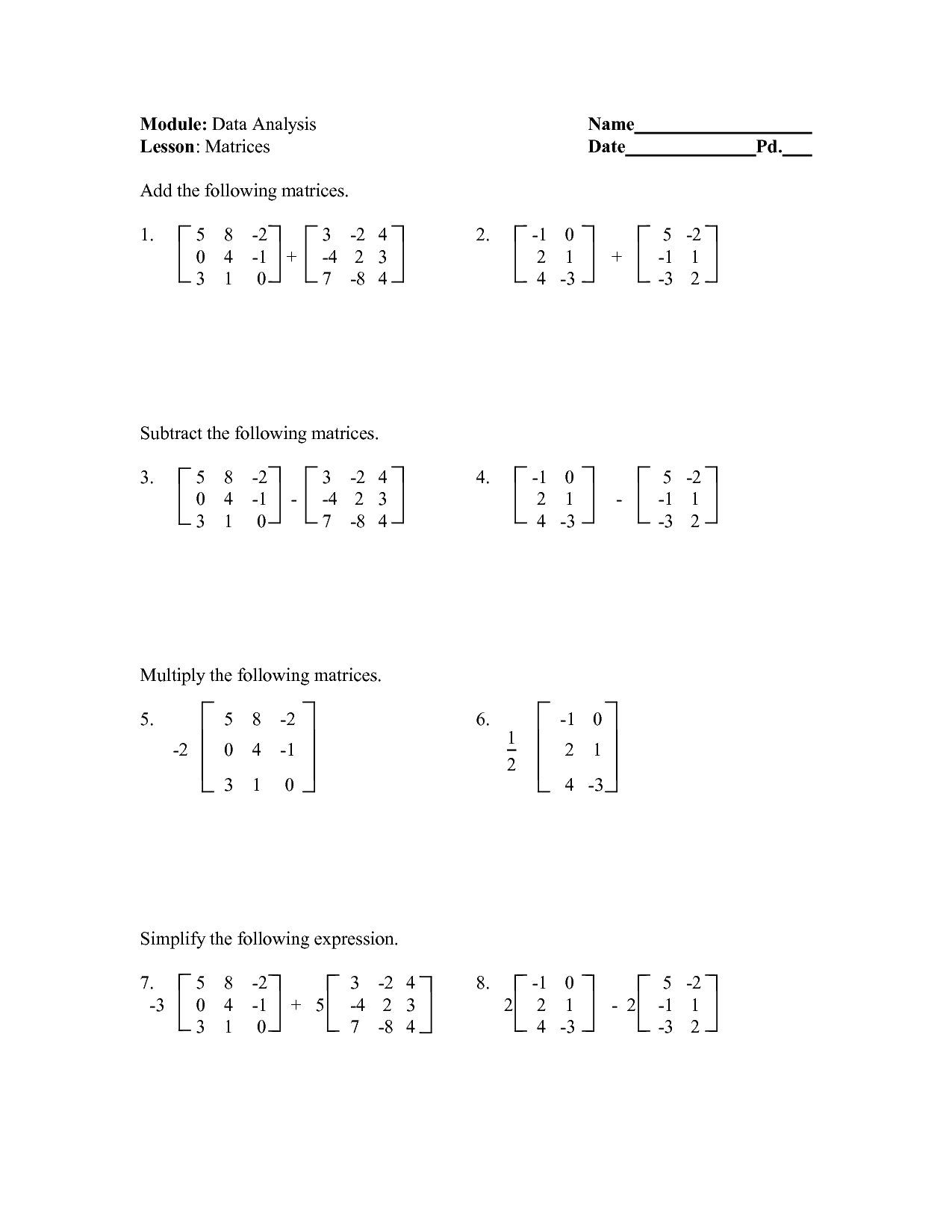
- Adding Matrices Worksheet
- Matrix Multiplication Worksheet Math
- Matrix Practice Worksheet
- Algebra 2 Matrices Worksheets
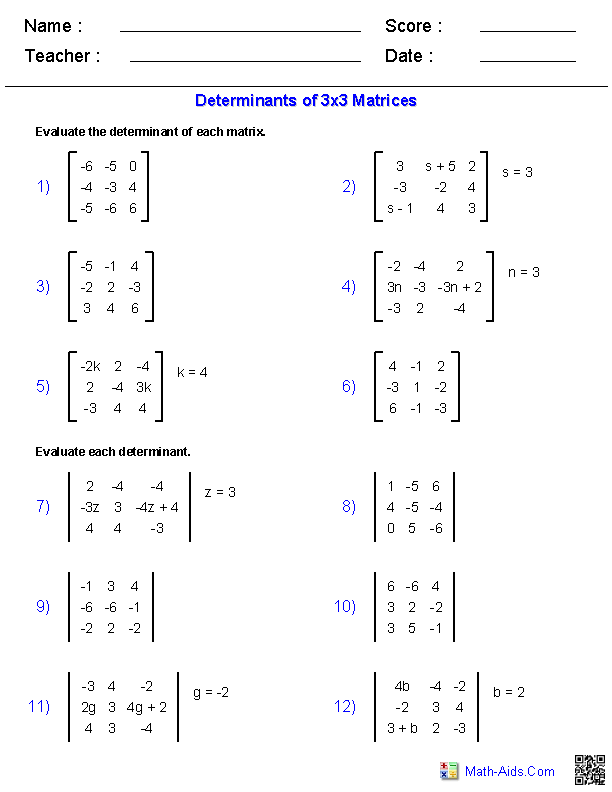
- Cramers Rule for 3X3 Matrix
- Inverse Matrices Worksheet
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is matrix algebra?
Matrix algebra is a branch of mathematics that deals with operations and properties of matrices, which are arrays of numbers arranged in rows and columns. In matrix algebra, various mathematical operations such as addition, subtraction, multiplication, and inversion are carried out with matrices to solve equations, analyze systems of equations, and perform transformations in fields such as physics, engineering, computer science, and economics.
What are the basic operations in matrix algebra?
The basic operations in matrix algebra include addition, subtraction, multiplication, and scalar multiplication. These operations follow specific rules and properties that allow for various manipulations and calculations with matrices.
How do you add two matrices?
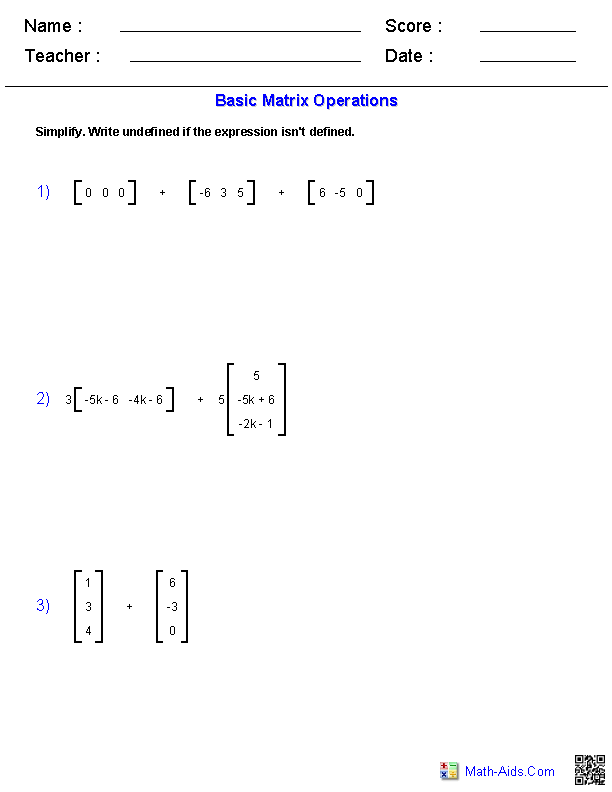
To add two matrices, you simply add the corresponding elements of the matrices together. For example, to add matrix A and matrix B, you add A[0][0] to B[0][0], A[0][1] to B[0][1], and so on, to get the resulting matrix. The matrices being added must have the same dimensions for this operation to be possible.
How do you subtract two matrices?
To subtract two matrices, simply subtract corresponding elements of the matrices. The matrices must have the same dimensions for subtraction to be possible. Subtract the elements in the same location in each matrix to form a new matrix with the same dimensions as the original matrices. The resulting matrix will have each element equal to the difference of the corresponding elements from the original matrices.
How do you multiply a matrix by a scalar?
To multiply a matrix by a scalar, you simply multiply every element in the matrix by the scalar value. For example, if you have a matrix A and want to multiply it by the scalar k, you would multiply each element Aij in the matrix by k to get the resulting matrix A' = k * A.
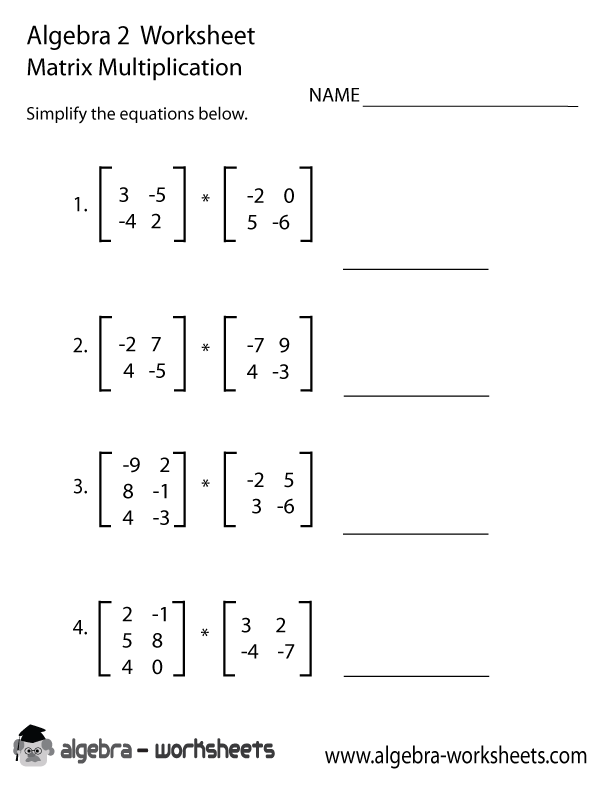
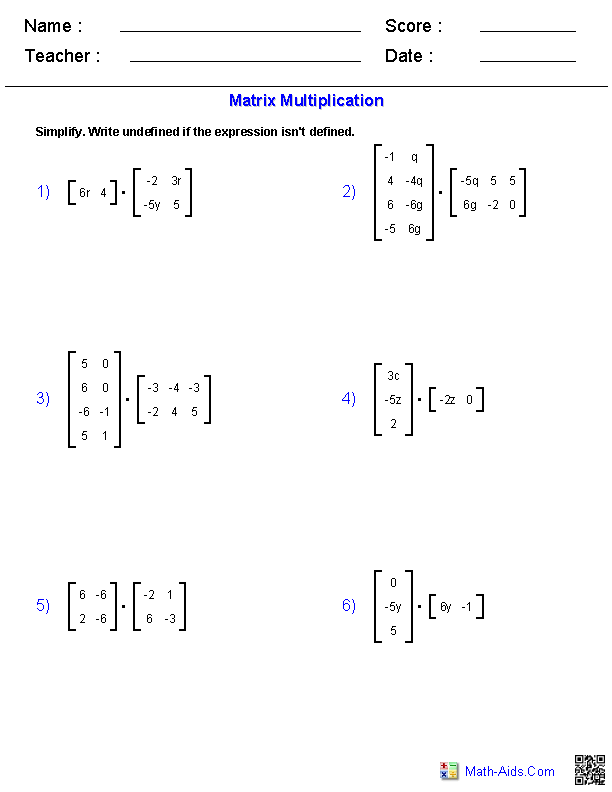
What is the matrix multiplication rule?
The matrix multiplication rule states that two matrices can be multiplied together if the number of columns in the first matrix is equal to the number of rows in the second matrix. When multiplying matrices A and B, the resulting matrix will have dimensions equal to the number of rows of A and the number of columns of B. The product of two matrices is found by taking the dot product of each row of the first matrix with each column of the second matrix.
How do you find the transpose of a matrix?
To find the transpose of a matrix, you simply switch its rows with columns. This means that the element at the ith row and jth column of the original matrix becomes the element at the jth row and ith column in the transposed matrix.
What are the properties of matrix addition, subtraction, and scalar multiplication?
Matrix addition follows the commutative and associative properties, meaning (A + B) = (B + A) and (A + B) + C = A + (B + C). Matrix subtraction is similar to addition, where (A - B) is equivalent to (A + (-B)). Scalar multiplication involves multiplying each element of a matrix by a constant scalar, preserving the properties of associativity and distributivity.
How do you solve a system of linear equations using matrix algebra?
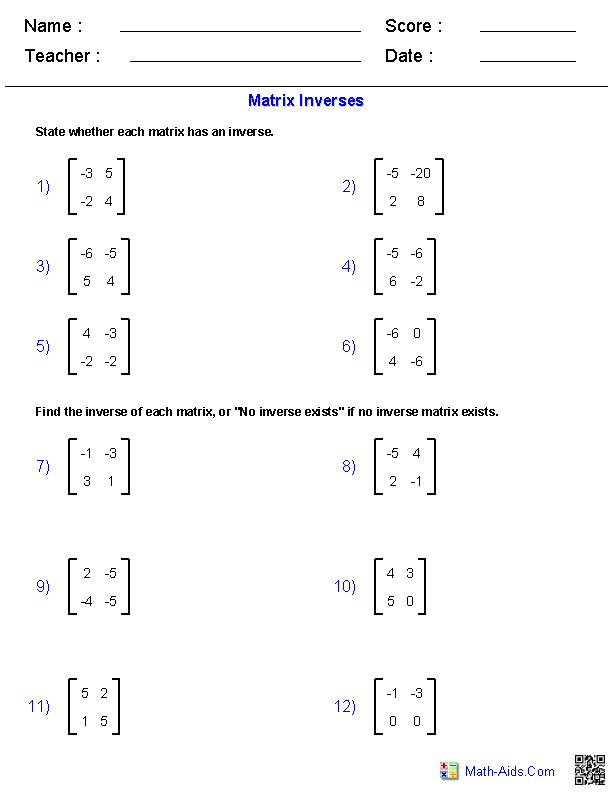
To solve a system of linear equations using matrix algebra, you first represent the system in matrix form by arranging the coefficients of the variables into a matrix, and the constants on the other side. Then, you calculate the inverse of the coefficient matrix using matrix algebra. Finally, you multiply the inverse of the coefficient matrix by the matrix containing the constants to obtain the values of the variables. This process allows you to efficiently solve the system of linear equations using matrix algebra.
How is matrix algebra used in real-life applications?
Matrix algebra is used in various real-life applications such as computer graphics for rendering images, in engineering for solving systems of equations, in financial modeling for analyzing stock market data, in statistics for data analysis and regression analysis, in physics for calculating forces and transformations, and in biological sciences for studying genetic inheritance patterns. Overall, matrix algebra provides a powerful tool for representing and solving complex problems in a wide range of fields.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.








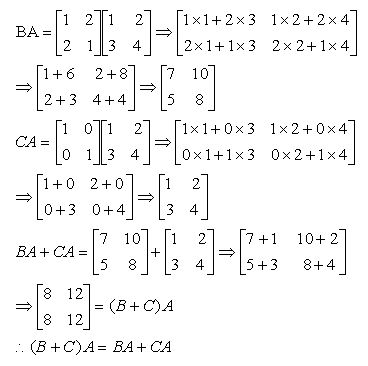


















Comments