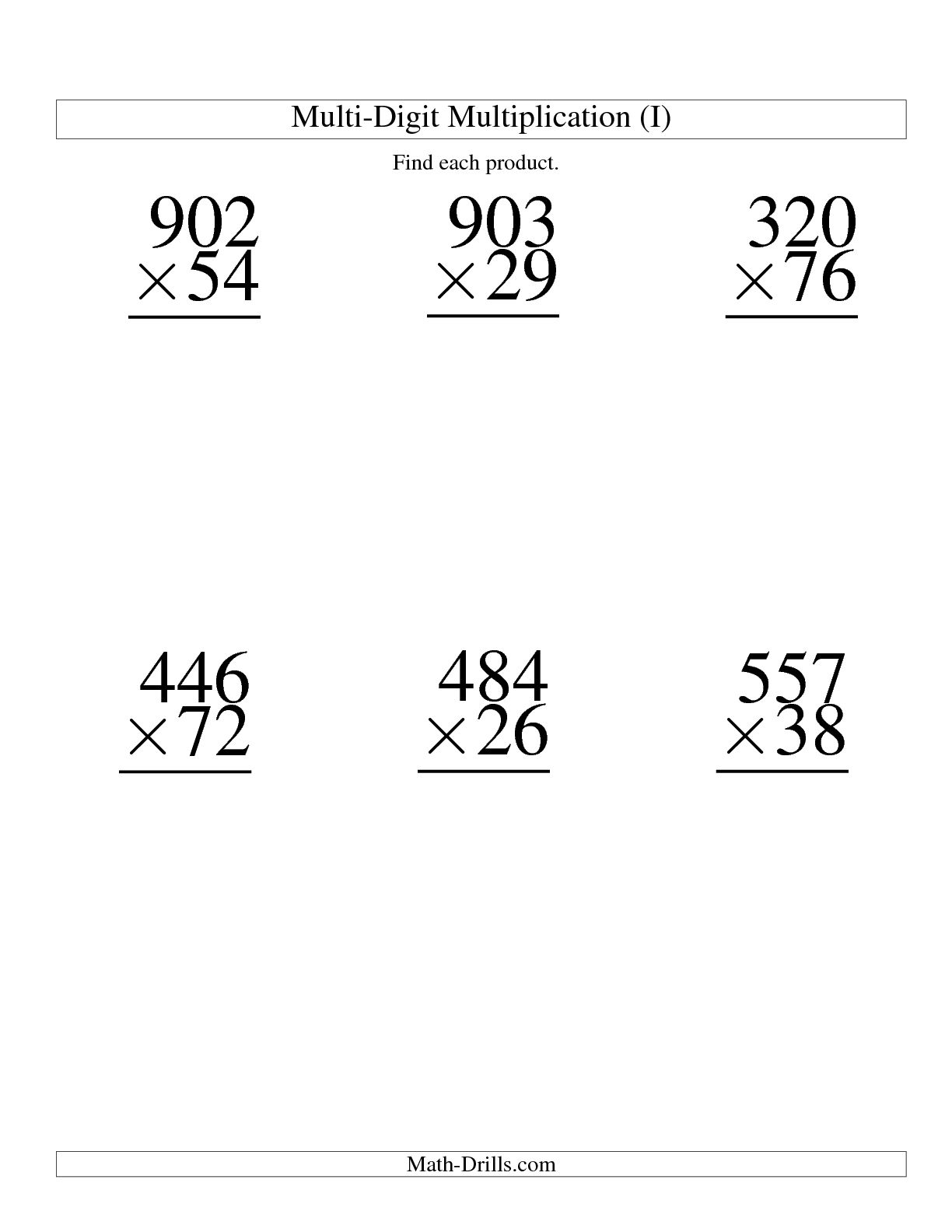
Math Three-Digit Multiplication Worksheets

Are you searching for a helpful tool to improve your math skills and master three-digit multiplication? Look no further! Our collection of three-digit multiplication worksheets is designed to provide a comprehensive and engaging learning experience for students who want to enhance their understanding of this mathematical concept.

  3-Digit Addition and Subtraction Worksheets

---

  Three-Digit Multiplication Worksheets

---

  3-Digit Addition with Regrouping

---

  Math Addition Worksheets

---

  2-Digit Multiplication Worksheets

---

  Math Addition Worksheets 2nd Grade

---

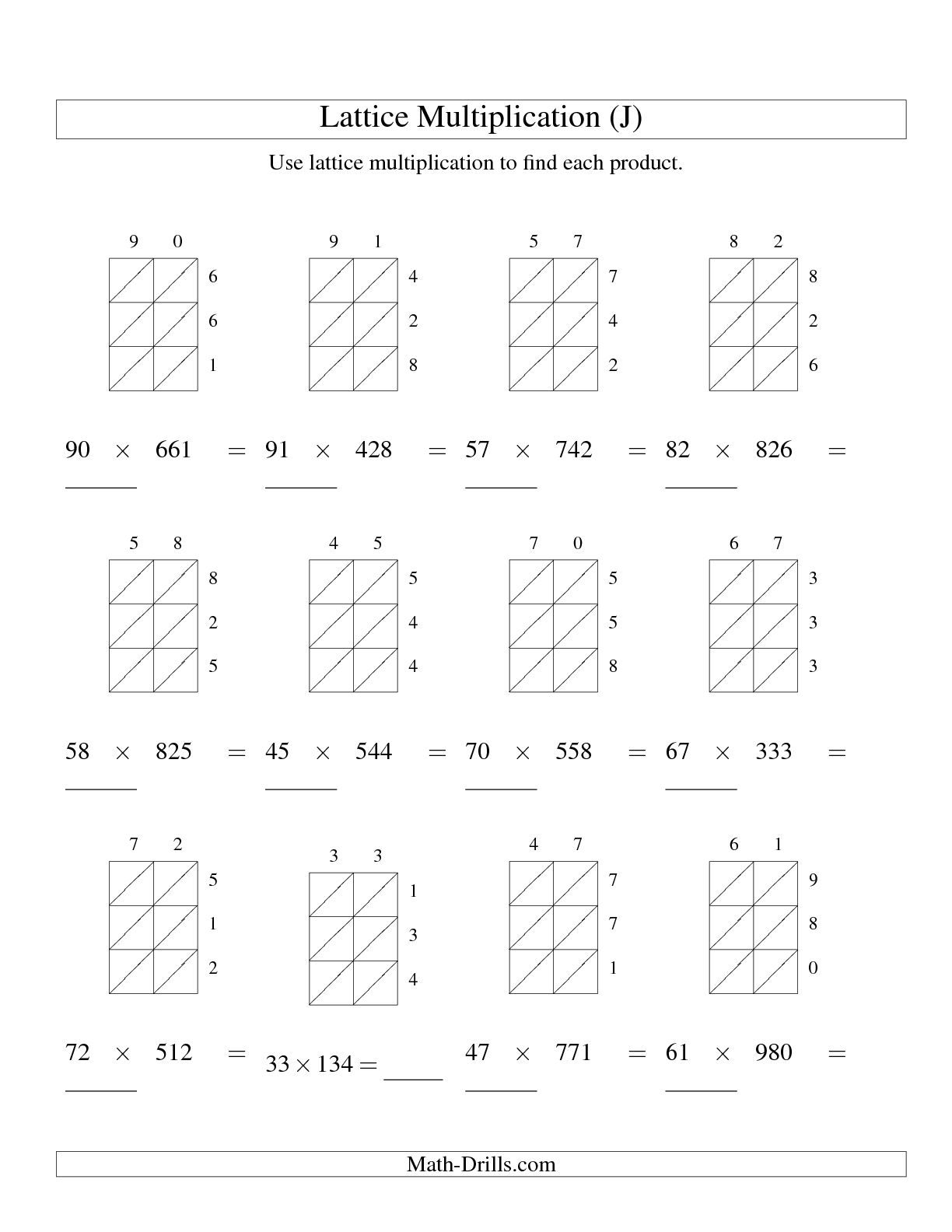
  Lattice Multiplication Worksheets

---

  2-Digit Multiplication Worksheets

---

  Addition with Regrouping Worksheets

---

  5th Grade Decimal Multiplication Worksheets

---

  4th Grade Math Word Problems Worksheets

---

  Addition Color by Number Coloring Pages

---

  Subtraction Across Zero Worksheets

---

  Math Addition Bingo Cards

---

  2-Digit Subtraction with Regrouping

---

  2-Digit Subtraction with Regrouping

---

What is the first step in three-digit multiplication?

The first step in three-digit multiplication is to multiply the ones digit of the top number by each of the digits in the bottom number, writing each product underneath the respective digit of the top number.

How can you ensure that you align the numbers correctly when multiplying three-digit numbers?

To ensure that you align the numbers correctly when multiplying three-digit numbers, line up the numbers carefully by placing the larger number on top and the smaller number on the bottom. Start by multiplying the ones digits first, then move on to the tens digits, and finally the hundreds digits. Make sure to write the products in the appropriate place value column, lining up the digits to avoid any confusion. Double-check your work to ensure accuracy and alignment throughout the multiplication process. Practice and attention to detail will help you become more proficient in aligning numbers correctly when multiplying three-digit numbers.

What is the process of multiplying the units digit of the ones column?

When multiplying the units digit of numbers in the ones column, you first multiply the units digits together. If the product is a single-digit number, you write it in the ones column of the final answer. If the product is a two-digit number, you write the units digit in the ones column of the final answer and carry over the tens digit to the next column to the left. This process continues as you move to the left across the columns in the multiplication.

How do you carry over a digit when multiplying the tens column in three-digit multiplication?

When multiplying the tens column in three-digit multiplication, if the product of the digits exceeds 9, you carry over the extra value by adding it to the product of the digits in the next column to the left. Place the digit in the ones place of the product and carry over the digit in the tens place to the next column. This helps you keep track of the correct value as you multiply larger numbers.

What is the purpose of placing a zero in the tens column when multiplying the hundreds column?

Placing a zero in the tens column when multiplying the hundreds column is done to correctly represent the place value progression in a multi-digit multiplication problem. By shifting the multiplication one place to the left and adding the zero, it ensures that the final product reflects the appropriate place value of the calculated product when multiplying larger numbers.

How do you multiply the hundreds column in three-digit multiplication?

To multiply the hundreds column in three-digit multiplication, you simply multiply the hundreds digit of the top number by each digit of the bottom number, placing the resulting product in the appropriate place value column. It is essential to remember to account for any carries when adding the products together with the other columns during the multiplication process.

What is the rule for placing the intermediate products in the correct position during three-digit multiplication?

When multiplying three-digit numbers, the rule for placing the intermediate products in the correct position is to align each product in the same column as the digit it represents in the original multiplication problem. Start by multiplying the ones digit of the bottom number with each digit of the top number, then the tens digit, and finally the hundreds digit. Make sure to properly shift the products one position to the left for each successive multiplication. Keep track of the carryovers from each column to the next until all multiplications are completed, and then add up the results to get the final product.

What is the final step in three-digit multiplication?

The final step in three-digit multiplication is adding together all the partial products obtained from multiplying the single digit of the second number by each digit of the first number, making sure to align the numbers properly and carry over any extra tens if necessary to get the final product of the multiplication.

How do you perform a quick check to verify the accuracy of your three-digit multiplication?

To perform a quick check on the accuracy of your three-digit multiplication, you can estimate the answer by rounding the numbers to the nearest tens or hundreds and then multiplying them. Compare this estimate with the actual result you obtained from the multiplication to see if they are in the same ballpark. Additionally, you can perform the multiplication in reverse by dividing the product by one of the factors to check if it matches the other factor.

Can you provide an example of a three-digit multiplication problem with step-by-step explanation?

Sure! Let's multiply 324 by 567. First, write down the numbers vertically, with the larger number on top. Next, multiply 4 (units place) in 324 by 7 (units place) in 567, which gives 28. Write down 8 and carry over 2. Then, multiply 4 by 6, add the carried over 2, and write down 26. Continue this process for 2 (tens place) and 3 (hundreds place) in 324 with 5 and 6 in 567, then add up the results to get the final answer of 183,768.