Math Slope Worksheets

Slope worksheets are an invaluable resource for students looking to solidify their understanding of this fundamental concept in math. These worksheets provide a structured and comprehensive approach to learning about slope, making it easier for students to grasp the concept and apply it to various real-world scenarios. Whether you are a middle school student looking to strengthen your foundation or a high schooler aiming to ace your exams, these slope worksheets are specifically designed to cater to your needs and help you excel in your math education.

  7th Grade Math Inequalities Worksheets Printable

---

  Printable Slope Worksheets 8th Grade

---

  First Grade Fraction Worksheets

---

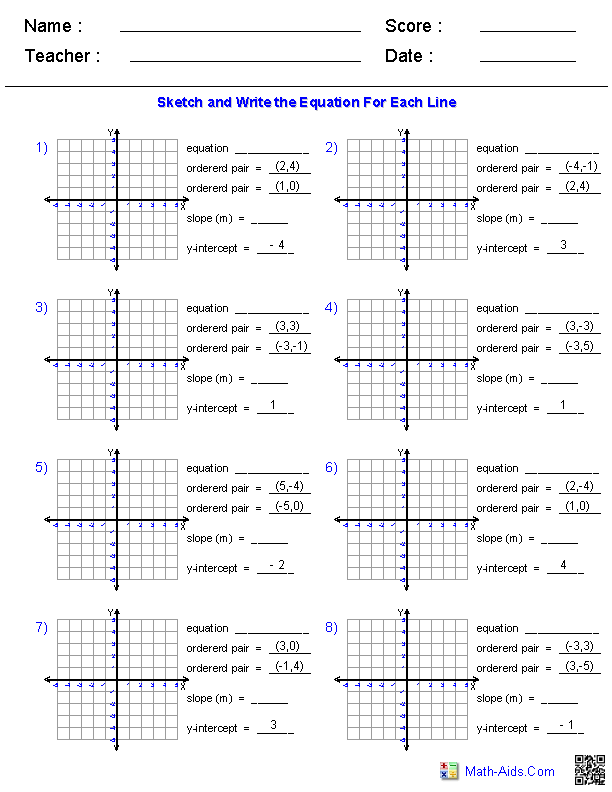
  Slope-Intercept Form Worksheet

---

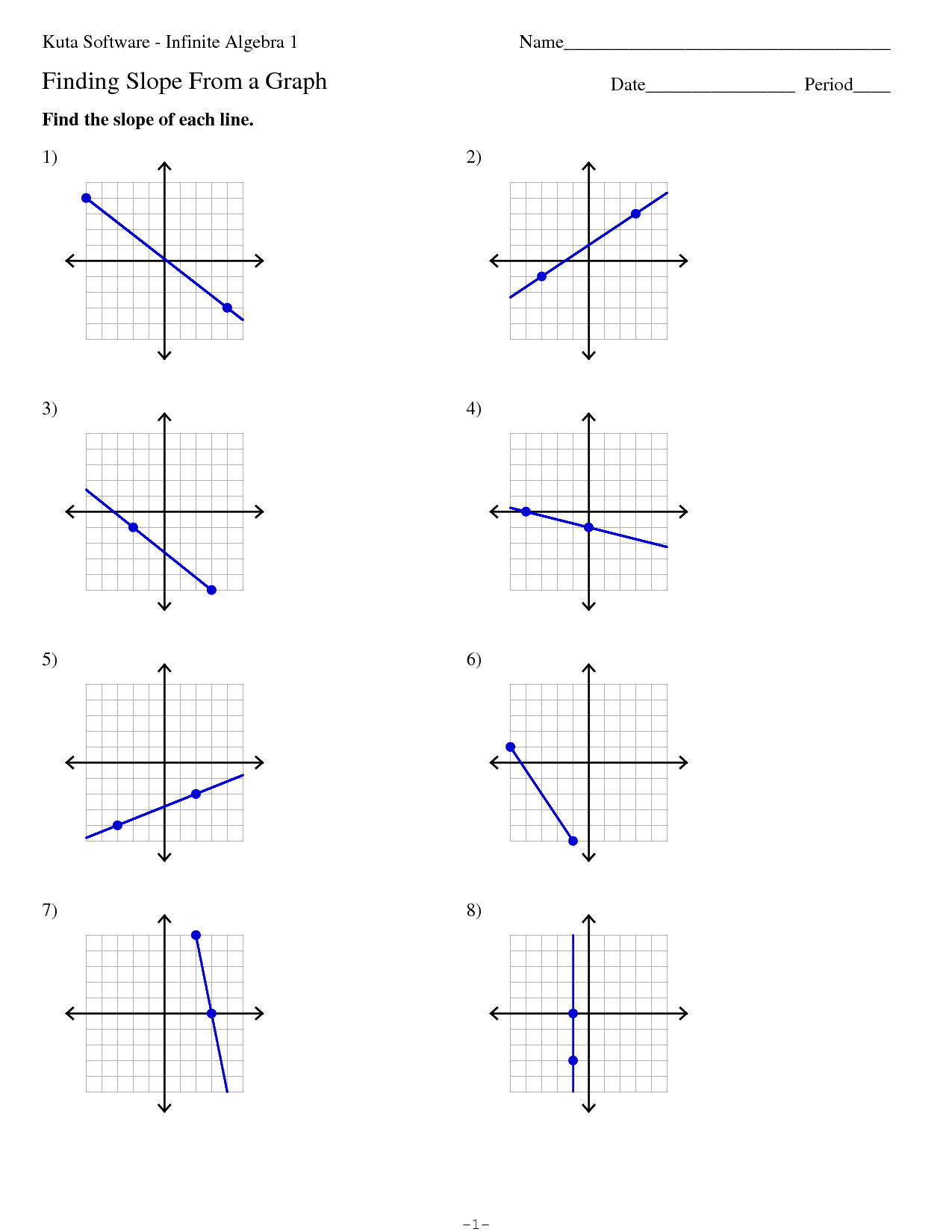
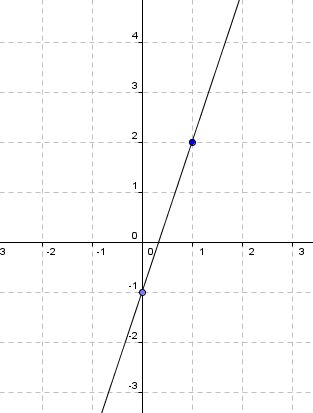
  Kuta Software Infinite Algebra 1 Finding Slope From a Graph

---

  3rd Grade Math Worksheets Decimals

---

  Slope-Intercept Word Problems Worksheet

---

  Graphing Using Slope-Intercept Form Worksheet

---

  Write Each Line From the Equation Worksheet

---

  Algebraic Expressions Worksheets

---

  Math Addition Worksheets 2nd Grade

---

What is the slope of a horizontal line?

The slope of a horizontal line is 0.

How would you find the slope of a vertical line?

A vertical line has an undefined slope because it does not have a change in the y-coordinate for any change in the x-coordinate. The equation for a vertical line is x = constant, and since the slope is the change in y divided by the change in x, and in this case, there is no change in x, the slope is undefined.

How do you calculate the slope between two points on a coordinate plane?

To calculate the slope between two points on a coordinate plane, you can use the formula: slope = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of the two points. Subtract the y-coordinates and x-coordinates of the points, then divide the difference in y-coordinates by the difference in x-coordinates to determine the slope.

Can the slope be negative? Why or why not?

Yes, the slope of a line can be negative. The slope of a line represents the rate of change of the dependent variable with respect to the independent variable. A negative slope indicates that as the independent variable increases, the dependent variable decreases. This is a common occurrence in various real-world scenarios and is perfectly valid in mathematical calculations.

What does a slope of zero indicate about a line?

A slope of zero indicates that the line is horizontal, which means it is perfectly flat and does not rise or fall as it extends. This means that for every change in the x-coordinate, the y-coordinate remains the same, resulting in a straight line that runs parallel to the x-axis.

How does the slope of a line relate to its steepness?

The slope of a line indicates its steepness. A greater slope value represents a steeper line, while a smaller slope value represents a less steep line. For instance, a line with a slope of 2 is steeper than a line with a slope of 0.5. The slope is calculated as the change in the y-coordinate divided by the change in the x-coordinate between two points on the line, which directly influences how steep the line appears.

How can you determine if two lines are parallel based on their slopes?

If two lines have the same slope, then they are parallel. This is because lines with the same slope will have the same steepness or direction, resulting in them never intersecting and running side by side.

How can you determine if two lines are perpendicular based on their slopes?

Two lines are perpendicular if the product of their slopes is -1. In mathematical terms, if the slope of one line is m1 and the slope of another line is m2, then they are perpendicular if m1 x m2 = -1. This is a property of perpendicular lines in Euclidean geometry.

What is the slope of a line that goes through two points with the same x-coordinate?

The slope of a line that goes through two points with the same x-coordinate is undefined. This is because the slope of a line is determined by the change in the y-coordinates divided by the change in the x-coordinates, and if the x-coordinates are the same, the denominator becomes 0, leading to an undefined value for the slope.

How can you interpret the slope of a line in real-life scenarios?

The slope of a line represents the rate of change between two variables, therefore in real-life scenarios, it can indicate the speed of change or the relationship between two quantities. For example, if the slope of a distance-time graph is steep, it indicates a fast speed, while a shallower slope suggests a slower speed. In financial terms, the slope of a line can represent the rate of return on an investment or the cost increase over time. Generally, a positive slope indicates an increase in one variable as the other increases, while a negative slope suggests the decrease of one variable as the other increases.