Math Functions Worksheets
Math functions worksheets are a valuable resource for students who are looking to strengthen their understanding of mathematical concepts. These worksheets provide a structured and organized way to practice various mathematical functions, such as addition, subtraction, multiplication, and division. By utilizing math functions worksheets, students can enhance their ability to comprehend and apply these fundamental mathematical operations.
Table of Images 👆
- Function Tables Worksheets
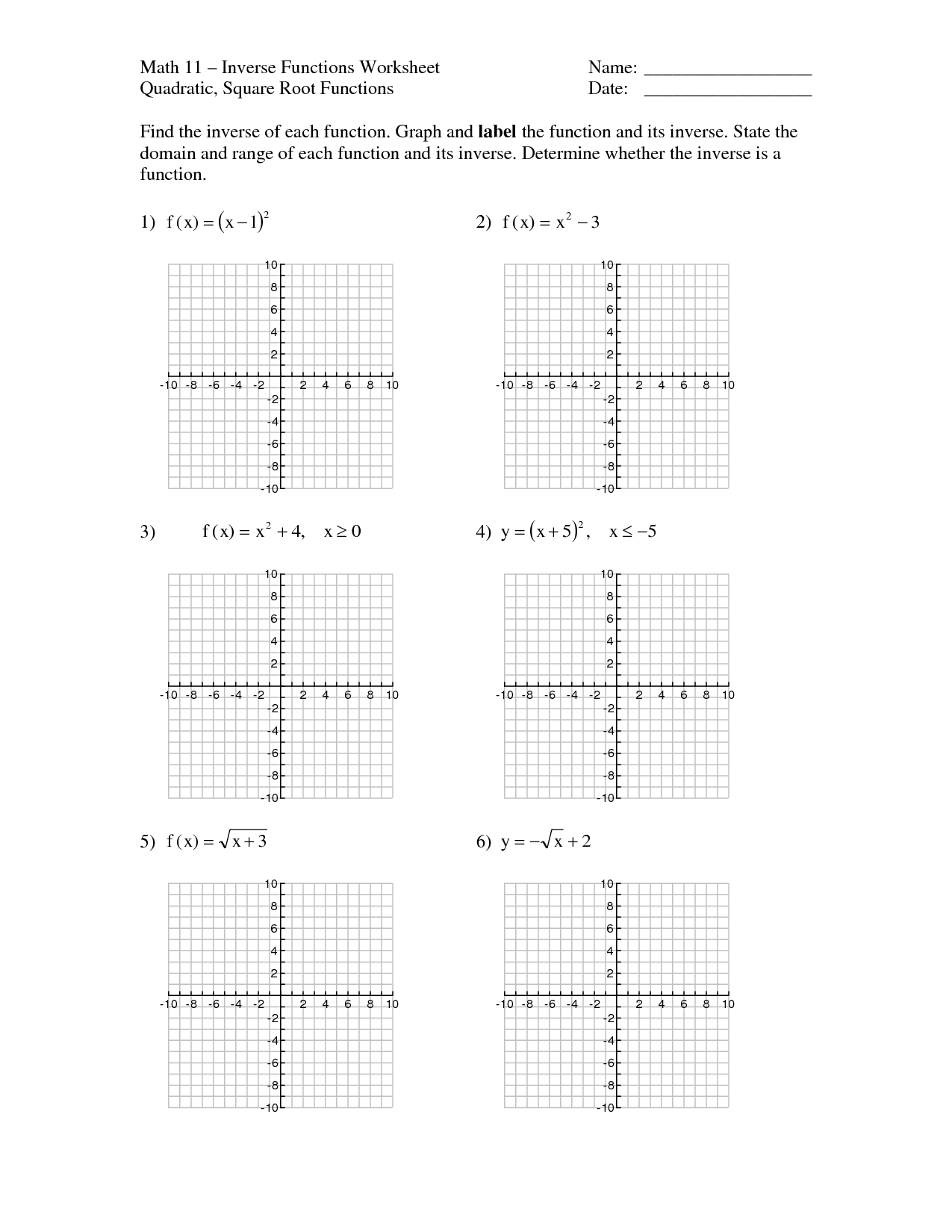
- Graph Inverse Functions Worksheet
- Exponents
- Math Worksheets Inverse Functions
- Function Notation Worksheet
- Algebra 1 Worksheets
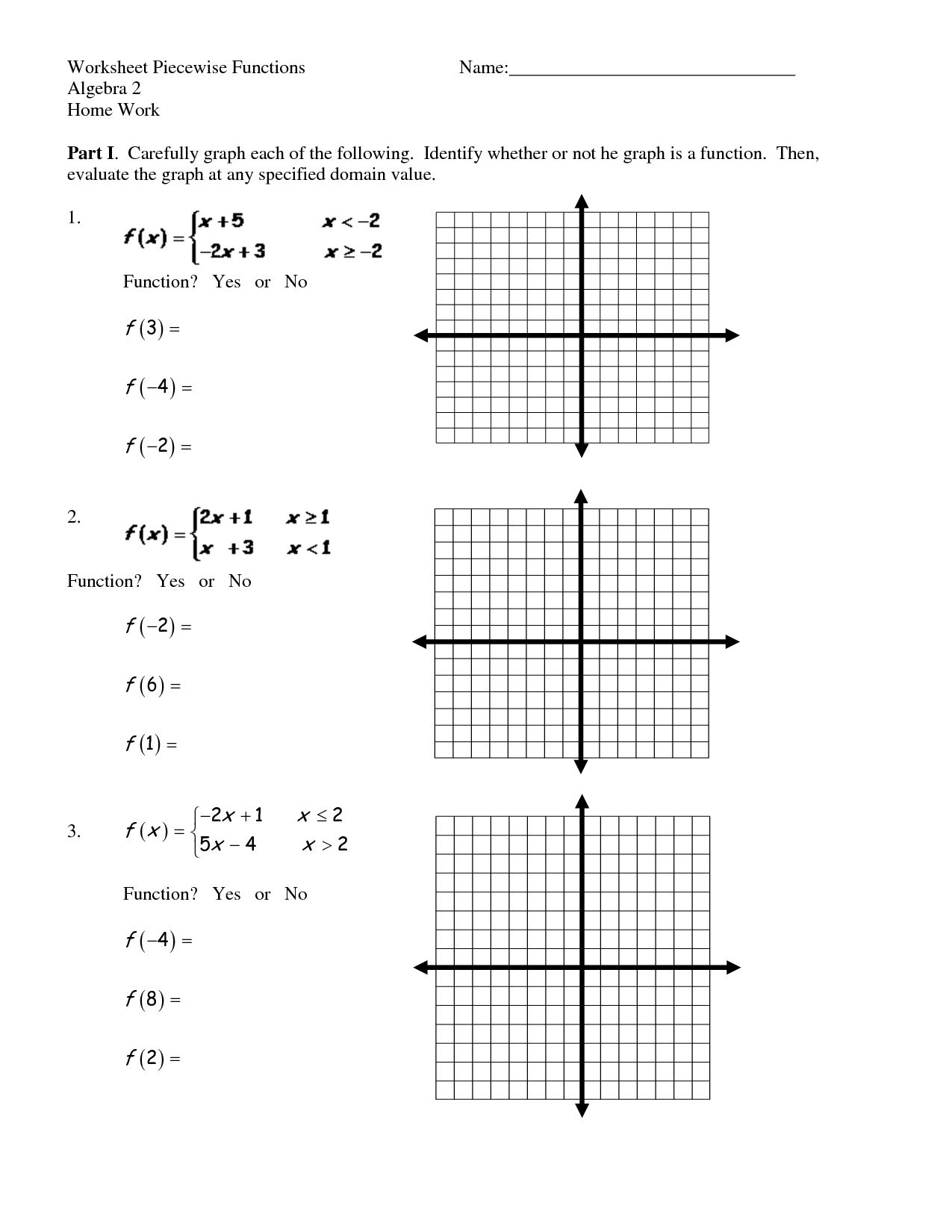
- Algebra 2 Piecewise Function Worksheets
- Quadratic Functions Worksheet
- Function Notation Algebra 1 Worksheet Answers
- Algebra 2 Function Operations Worksheet
- Function Transformation Worksheet
- Function Notation Algebra Worksheets
- Graphing Exponential Functions Worksheets
More Math Worksheets
Printable Math WorksheetsMath Worksheets Printable
Printable Math Worksheets Multiplication
Math Worksheets for 2nd Graders
Math Practice Worksheet Grade 6
Math Multiplication Worksheets
First Grade Subtraction Math Worksheets Printable
Rocket Math Practice Worksheets
Math Worksheets Integers
Superhero Math Worksheets
What is a math function?
A math function is a rule or correspondence that assigns each element in one set (called the domain) to a unique element in another set (called the range) such that each input has exactly one output. It describes a relationship between elements of sets, usually represented by an equation or formula, and can be used to model various mathematical relationships and phenomena.
How do you represent a math function?
A math function can be represented using an equation that relates one set of values (inputs) to another set of values (outputs). This equation typically uses variables to represent the input and output values, along with mathematical operations such as addition, subtraction, multiplication, division, exponentiation, or trigonometric functions. The function can be written in various forms, such as algebraic expressions, graphs, tables, or verbal descriptions, depending on the context and purpose of the representation.
What are the different types of functions?
There are several types of functions in mathematics, including linear functions, quadratic functions, polynomial functions, exponential functions, logarithmic functions, trigonometric functions, and rational functions. Each type of function has a specific form and behavior when graphed, and they are used to model various real-world phenomena and solve mathematical problems.
How do you determine the domain and range of a function?
To determine the domain of a function, you consider what values of the independent variable (input) are allowed. The domain consists of all possible input values that produce a valid output. To find the range, you look at the set of all possible output values that the function can produce based on the given domain. This involves evaluating the function for different input values to see the corresponding output values. The range represents the set of all possible output values that the function can attain.
What is the difference between a linear and nonlinear function?
A linear function represents a straight line graph and has a constant rate of change, while a nonlinear function does not follow a straight line graph and has a varying rate of change. Linear functions have a constant slope and can be expressed in the form of y = mx + b, where m is the slope and b is the y-intercept. Nonlinear functions, on the other hand, have a curved or non-constant graph shape and cannot be directly represented with a simple equation in the form of y = mx + b.
How do you find the slope of a linear function?
To find the slope of a linear function, you can choose any two points on the line and use the formula: slope = (change in y) / (change in x), which is calculated by subtracting the y-coordinates of the two points and dividing by the difference in their x-coordinates. Alternatively, if you have the equation of the linear function in the form y = mx + b, where m is the slope, then you can determine the slope directly from the equation.
What is the intercept of a linear function?
The intercept of a linear function is the point at which the function intersects the y-axis. It is the value of y when x is equal to zero. The intercept is an important characteristic of a linear function as it helps in determining the behavior and position of the function on a graph.
How do you graph a quadratic function?
To graph a quadratic function, start by plotting the vertex, which is the point where the parabola changes direction. Then, use the axis of symmetry, which is the vertical line passing through the vertex, to plot other points on the graph. Next, plot additional points based on the symmetry of the parabola. If the quadratic function opens upwards, continue extending the parabola outward in both directions. If the quadratic function opens downwards, do the same but downwards. Finally, connect the points to form a smooth curve that represents the graph of the quadratic function.
What are the key characteristics of exponential functions?
Exponential functions are characterized by having a constant base raised to a variable exponent, typically written as f(x) = a^x. They grow exponentially, meaning the rate of increase gets larger as x increases. They have a y-intercept at (0,1) if a>0 and a≠1, and they never cross the x-axis. Exponential functions exhibit rapid growth or decay, depending on whether the base is greater than 1 (growth) or between 0 and 1 (decay). They are commonly used to model phenomena such as population growth, compound interest, and radioactive decay.
How do you solve equations involving trigonometric functions?
To solve equations involving trigonometric functions, you typically isolate the trigonometric function by applying inverse trigonometric functions or trigonometric identities as needed. You might need to use algebraic manipulation techniques to simplify the equation and make it easier to solve. It's important to pay attention to common trigonometric identities and properties to help you solve the equation step by step until you find the solutions within the specified domain.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.






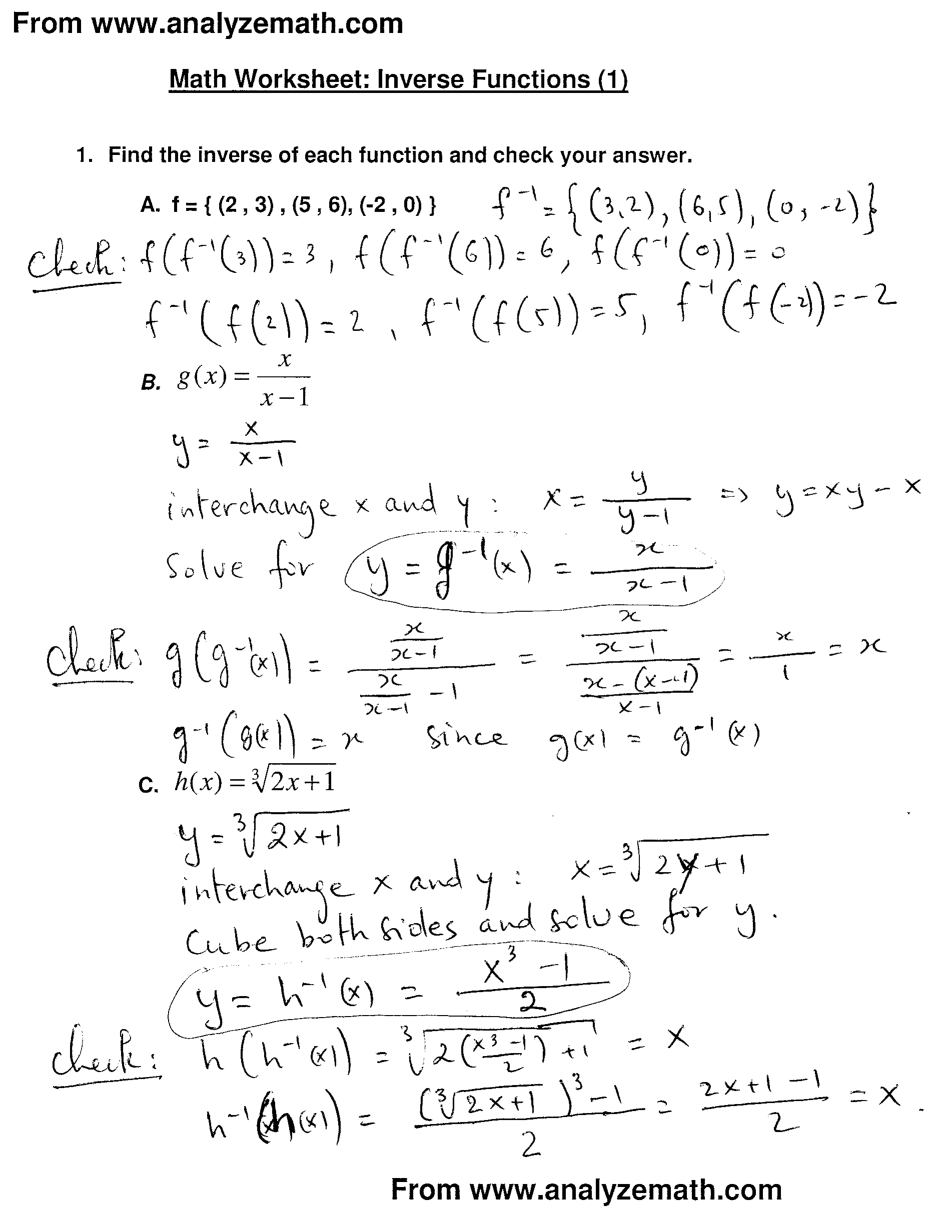





















Comments