Linear Programming Worksheet

Linear programming is a valuable tool in solving various optimization problems. Whether you are a student studying operations research or a professional looking to improve decision-making processes, a well-structured and comprehensive worksheet can help you grasp the concepts and practice the techniques associated with linear programming.

  Graphing Linear Inequalities Worksheet

---

  Graphing Inequalities On a Number Line Worksheets

---

  Linear Equation Word Problems Worksheet

---

  Graphing Linear Inequalities Worksheet

---

  Linear Programming Worksheets with Answers

---

  Linear Programming Examples

---

  Graphing Linear Inequalities Worksheet Answers

---

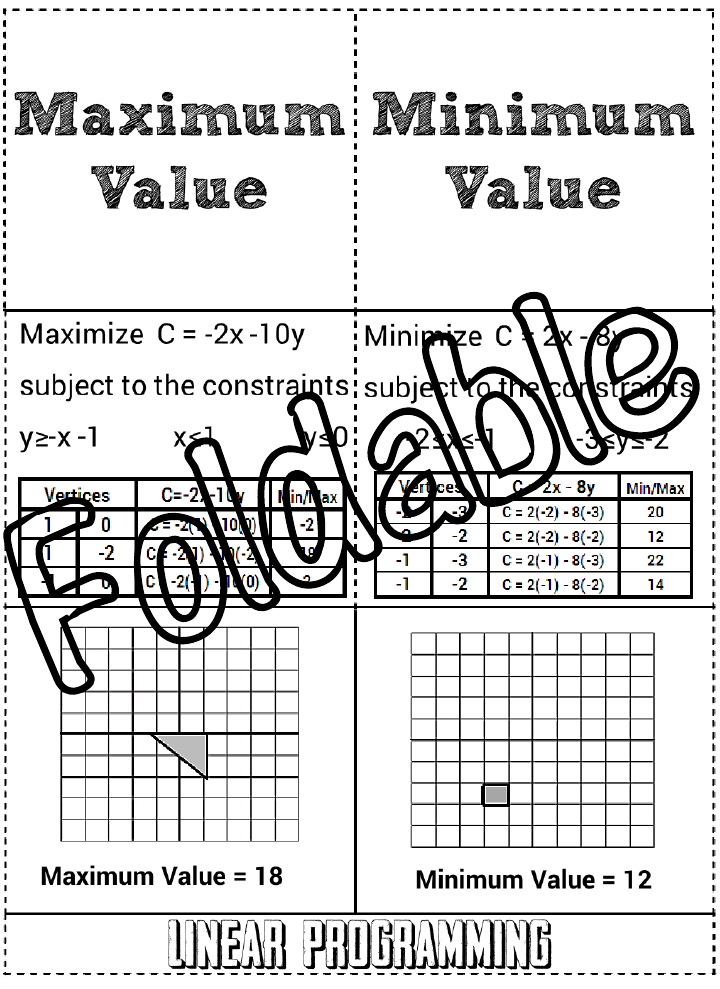
What is Linear Programming?

Linear Programming is a mathematical method used to find the best outcome in a set of linear equations that represent constraints and an objective function. It involves maximizing or minimizing a linear objective function subject to linear equality and inequality constraints. It is widely used in various fields such as economics, business, engineering, and logistics to optimize resource allocation and decision-making processes.

What are the main components of a linear programming problem?

The main components of a linear programming problem include decision variables (representing unknown quantities to be determined), objective function (to be optimized such as maximizing profit or minimizing cost), constraints (limitations or restrictions on the decision variables), and non-negativity restrictions (requirements that the decision variables must be greater than or equal to zero). By combining these components, linear programming helps in finding the best possible solution to a mathematical model within defined constraints.

What is an objective function?

An objective function is a mathematical function that represents the goal or target to be optimized in an optimization problem. It quantifies the performance of a solution and is used to determine the best solution among a set of feasible alternatives. The objective function can be maximized (optimization problems seeking to maximize a parameter such as profit) or minimized (optimization problems seeking to minimize a parameter such as cost).

What are decision variables?

Decision variables are the variables in a mathematical model that represent choices or decisions that need to be made in order to optimize a particular outcome. These variables are used to define the parameters and constraints of the model, and their values are determined based on the specific problem being analyzed. In operations research and optimization problems, decision variables are used to quantify the decision-making process and find the best course of action.

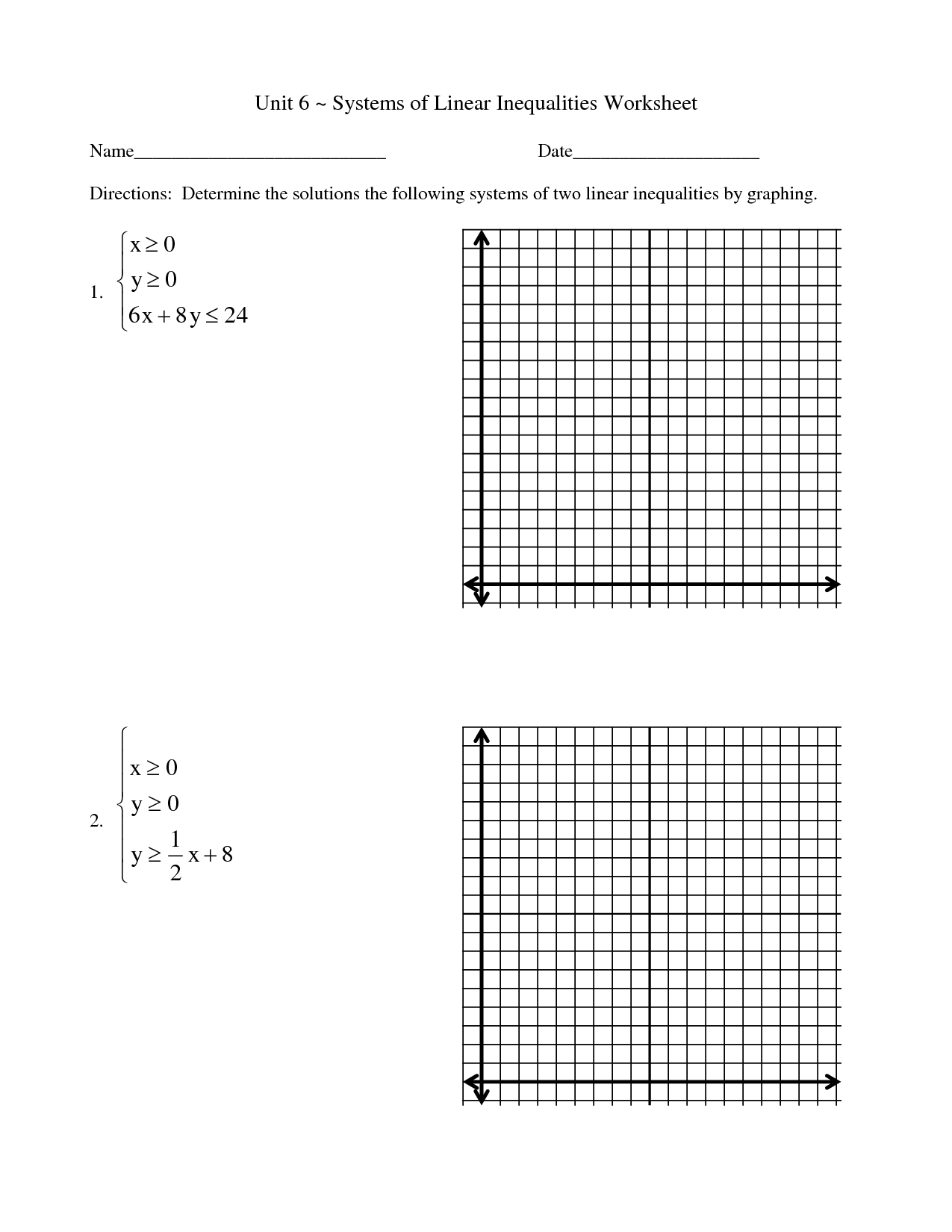
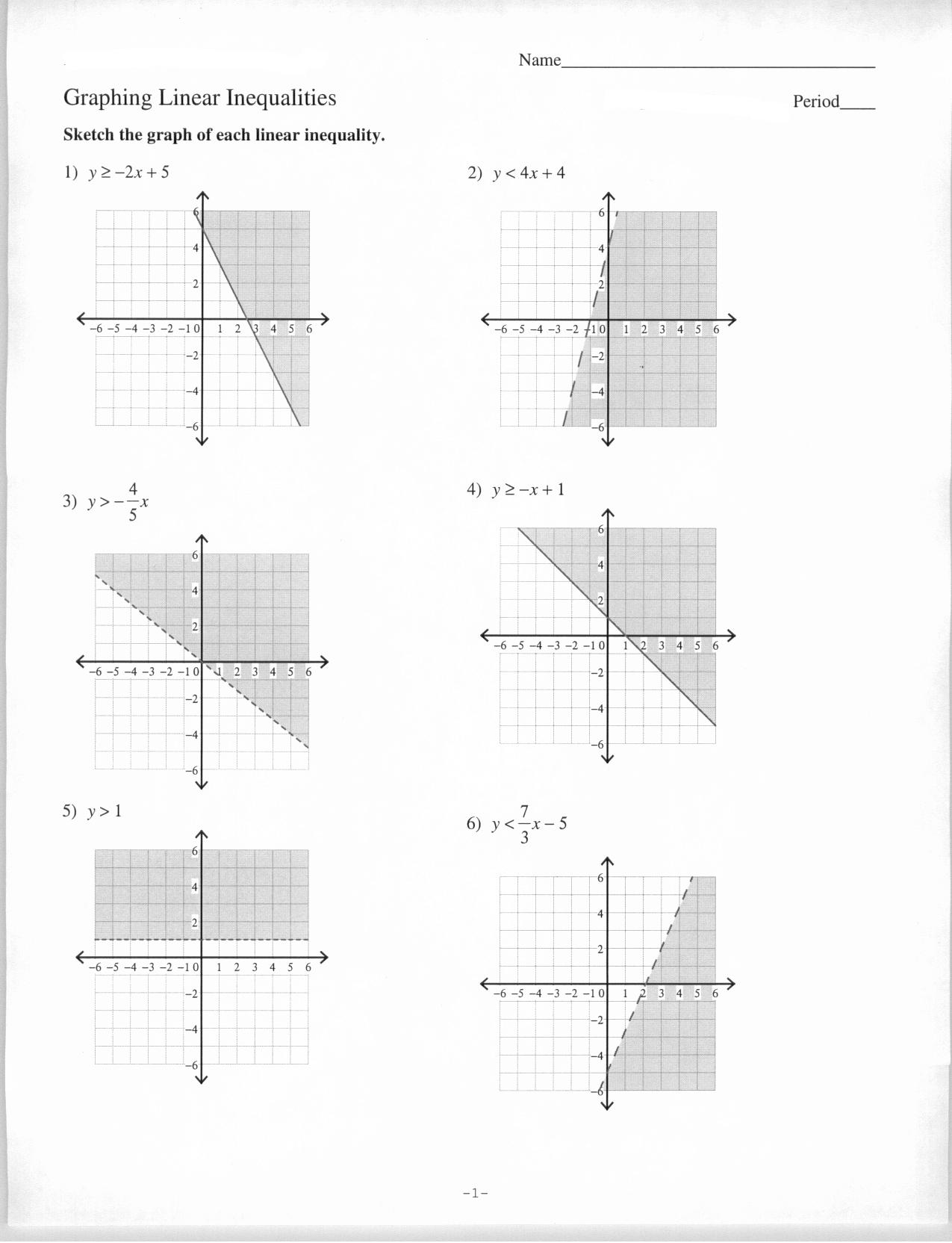
Can constraints in linear programming be expressed using inequalities?

Yes, constraints in linear programming are often expressed using inequalities. These inequalities represent restrictions on the feasible solutions that can be considered in the optimization problem. These constraints help define the boundaries within which the solution must lie, allowing the linear programming algorithm to find the optimal solution.

What is the feasible region in linear programming?

The feasible region in linear programming is the set of all possible solutions that satisfy all the constraints of the problem, including non-negativity constraints. It is the region of the graph where the feasible solutions lie, and the optimal solution will typically be found within this region. The feasible region is defined by the intersection of the constraints, representing the feasible values for the decision variables that optimize the objective function.

What is the optimal solution in linear programming?

The optimal solution in linear programming is the combination of decision variables that results in the maximum (or minimum) value of the objective function, while satisfying all the constraints. This solution provides the best outcome for the problem at hand and can be determined using various optimization techniques such as the Simplex method or the graphical method.

How is the graphical method used to solve linear programming problems?

The graphical method is used to solve linear programming problems by visually representing the constraints and objective function on a graph in order to identify the feasible region, which is where all constraints are satisfied. By plotting the constraints as inequalities on the graph and finding the region that satisfies all constraints, the optimal solution can be found at the point where the objective function is maximized or minimized within the feasible region. This method provides a clear and intuitive way to understand and solve linear programming problems with two decision variables.

What is the difference between a bounded and an unbounded solution in linear programming?

In linear programming, a bounded solution refers to a feasible region where the optimal solution exists within a defined and limited range of values for the decision variables. On the other hand, an unbounded solution occurs when the objective function can be increased or decreased indefinitely without reaching an optimal solution due to the absence of constraints that limit the feasible region, leading to no finite optimal solution.

How can sensitivity analysis help in understanding a linear programming problem?

Sensitivity analysis in linear programming can help in understanding the impact of changes in input parameters or coefficients on the optimal solution. By performing sensitivity analysis, you can identify how changes in the constraints, objective function coefficients, or resource availability affect the optimal solution, providing insights into the robustness and stability of the solution. This analysis can help decision-makers make informed choices by understanding the range of values within which the optimal solution remains valid and reliable, ultimately enhancing the understanding and management of the linear programming problem.