Inverse Trigonometry Functions Worksheets

Inverse trigonometry functions can be a challenging topic for math students. Understanding how to work with these functions and their properties is crucial for success in higher-level mathematics courses. If you're a student who is struggling with inverse trigonometry functions or a teacher looking for additional resources to reinforce these concepts, these worksheets can be a helpful tool.

  Right Triangle Trigonometry Worksheet Answers

---

  Basic Trig Functions Worksheet

---

  Graph Trig Functions Worksheet

---

  Graphing Trig Functions Worksheet

---

  Math Properties Worksheets 6th Grade

---

  Y 1 2X 2 Slope-Intercept Form

---

  Reflection On Grid

---

What is the definition of an inverse trigonometry function?

An inverse trigonometry function is a function that reverses the operation of a trigonometric function. It is used to find the angle measure given the value of the trigonometric ratio. The inverse trigonometry functions are denoted by the prefix "arc" or "a" (e.g., arcsin, arccos, arctan).

How are inverse trigonometry functions related to regular trigonometry functions?

Inverse trigonometry functions are related to regular trigonometry functions by undoing the operations of trigonometry functions. They are used to find the angle that corresponds to a given trigonometric ratio. For example, while the sine function determines the ratio of the length of the opposite side to the hypotenuse in a right triangle, the inverse sine function (sin^-1) will give you the angle when you know those lengths. In essence, inverse trigonometry functions provide a way to find angles based on trigonometric ratios, offering a different perspective on the information provided by regular trigonometry functions.

What are the six main inverse trigonometry functions?

The six main inverse trigonometric functions are arcsin (inverse sine), arccos (inverse cosine), arctan (inverse tangent), arccsc (inverse cosecant), arcsec (inverse secant), and arccot (inverse cotangent).

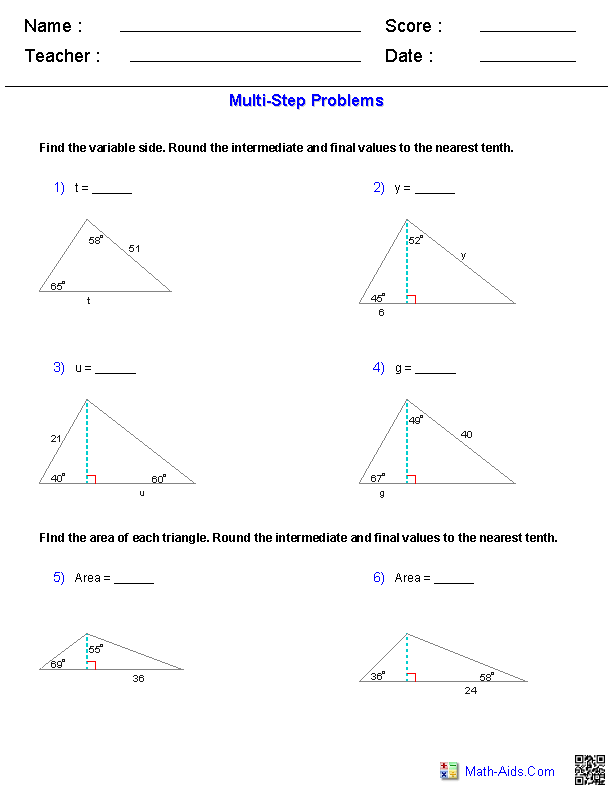
How do you find the inverse of a trigonometry function algebraically?

To find the inverse of a trigonometry function algebraically, you typically start by setting the function equal to y, then switch the roles of x and y. Next, solve for the new y (now the inverse) in terms of x, keeping in mind the restricted domain of the original function to ensure that the inverse exists. This will provide you with the algebraic expression for the inverse of the trigonometry function.

What is the range of the inverse sine function?

The range of the inverse sine function, also known as arcsin, is between -?/2 and ?/2, inclusive, which means it can take on values from -90 degrees to 90 degrees.

What is the domain of the inverse cosine function?

The domain of the inverse cosine function, denoted as cos^(-1)(x) or arccos(x), is -1 ? x ? 1. This means that the input values for the inverse cosine function must be within the range of -1 to 1 in order for the function to be defined.

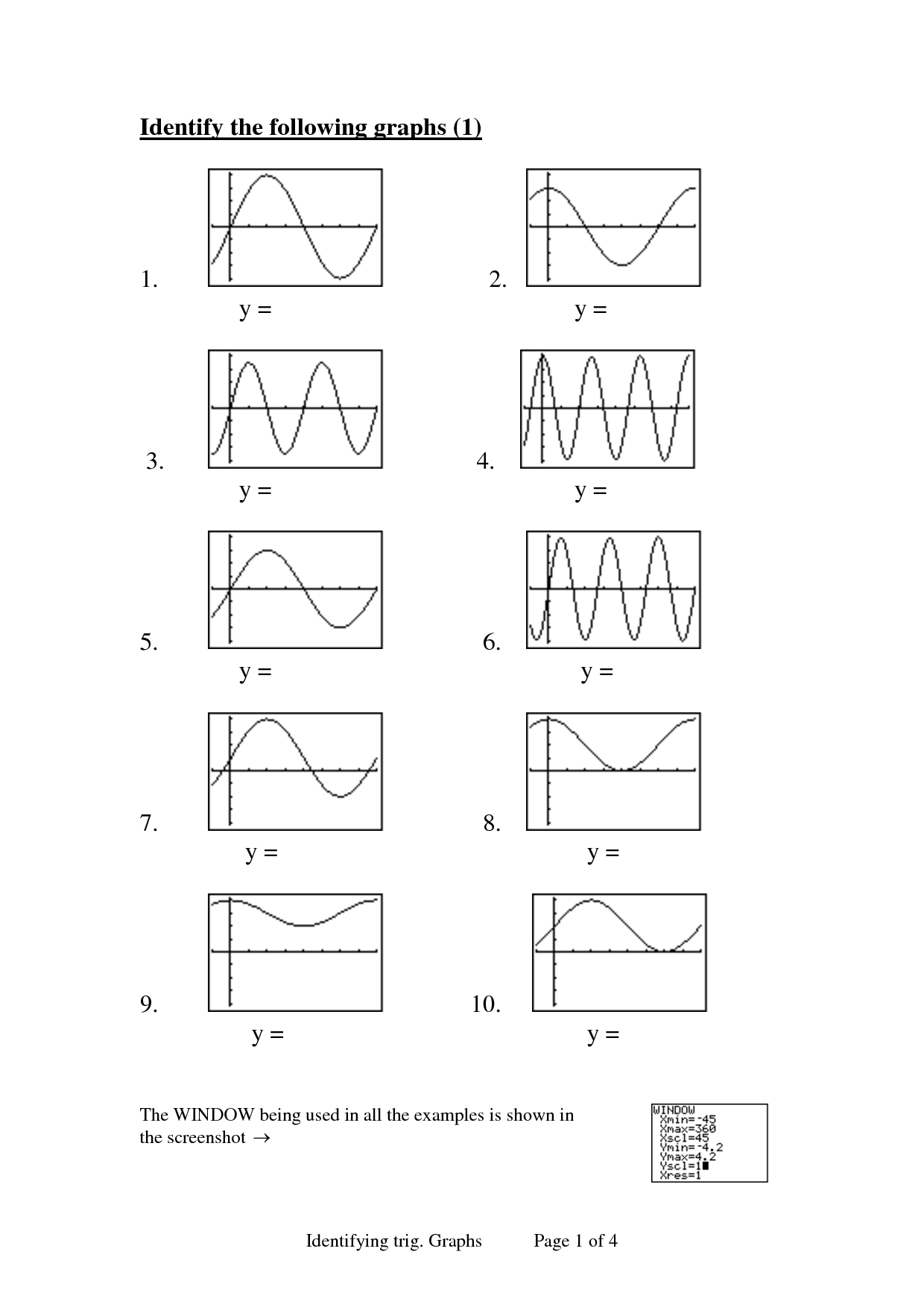
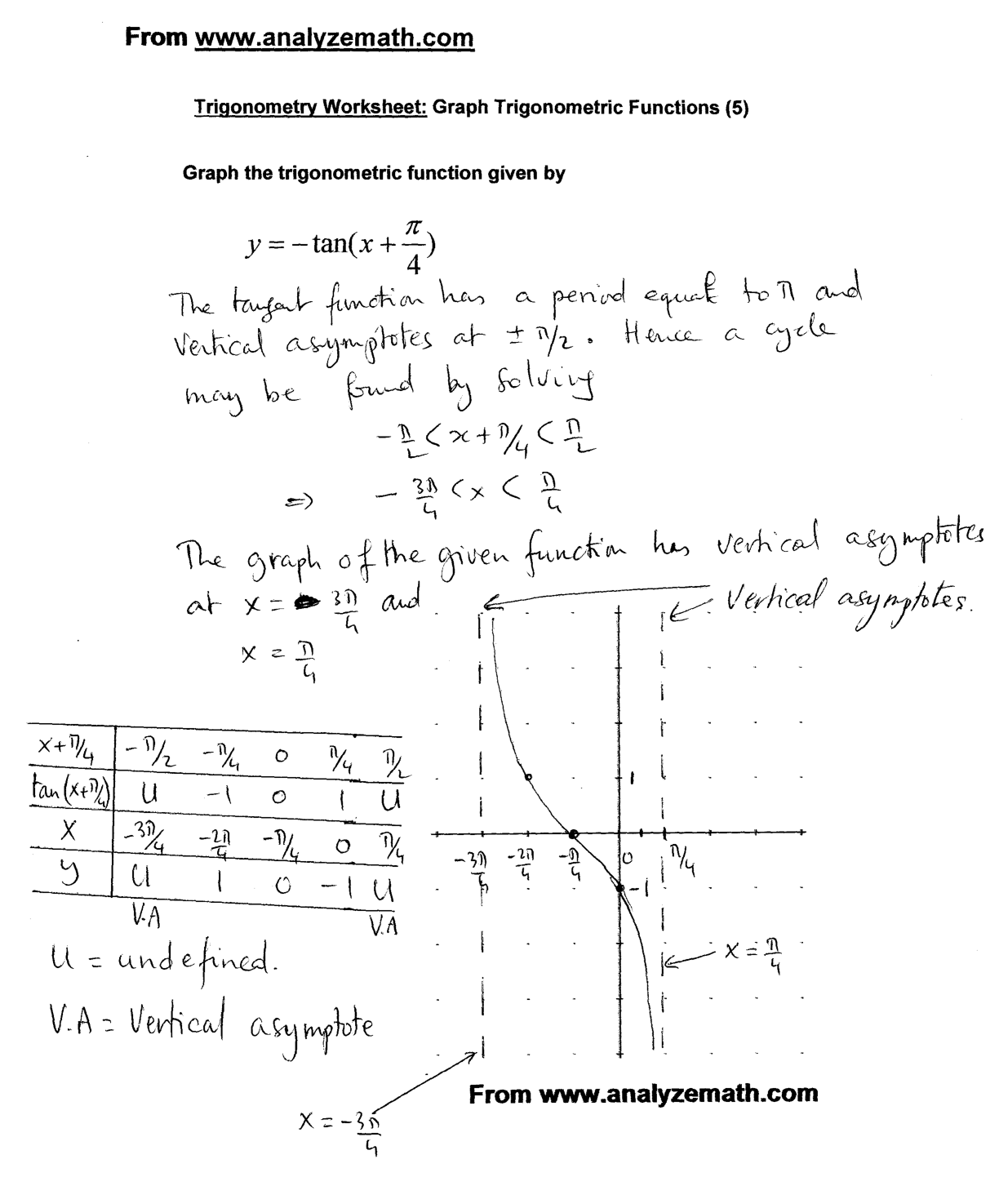
How do you graph the inverse tangent function?

To graph the inverse tangent function, first plot points by considering values of x between -?/2 and ?/2, since the domain of the inverse tangent function is (-?, ?) and the range is (-?/2, ?/2). Connect these points smoothly to form a curve that approaches the asymptotes at x = -?/2 and x = ?/2. This curve represents the graph of the inverse tangent function.

What is the derivative of the inverse cosecant function?

The derivative of the inverse cosecant function is equal to -1/(|x| * sqrt(x^2 - 1)), where x is the input variable in the domain of the function.

How are inverse trigonometry functions used in real-life applications?

Inverse trigonometry functions are used in various real-life applications such as in engineering for calculating angles, in physics for analyzing waveforms and oscillations, in navigation for determining distances and angles, in surveying for measuring heights and distances, in computer graphics for rendering shapes and animations, and even in music theory for analyzing harmonics and frequencies. These functions help in solving problems where the input is in trigonometric form and the output needs to be in angle measures, making them essential tools in many practical fields.

How do you solve equations involving inverse trigonometry functions?

To solve equations involving inverse trigonometry functions, first isolate the inverse trig function on one side of the equation. Then use the definition of the inverse trig function to find the angle that satisfies the equation. Keep in mind that there may be multiple solutions due to the periodic nature of trigonometric functions, so you may need to consider the domain over which the inverse function is defined. Lastly, be sure to check your solutions by substituting them back into the original equations to verify their validity.