Inverse Sin Cos Tan Worksheet
Are you on the lookout for a comprehensive and user-friendly worksheet that focuses on inverse sine, cosine, and tangent functions? Well, you're in luck! In this blog post, we will be introducing an excellent worksheet that is tailored for those who are studying trigonometry and need to practice their skills in determining the values of inverse trigonometric functions. With clear instructions and carefully-crafted questions, this worksheet will surely help you master the concept of inverse sin, cos, and tan.
Table of Images 👆
Sin Cos Tan
Find the Measure of Each Angle Worksheet
Inverse Trig Functions Worksheet
Special Angles of Trig Functions Worksheet
Trig Identity Cheat Sheet
Direct and Inverse Variation Worksheet Answer Key
Multiplication and Division Worksheets
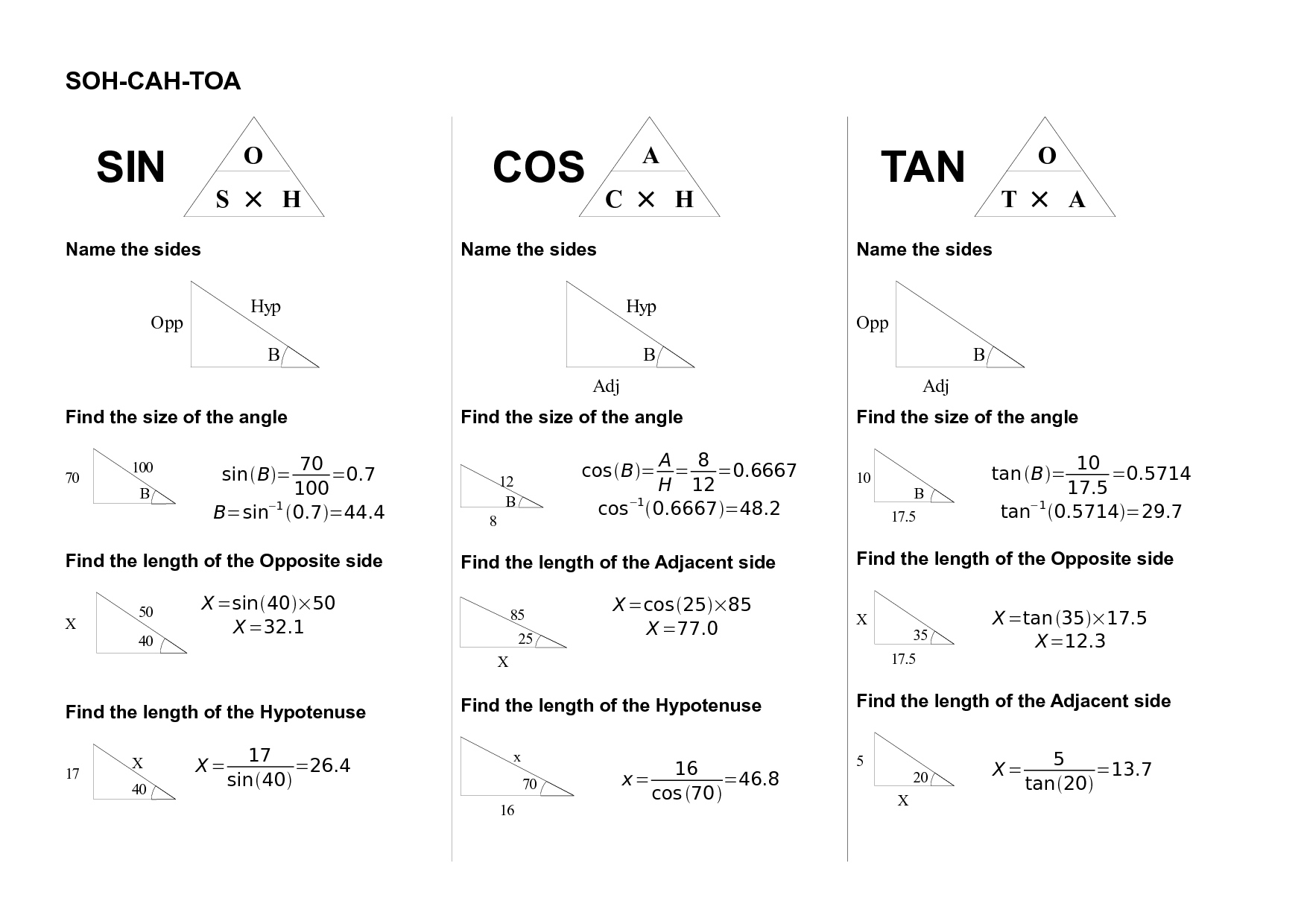
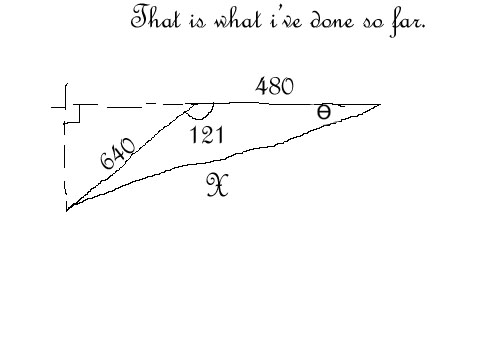
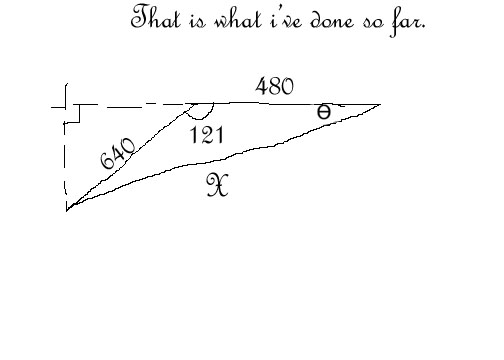
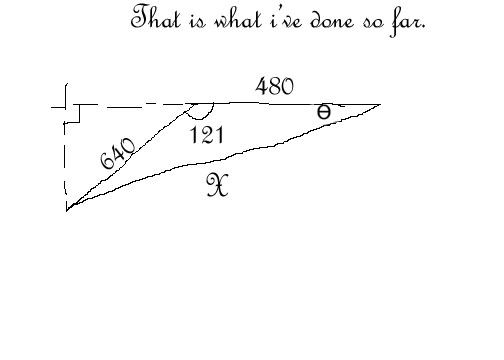
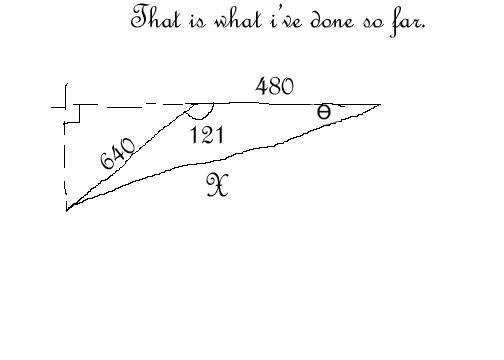
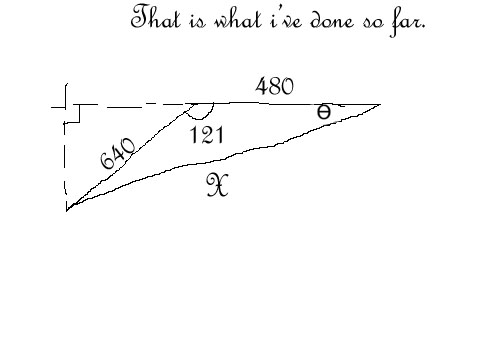
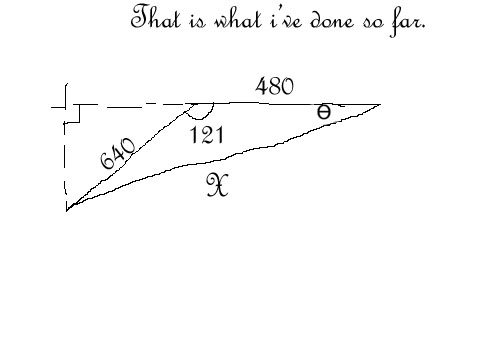
Bearing Distance Word Problems
Bearing Distance Word Problems
Bearing Distance Word Problems
Bearing Distance Word Problems
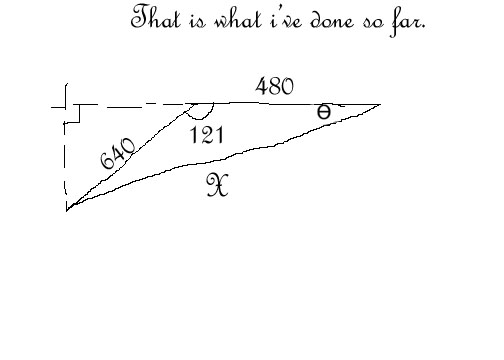
Bearing Distance Word Problems
Bearing Distance Word Problems
Bearing Distance Word Problems
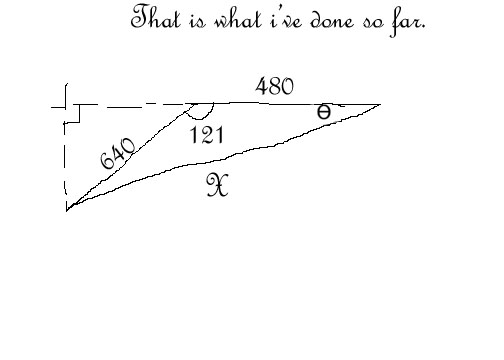
Bearing Distance Word Problems
Bearing Distance Word Problems
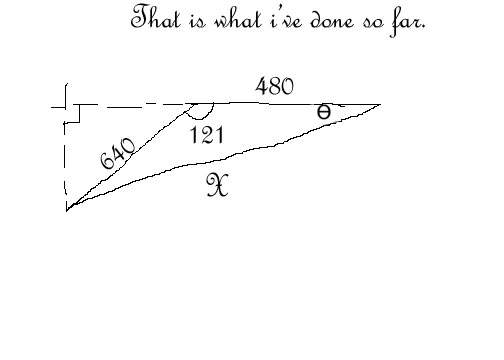
Bearing Distance Word Problems
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
All Amendment Worksheet
Symmetry Art Worksheets
Daily Meal Planning Worksheet
What are the values of inverse sin, cos, and tan functions?
The values of the inverse trigonometric functions sin^-1, cos^-1, and tan^-1 are typically within the range of -pi/2 to pi/2 for sin^-1, 0 to pi for cos^-1, and -pi/2 to pi/2 for tan^-1. These values correspond to the principal values or the main branches of the functions, and the exact values of the inverse trigonometric functions can be determined using trigonometric identities and geometric representations in the unit circle.
How are inverse sin, cos, and tan functions related to their respective trigonometric functions?
The inverse sine, cosine, and tangent functions are mathematical operations that undo the effects of the sine, cosine, and tangent functions based on the input values provided. They are related to their respective trigonometric functions as follows: the inverse sine function (sin^-1) takes a ratio value and outputs an angle measure whose sine is that ratio; the inverse cosine function (cos^-1) takes a ratio value and outputs an angle measure whose cosine is that ratio; and the inverse tangent function (tan^-1) takes a ratio value and outputs an angle measure whose tangent is that ratio. These inverse functions essentially "reverse" the process of the trigonometric functions to find the original angle measure.
What is the range of values for inverse sin, cos, and tan functions?
The range of values for the inverse sine (sin^-1) function is from -?/2 to ?/2, for the inverse cosine (cos^-1) function is from 0 to ?, and for the inverse tangent (tan^-1) function is from -?/2 to ?/2, excluding odd multiples of ?.
How do you evaluate inverse sin, cos, and tan functions using a calculator?
To evaluate inverse trigonometric functions (sin^(-1), cos^(-1), tan^(-1)) on a calculator, you would typically use the "shift" or "2nd" function key along with the trigonometric function key. For example, to calculate sin^(-1)(0.5), you would press the sin^(-1) or arcsin key (usually above the sin key) followed by inputting the value 0.5. Make sure your calculator is set to the appropriate mode (degrees or radians) based on the units given in the problem. Repeat the same process for cos^(-1) and tan^(-1) functions.
What is the principal value of an inverse trigonometric function?
The principal value of an inverse trigonometric function is the unique value within a specified range that is used to define the function. It is typically the value that falls within a specific interval that is chosen to make the inverse trigonometric function a single-valued function.
What is the significance of the unit circle when dealing with inverse sin, cos, and tan functions?
The unit circle is significant when dealing with inverse sin, cos, and tan functions because it provides a geometrical representation of these trigonometric functions. The inverse functions help us find the angle measurement that corresponds to a given trigonometric value, and the unit circle allows us to visualize these relationships in terms of the coordinates on the circle. By using the unit circle, we can determine the exact values of the inverse trigonometric functions and understand their connection to angles and triangles in a clear and intuitive way.
How do you find the domain and range of inverse sin, cos, and tan functions?
To find the domain and range of inverse trigonometric functions like sin^(-1), cos^(-1), and tan^(-1), you need to consider the restrictions imposed on the parent functions. The domain of sin^(-1) and cos^(-1) is -1 <= x <= 1, while the domain of tan^(-1) is all real numbers. The range of sin^(-1) and cos^(-1) is -?/2 <= y <= ?/2, whereas the range of tan^(-1) is -?/2 < y < ?/2. Keep in mind that the range of inverse trig functions can vary depending on the specific interval being considered.
What are the principal values of inverse sin, cos, and tan functions in degrees and radians?
The principal values of the inverse sine function (arcsin) range from -90° to 90° (-?/2 to ?/2 radians), the inverse cosine function (arccos) ranges from 0° to 180° (0 to ? radians), and the inverse tangent function (arctan) ranges from -90° to 90° (-?/2 to ?/2 radians). These principal values represent the primary output of the inverse trigonometric functions.
How are inverse trigonometric functions used to solve real-life problems?
Inverse trigonometric functions are used in real-life problems that involve finding angles in triangles or navigational problems, such as determining the angle of elevation for building structures, calculating the angle of a hill for road construction, or determining the angle necessary for launching a projectile. By using these functions, we can solve practical problems that require finding an angle when the ratio of sides is known, allowing for accurate measurements and calculations in various fields like engineering, physics, surveying, and astronomy.
Can you provide examples of evaluating inverse sin, cos, and tan for different angles?
Certainly! Evaluating the inverse sine, cosine, and tangent functions involves finding the angle in either degrees or radians that corresponds to a given value within the range of the functions. For example, the inverse sine of 0.5 is 30 degrees or ?/6 radians, the inverse cosine of -0.5 is 120 degrees or 2?/3 radians, and the inverse tangent of 1 is 45 degrees or ?/4 radians. These are just a few examples, and the values can vary depending on the input provided to the functions.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.
Comments