Geometry Reflection Worksheet
Are you searching for a resource to help your students practice geometric reflections? Look no further! We have created a geometry reflection worksheet that is perfect for students in middle and high school. This worksheet focuses on the concept of reflection and provides ample opportunities for students to explore and strengthen their understanding of this topic. With clear instructions and a variety of questions, this worksheet is designed to engage students and help them develop their skills in geometry.
Table of Images 👆
Reflection Math Worksheets
Reflection Worksheets
Reflections Over X and Y-Axis Worksheets
Geometry Slide Flip Turn Worksheets
Math Reflection Examples
Student Writing Reflection Sheet
Cube Volume Worksheets 5th Grade Math
Coordinate Plane Worksheets 6th Grade
Rotational Symmetry Worksheets
John Quincy Adams
John Quincy Adams
John Quincy Adams
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
All Amendment Worksheet
Symmetry Art Worksheets
Daily Meal Planning Worksheet
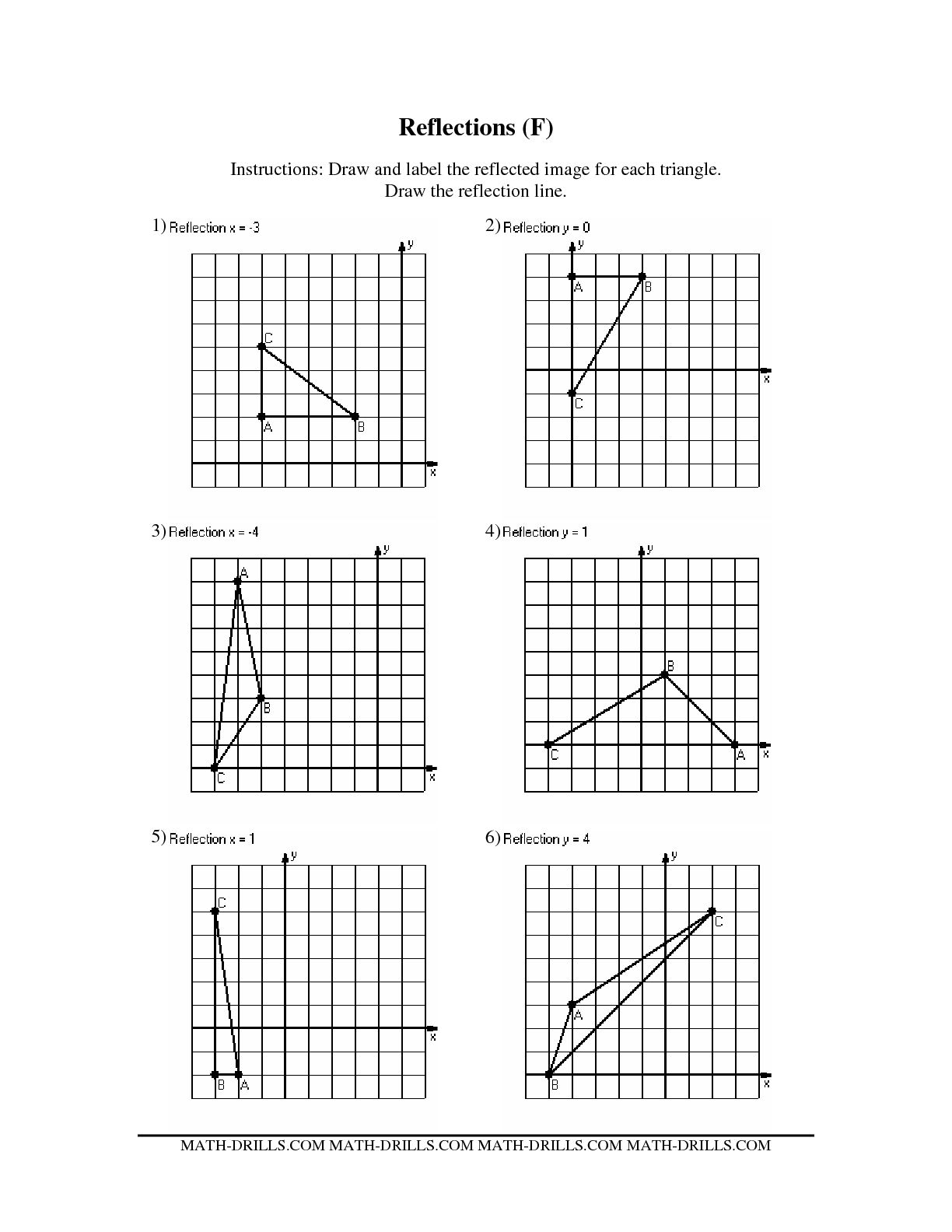
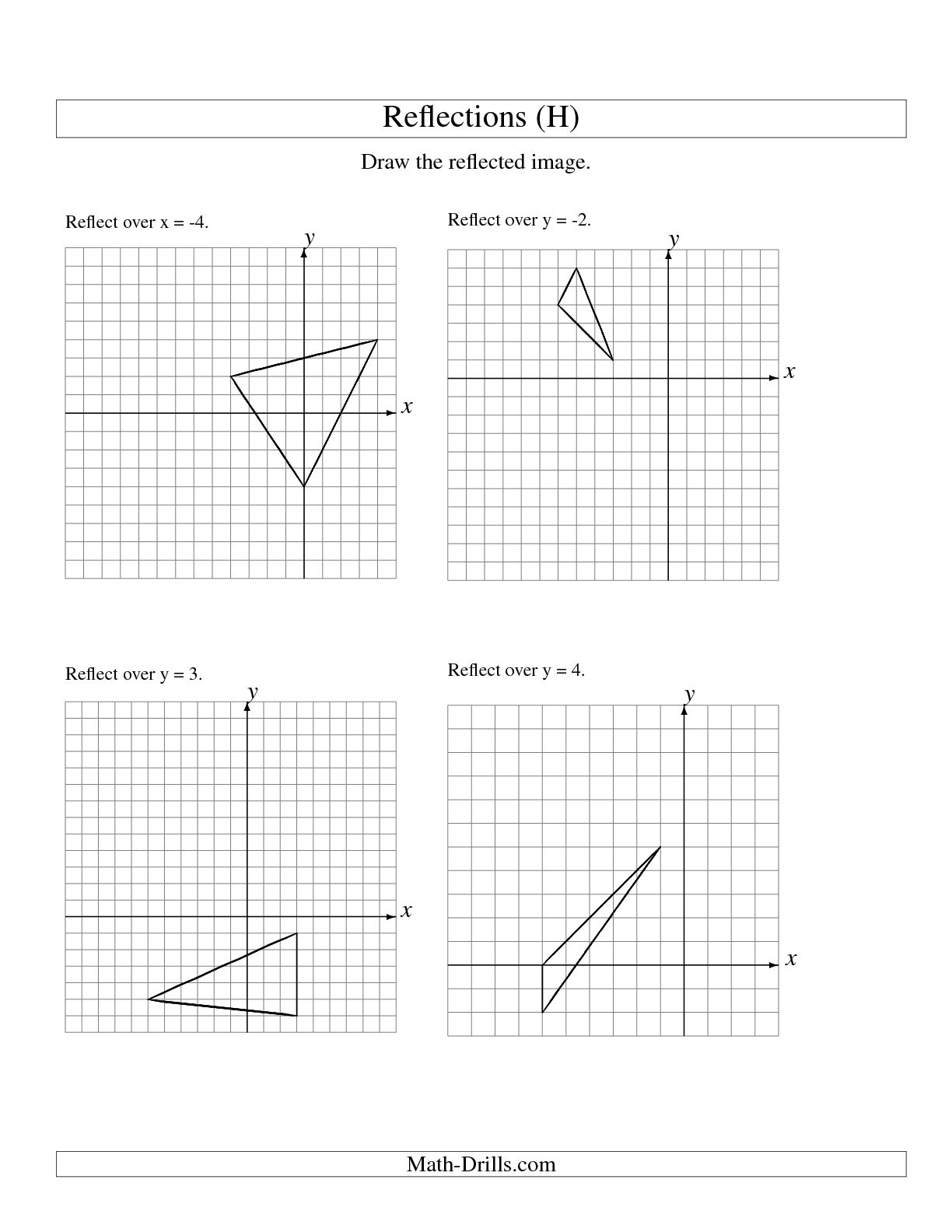
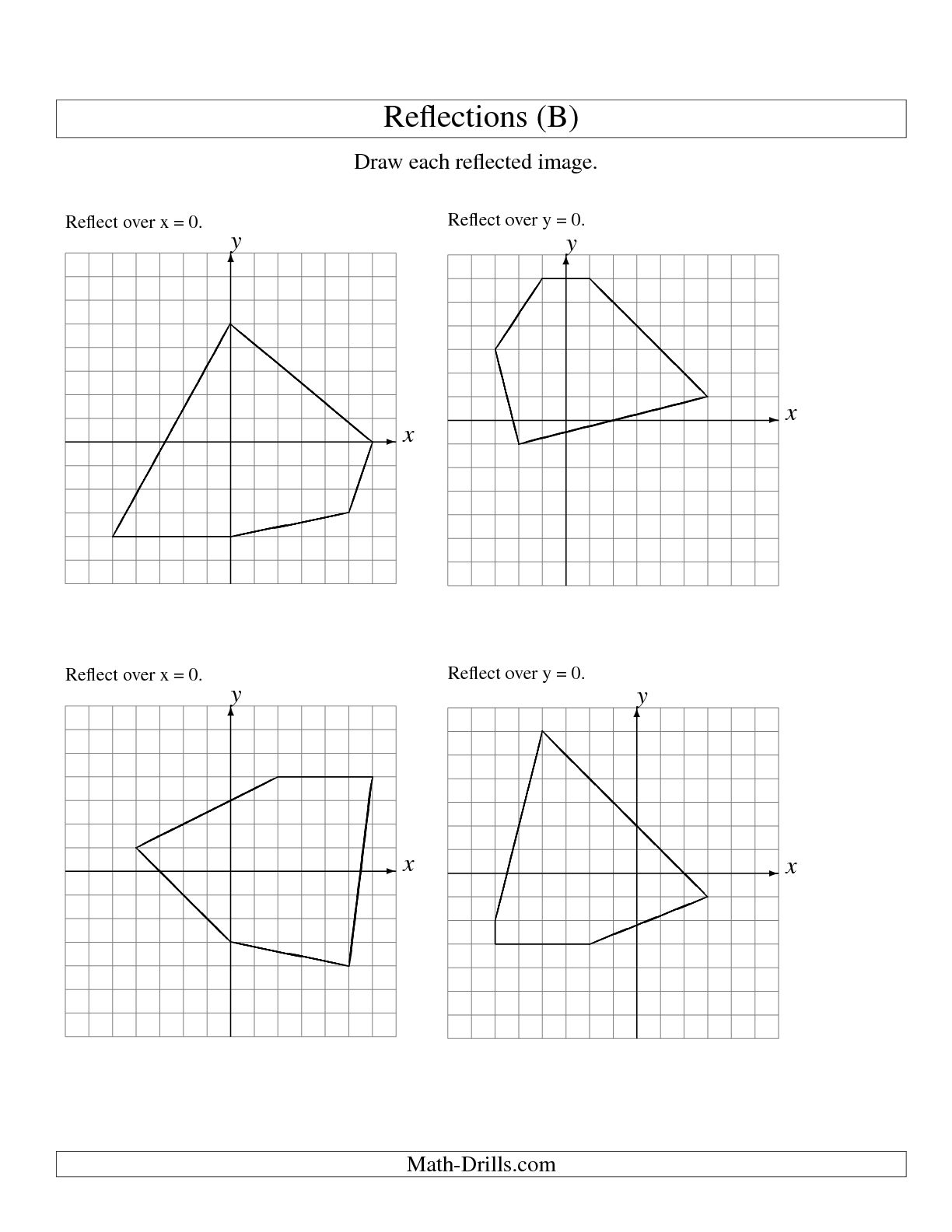
What is a reflection in geometry?
In geometry, a reflection is a transformation that flips a figure over a line, creating a mirror image. This line is called the axis of reflection, and every point on the original figure is the same distance from the axis as its reflected image. Reflection is a basic geometric operation that preserves angles and lengths, but reverses orientation.
How do you determine the axis of reflection?
To determine the axis of reflection, you need to find the perpendicular bisector of the line connecting each point on the pre-image to its corresponding point on the image. The axis of reflection is the line that lies equidistant between the pre-image and image points and is perpendicular to the line connecting them, serving as the mirror line for the reflection.
Define the term "line of symmetry" in relation to reflections.
A line of symmetry is a line that divides a shape or object into two equal halves, where each half is a mirror reflection of the other. When a shape is reflected across its line of symmetry, the two resulting halves overlap perfectly.
What is the relationship between the pre-image and image in a reflection?
In a reflection, the pre-image and image are related by a transformation that flips an object over a line called the line of reflection. The pre-image is the original shape or object, while the image is the result of applying the reflection transformation. The image is a mirror image of the pre-image across the line of reflection, maintaining the same shape but reversing the orientation.
Can a figure have more than one axis of reflection? Explain.
No, a figure cannot have more than one axis of reflection because a single axis of reflection is sufficient to reflect the entire figure across a line. Any additional axes of reflection would simply duplicate the reflection already achieved by the first axis, making them redundant. Therefore, a figure can only have one axis of reflection, which mirrors the shape across a specific line.
How can you use a reflection to determine congruence between two figures?
To determine congruence between two figures using a reflection, you would need to perform a reflection on one of the figures and then compare it to the other figure. If the reflected figure can be superimposed onto the other unchanged, then the two figures are congruent. This is because reflection preserves angles and side lengths, so if the two figures match up perfectly after a reflection, they are congruent.
What are the properties of a reflection in terms of angles and distances?
In a reflection, the angles between corresponding points of the original figure and its reflection are congruent, meaning they are equal in measure. Additionally, the distance between corresponding points of the original figure and its reflection is maintained, so the distance between any two corresponding points remains the same before and after the reflection.
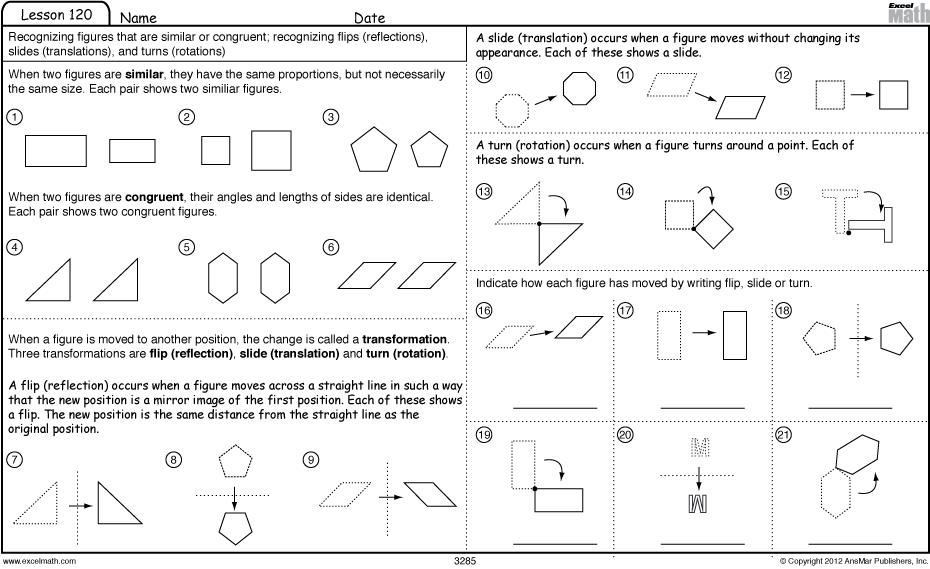
How is a reflection different from a translation or rotation?
A reflection is a transformation that flips an object over a line, creating a mirror image. In contrast, a translation is a transformation that moves an object from one location to another without changing its size or shape, while a rotation is a transformation that turns an object around a fixed point. Reflections involve flipping, translations involve shifting, and rotations involve turning.
Provide an example of a real-life application of reflection in geometry.
One real-life application of reflection in geometry is in architecture when designing buildings with mirrored facades. By using the concept of reflection, architects can create visually stunning structures that reflect their surroundings, manipulate natural light, and enhance the overall design aesthetic of the building.
Explain how a series of reflections can create a tessellation.
A tessellation is created by repeating a shape or design to cover a surface without any gaps or overlaps. When a series of reflections is applied to a shape, it can create a tessellation because each reflection copies and reflects the original shape to fit together seamlessly, forming a pattern that covers the entire space without leaving any gaps. By strategically arranging the reflections of the shape, a tessellating pattern is achieved, showcasing a balanced and repetitive design across the surface.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.
Comments