Geometric Lines Worksheets
Geometry is a fascinating subject that explores the different shapes and figures that make up our world. It provides a solid foundation for understanding the world around us. If you are a teacher or a parent looking for an effective way to reinforce geometric lines concepts, then you have come to the right place. In this blog post, we will discuss the benefits of using worksheets to engage students in meaningful learning experiences.
Table of Images 👆
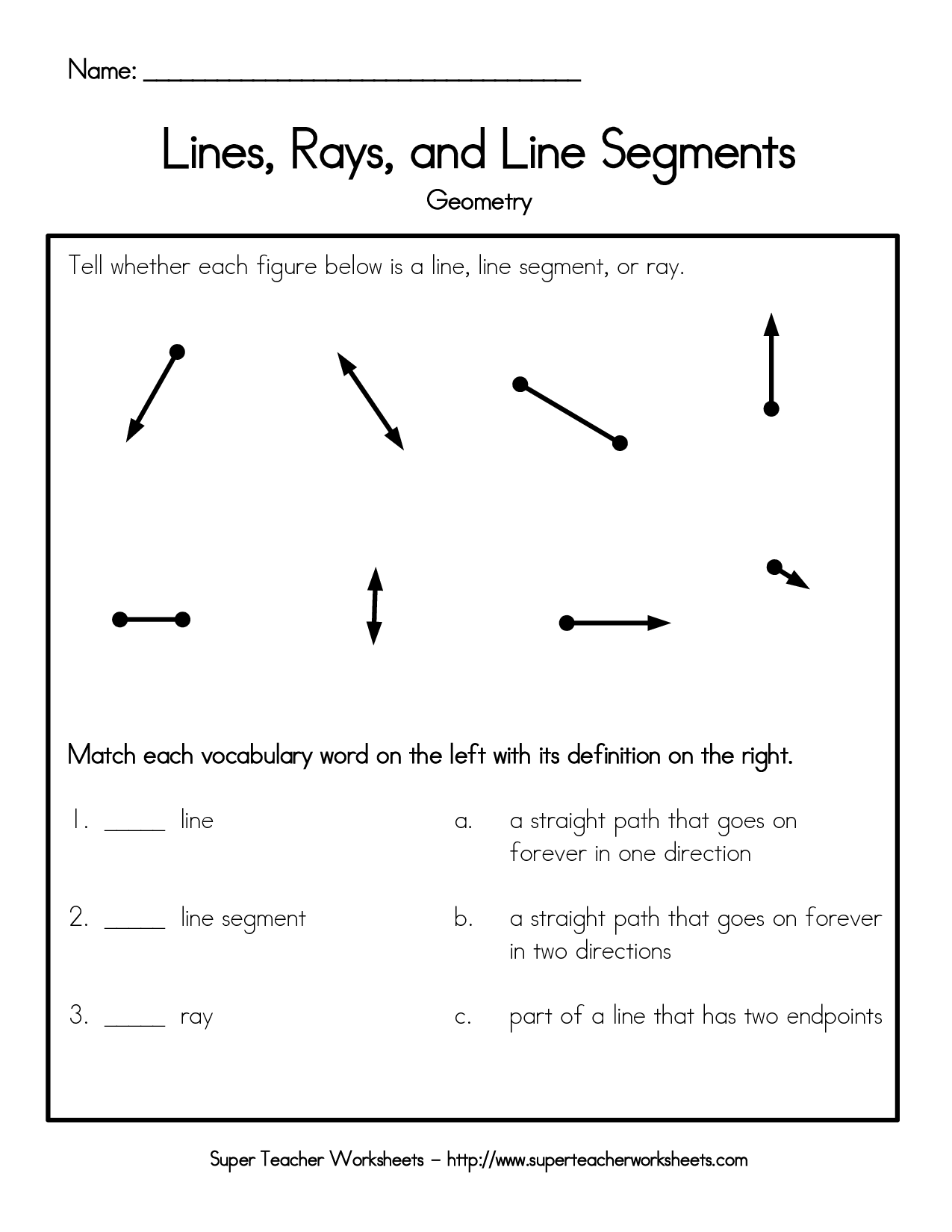
- Line Segments Rays Worksheets
- Circle Graph Worksheets 8th Grade
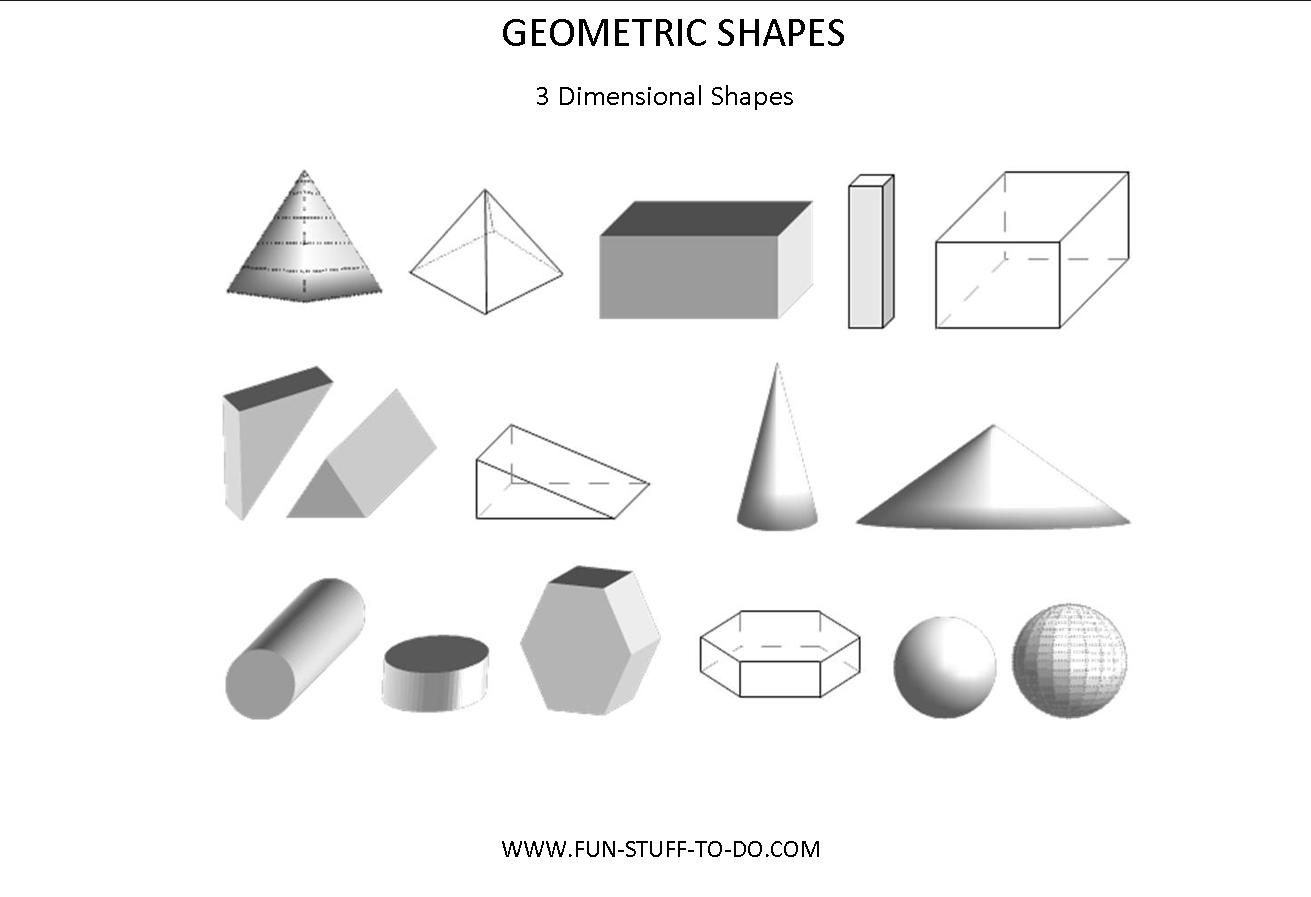
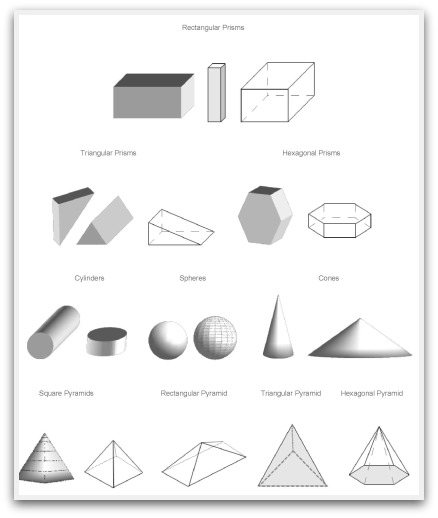
- Three-Dimensional Shapes Worksheets
- 3D Geometric Shapes
- Classifying Angles Geometry
- 8 X 10 Free Printable Adult Coloring Pages
- Tide Pool Worksheet
- Free Pre-K Shapes Worksheets
- Color Mandala Coloring Pages for Adults
- Clip Art Shapes with 7 Sides
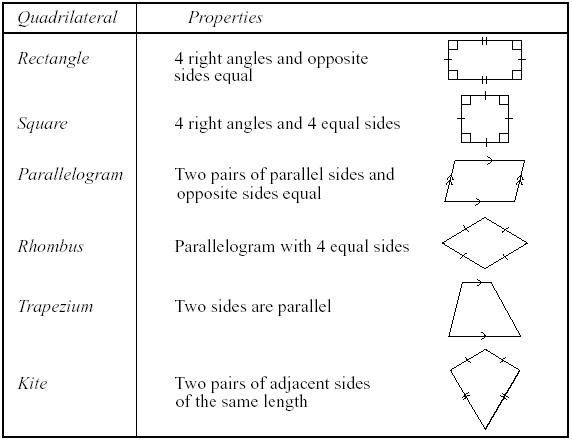
- Geometric Shapes and Properties
- Celtic Knot Border Patterns
- Geometry Vocabulary Reference Sheet Math
Line Segments Rays Worksheets
Circle Graph Worksheets 8th Grade
Three-Dimensional Shapes Worksheets
3D Geometric Shapes
Classifying Angles Geometry
8 X 10 Free Printable Adult Coloring Pages
Tide Pool Worksheet
Free Pre-K Shapes Worksheets
Color Mandala Coloring Pages for Adults
Clip Art Shapes with 7 Sides
Geometric Shapes and Properties
Celtic Knot Border Patterns
Geometry Vocabulary Reference Sheet Math
Geometry Vocabulary Reference Sheet Math
More Line Worksheets
Lines of Symmetry WorksheetsLine Drawing Art Worksheets
Drawing Contour Lines Worksheet
Blank Printable Timeline Worksheets
2 Lines of Symmetry Worksheets
Linear Equations Worksheet 7th Grade
Rounding Decimals Number Line Worksheet
College Essay Outline Worksheet
Texture Line Drawing Techniques Worksheet
Outline Format Worksheet
What is a geometric line?
A geometric line is an infinite set of points that extend in opposite directions without end. It has zero width and is perfectly straight, connecting any two points along its path. In geometry, a line is represented by a straight line segment with two arrowheads on both ends to symbolize its endless nature.
How is a line defined in geometry?
In geometry, a line is defined as a straight path that extends infinitely in both directions. It is composed of an infinite number of points that are collinear, meaning they lie on the same straight path. A line has no width or thickness, and it can be defined by just two points on it.
What are the characteristics of a straight line?
A straight line is defined by two main characteristics: it extends infinitely in both directions and all points on the line lie in a single direction. It has a constant slope, meaning the rate at which it rises or falls is the same throughout its length. Additionally, a straight line can be uniquely defined by two points on the line, allowing for precise determination and representation in geometry and mathematics.
Can a line have endpoints? Why or why not?
Yes, a line can have endpoints. A line is defined as a straight path that extends indefinitely in both directions, but if it is bounded or limited at both ends by distinct points, those points would be considered its endpoints.
How many points are needed to uniquely define a line?
Two points are needed to uniquely define a line. Given two distinct points, there is only one line that can pass through both points, making the line uniquely determined by those two points.
What is the difference between a line and a line segment?
A line is an infinite series of points that extends in opposite directions indefinitely, whereas a line segment is a portion of a line that has endpoints, making it finite in length.
How are parallel lines defined?
Parallel lines are defined as two lines in a plane that never meet each other, meaning they do not intersect at any point. When extended infinitely in both directions, parallel lines will always maintain the same distance between them.
How are perpendicular lines defined?
Perpendicular lines are defined as lines that intersect at a 90-degree angle, forming a right angle where they meet. In other words, if two lines are perpendicular, they can be pictured as two straight lines that cross each other in such a way that the angles formed at the point of intersection are equal to 90 degrees.
Can two lines intersect at more than one point? Explain.
Two lines can only intersect at one point if they lie in the same plane. If the lines are in different planes, they may appear to intersect at multiple points, but in reality, they are not truly intersecting. This is because each plane extends infinitesimally in all directions, creating the appearance of multiple intersection points when viewed from a specific perspective. However, mathematically speaking, two lines can only intersect at one point in a flat or two-dimensional space.
How can the slope of a line be determined?
The slope of a line can be determined by taking the ratio of the change in the y-coordinates to the change in the x-coordinates between any two points on the line. This ratio, known as rise over run, provides the slope of the line and indicates how steep the line is. Mathematically, the slope of a line can be calculated using the formula (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of two points on the line.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.
Comments