Factoring Quadratics Worksheet

Factoring quadratics can be a challenging concept for students to grasp. It requires a solid understanding of both algebraic expressions and factoring techniques. If you're a math teacher or a student looking to practice and strengthen your skills in this area, you might find worksheets to be a helpful tool. Worksheets provide a structured and systematic approach to practising factoring quadratics, allowing you to work through various problems at your own pace. By focusing on the entity and subject of factoring quadratics, these worksheets are designed to assist learners in honing their factoring skills and reinforcing their knowledge of quadratic equations.

  Solving Quadratic Equations by Factoring Worksheet

---

  Factoring Quadratic Expressions

---

  Algebra 1 Factoring Worksheets with Answers

---

  Factoring Quadratic Expressions Worksheet

---

  Factoring Quadratic Expressions Worksheet

---

  Factoring Quadratic Expressions Worksheet

---

  Solving Quadratic Equations in Factored Form

---

  Solving Quadratics Worksheet

---

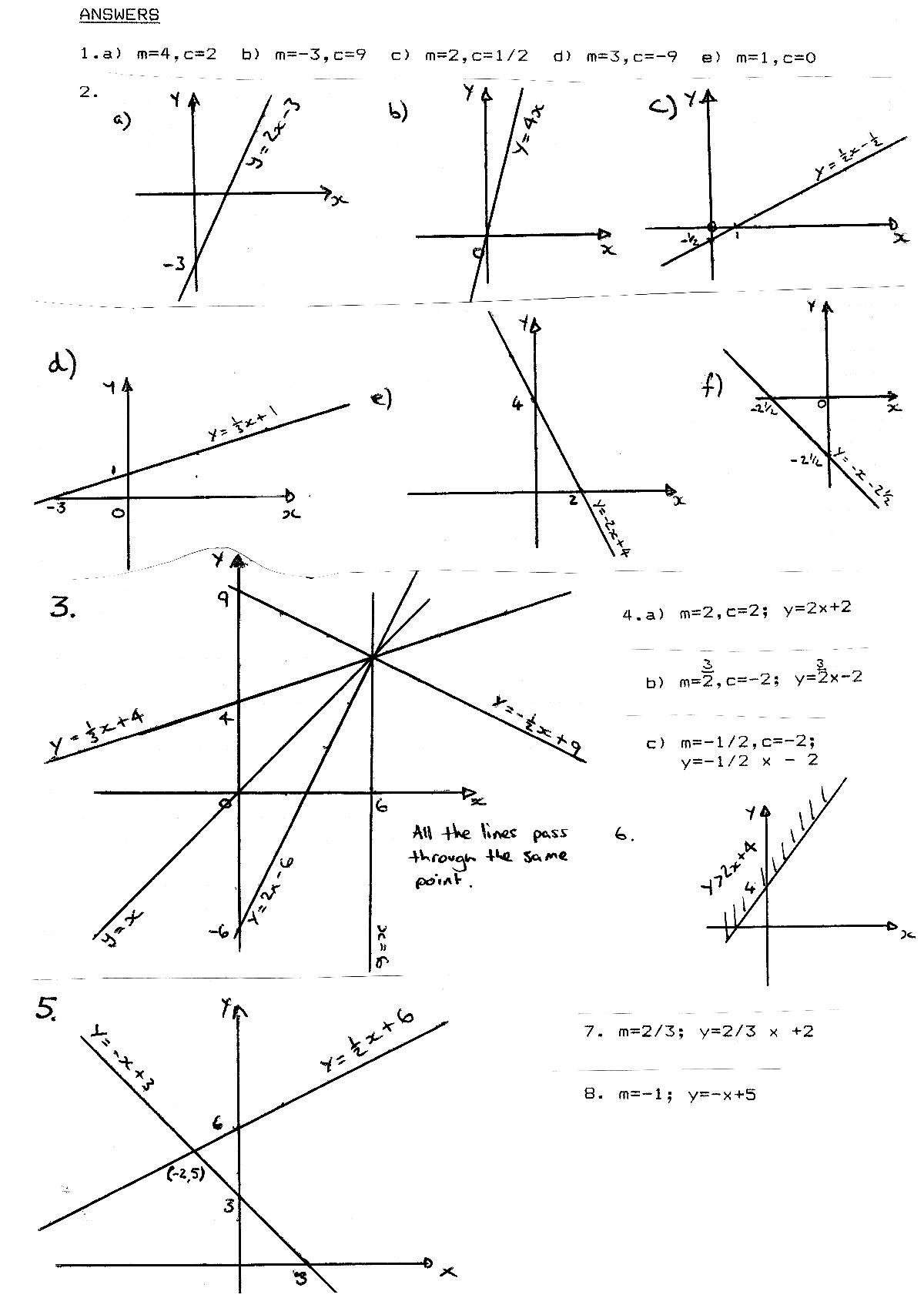
  Algebra 1 Worksheets

---

  Linear Equations Worksheets

---

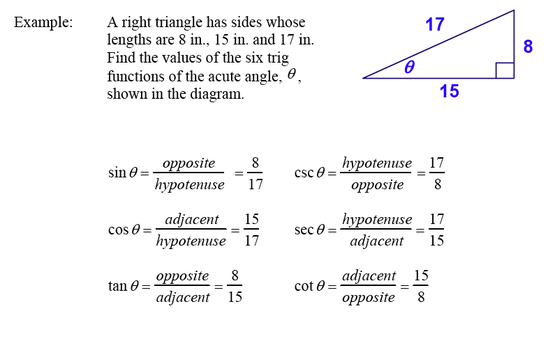
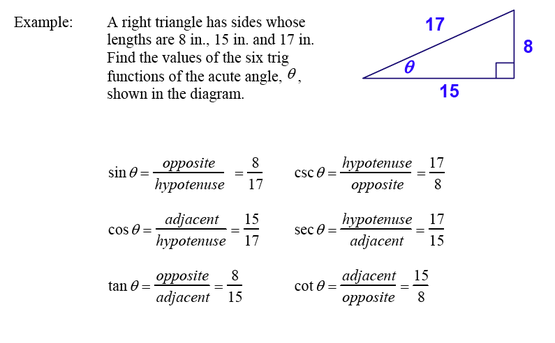
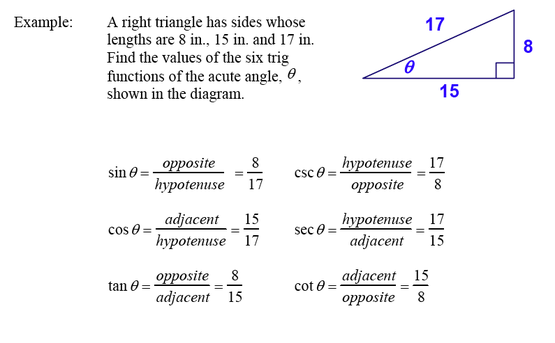
  Right Triangle Trigonometry

---

  Right Triangle Trigonometry

---

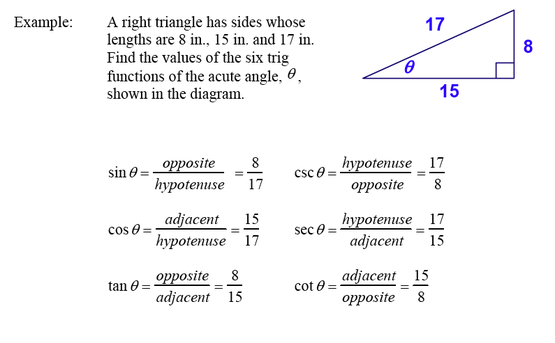
  Right Triangle Trigonometry

---

  Right Triangle Trigonometry

---

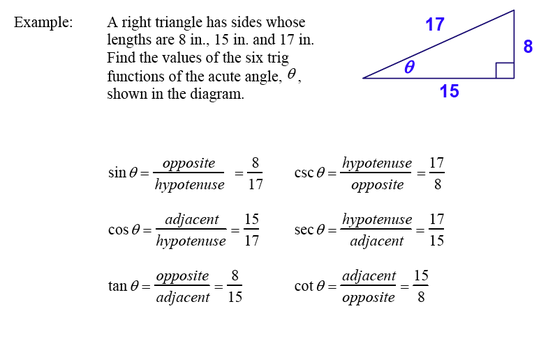
  Right Triangle Trigonometry

---

What is factoring in the context of quadratic expressions?

Factoring in the context of quadratic expressions refers to the process of expressing a quadratic expression as the product of two binomial expressions. It involves finding two binomial factors that, when multiplied together, equal the original quadratic expression. Factoring quadratic expressions is a crucial skill in algebra as it helps simplify and solve equations and expressions involving quadratic terms.

How can factoring be used to solve quadratic equations?

Factoring can be used to solve quadratic equations by rewriting a quadratic equation in the form of (x - a)(x - b) = 0, where a and b are the solutions to the equation. By factoring the quadratic equation and setting each factor to zero, the solutions can be found by solving for x. Factoring can help simplify the process of solving quadratic equations and identify the roots of the equation efficiently.

What are the steps involved in factoring a quadratic expression?

To factor a quadratic expression, first set the expression equal to zero. Then factor out any common terms or use the quadratic formula to find the roots. Once the roots are known, write the expression as a product of factors with the roots as the solutions. Remember to simplify the expression by combining like terms, if necessary.

How can you determine if a quadratic expression is factorable or not?

A quadratic expression is factorable if it can be rewritten as the product of two binomial expressions. To determine if a quadratic expression is factorable, you can use the quadratic formula or factorization techniques such as factoring by grouping or the AC method. If the quadratic expression can be factored into two binomial expressions where the constant term and leading coefficient are integers, then it is factorable. If the quadratic cannot be factored in this way, it is not factorable over the integers.

What is the significance of factoring quadratics in real-world applications?

Factoring quadratics is significant in real-world applications because it helps in solving problems related to areas such as finance, engineering, science, and statistics. By breaking down quadratic equations into simpler forms, we can analyze and understand the behavior of these systems, make predictions, optimize processes, and make informed decisions. Factoring quadratics can also help in determining the roots of a function, finding maximum or minimum values, and identifying patterns or relationships present in various data sets. Overall, factoring quadratics plays a crucial role in problem-solving and critical thinking across different disciplines.

How does factoring help in finding the x-intercepts or roots of a quadratic function?

Factoring a quadratic function helps in finding the x-intercepts or roots by breaking down the function into two linear expressions set equal to zero. By setting each factor to zero and solving for the variable, you can find the x-values where the function crosses the x-axis, which represent the x-intercepts or roots of the quadratic function. This method simplifies the process of solving for the roots of a quadratic function compared to other methods such as the quadratic formula, making it a useful technique in algebraic calculations.

Can all quadratic expressions be factored? Why or why not?

Not all quadratic expressions can be factored. This is because some quadratic expressions, such as those with complex roots, may not have real solutions that can be factored using integers. Additionally, some quadratic expressions may be prime and cannot be factored into simpler polynomials. Overall, the factorability of a quadratic expression depends on its specific coefficients and roots.

What are the common factoring techniques used for quadratics, such as difference of squares or grouping?

Common factoring techniques used for quadratics include difference of squares, which involves factoring expressions in the form of \(a^2 - b^2\), and grouping, where terms in a quadratic expression are grouped together and factored by finding common factors or using other factoring techniques like the AC method to simplify the expression. Other techniques include factoring by trial and error, factoring trinomials, and factoring by completing the square or using the quadratic formula for more complex expressions.

How can factoring help in simplifying or manipulating quadratic expressions?

Factoring can help simplify quadratic expressions by breaking them down into product of factors, making it easier to work with and manipulate. By factoring a quadratic expression, you can identify common terms, find the roots or solutions, and ultimately solve equations efficiently. Factoring also allows you to easily graph the quadratic equation, determine whether it can be further simplified, or be used to identify patterns and relationships within the expression.

What are the limitations or challenges in factoring quadratics?

There are several limitations and challenges when factoring quadratics, such as the possibility of complex roots, the need for trial and error when factoring with large coefficients, and the difficulty in factoring quadratics that do not have rational roots. Additionally, factoring can be time-consuming and require a good understanding of algebraic concepts and techniques. Some quadratics may also require advanced methods like completing the square or using the quadratic formula if they cannot be easily factored using traditional methods.