Factoring Expressions Worksheet 7th Grade
Are you searching for a helpful resource to enhance your 7th-grade math skills? Look no further! We have created a factoring expressions worksheet that is tailored to provide a comprehensive understanding of this essential topic. Whether you are a student looking to ace your math exams or a parent seeking additional practice materials, this worksheet is designed to assist you in mastering the art of factoring expressions.
Table of Images 👆
- Algebra Factoring Polynomials Worksheet
- 5th Grade Algebra Variables Worksheets
- Math Expressions Worksheets 7th Grade
- 7th Grade Math Problems Worksheets
- Distributive Property Worksheets 7th Grade
- 7th Grade Math Algebra Equations Worksheets
- Math Expressions Worksheets 7th Grade
- Scale Factor Worksheets 7th Grade
- 7th Grade Math Scale Factor Worksheets
- Factoring Polynomials Practice Worksheet
- 7th Grade Math Test Worksheets
- 7th Grade Math Problems Worksheets
- 7th Grade Math Worksheets
- Algebraic Expressions Worksheets 6th Grade
- 7th Grade Math Scale Factor Worksheets
- 7th Grade Math Scale Factor Worksheets
More 7th Grade Worksheets
7th Grade Math Worksheets with Answer Key7th Grade Vocabulary Worksheets
Pre-Algebra 7th Grade Math Worksheets
Reading Comprehension Worksheets 7th Grade
7th Grade Math Worksheets Proportions
Complex Sentence Worksheets 7th Grade
Geometry Angles Worksheet 7th Grade Math
What is factoring?
Factoring is the process of breaking down a mathematical expression into simpler terms, typically involving finding the prime factors of a number or identifying common factors in algebraic expressions. This technique is commonly used in mathematics to simplify calculations, solve equations, and identify patterns or relationships between numbers or variables.
How is factoring different from simplifying?
Factoring involves breaking down a mathematical expression into its individual components, usually in terms of multiplication. Simplifying, on the other hand, focuses on reducing an expression to its most compact or concise form by combining like terms, grouping similar factors, or applying mathematical rules to streamline the expression. In essence, factoring is more about breaking down an expression, while simplifying is about condensing it.
Why do we factor expressions?
Factoring expressions is important because it helps simplify and solve mathematical equations. By breaking down an expression into smaller factors, we can more easily identify common factors, find solutions, and understand the behavior of the expression. Factoring also allows us to explore relationships between numbers and variables, which can be useful in various areas of mathematics, such as algebra and calculus.
What are the steps to factor a quadratic expression?
To factor a quadratic expression, first check if the expression is in the form ax^2 + bx + c, then find two numbers that multiply to ac (the product of a and c in the expression) and add up to b. Use these numbers to rewrite the middle term of the expression. Finally, factor the expression using these new terms, typically resulting in a binomial expression. Make sure to simplify and check by multiplying the factors back to the original quadratic expression to confirm correctness.
What is the difference between factoring a quadratic expression and factoring a trinomial expression?
Factoring a quadratic expression involves factoring an expression with two terms, typically in the form of \( ax^2 + bx \) or \( x^2 + c \), where either \( a \) or \( b \) can be zero. On the other hand, factoring a trinomial expression involves factoring an expression with three terms, typically in the form of \( ax^2 + bx + c \), where \( a \) is not equal to zero. Factoring quadratic expressions can lead to one or two binomial factors, while factoring trinomial expressions usually requires the use of methods like the grouping method or trial and error to find the binomial factors.
What is the greatest common factor (GCF) and how is it used in factoring?
The greatest common factor (GCF) is the largest number that divides evenly into a set of numbers. In factoring, the GCF is essential for simplifying expressions by finding the common factor shared by all terms in an expression. By dividing each term by the GCF, you can reduce the expression to its simplest form, making it easier to work with and solve further. Identifying the GCF allows for efficient factoring and helps in finding the prime factorization of a number.
How can factoring be used to solve equations?
Factoring can be used to solve equations by breaking down a polynomial equation into simpler factors, which can help identify the roots or solutions to the equation. By factoring an equation, it becomes easier to manipulate and solve for the variable by setting each factor equal to zero. This technique is especially useful for quadratic equations, where factoring can help find the roots quickly and efficiently.
Can all expressions be factored? Why or why not?
Not all expressions can be factored. Some expressions contain terms that cannot be further simplified or factored, such as prime numbers or variables raised to prime exponents. Additionally, some expressions may have factors that do not simplify nicely or have complex roots, making factoring difficult or impossible using standard techniques. In such cases, the expression is said to be "irreducible" or "prime.
What are some common factoring patterns?
Some common factoring patterns include the difference of squares, perfect square trinomials, grouping, and factoring by common factors. The difference of squares pattern involves factoring a binomial in the form of (a^2 - b^2) into (a + b)(a - b). Perfect square trinomials involve factoring a trinomial in the form of (a^2 + 2ab + b^2) or (a^2 - 2ab + b^2) into (a + b)^2 or (a - b)^2. Grouping involves grouping terms in a polynomial and factoring out common factors. Lastly, factoring by common factors involves factoring out the greatest common factor of all terms in a polynomial.
Can factoring expressions be applied to real-life situations?
Yes, factoring expressions can be applied to real-life situations, such as determining the cost of making multiple copies of a blueprint or calculating the amount of material needed for a construction project. Factoring allows for simplifying complex equations or expressions, which can help in making decisions, managing resources efficiently, and solving practical problems in various fields such as finance, engineering, and science.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.

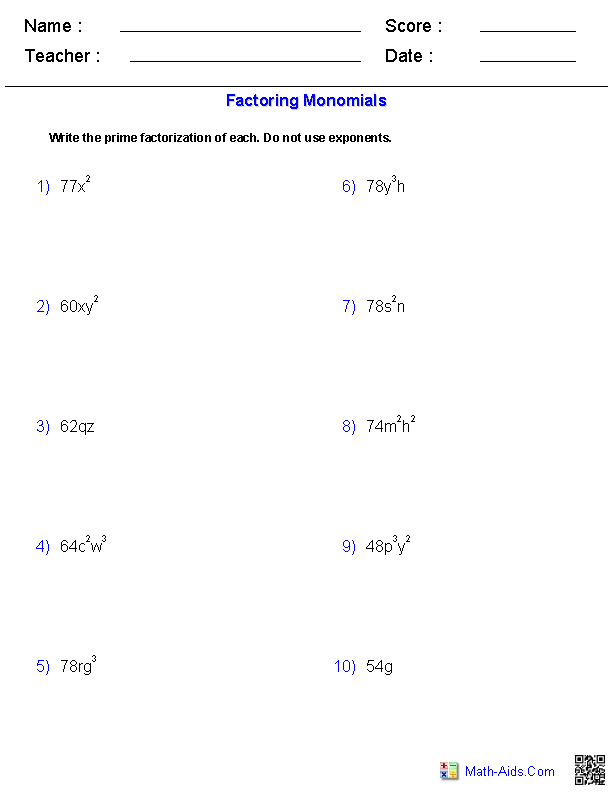



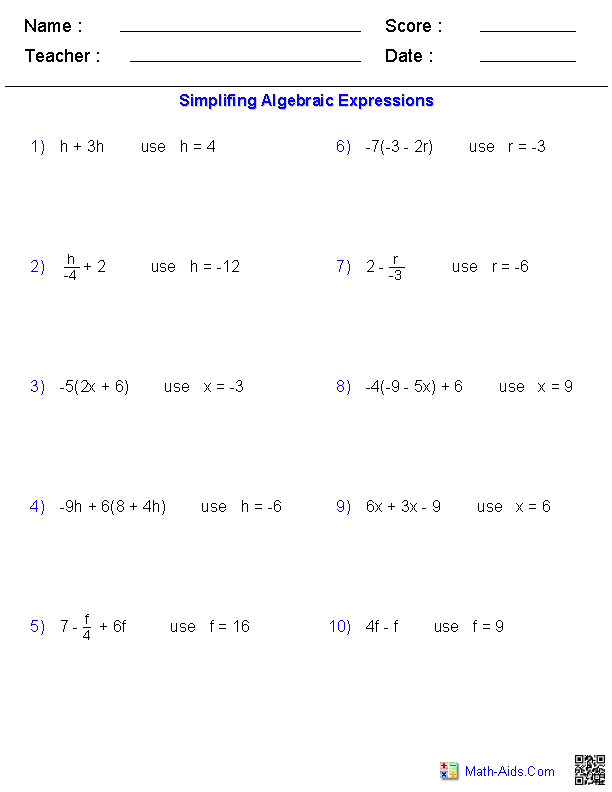



























Comments