Exponential Equations Worksheet

Are you a high school or college student studying algebra and struggling with solving exponential equations? If so, you're not alone. Many students find this topic challenging and are often looking for extra practice to strengthen their skills. Look no further, because we have the perfect solution for you - an exponential equations worksheet that will help solidify your understanding of this important concept.

  Bacteria Exponential Growth Worksheet

---

  8th Grade Math Worksheets Algebra

---

  Order of Operations Worksheets 6th Grade

---

  12th Grade Pre Calculus Problems

---

  Two-Step Equation Maze Answer Key Worksheet

---

  Exponents Worksheets

---

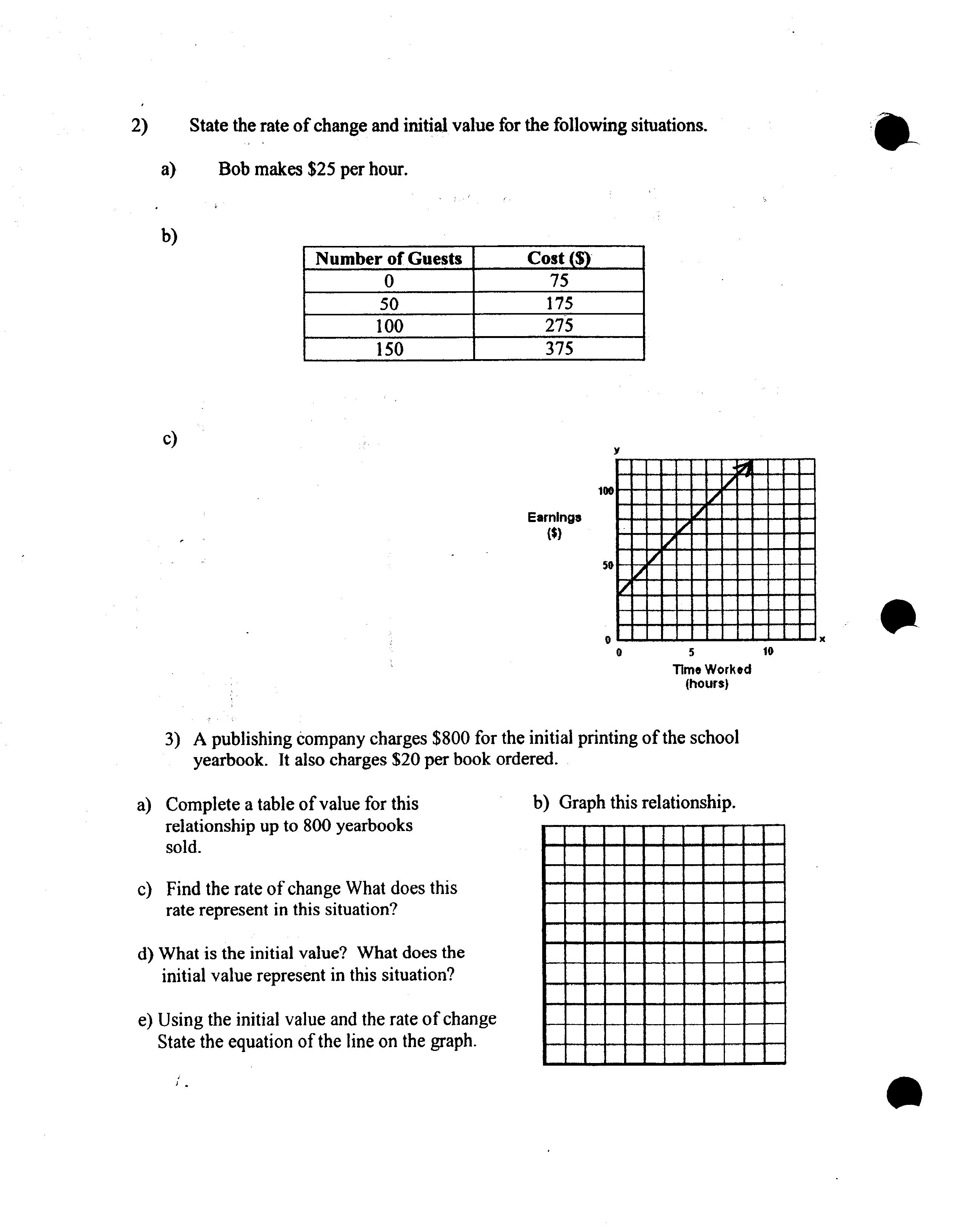
  Linear Relationships Worksheet

---

  Standard Form Place Value Worksheets

---

  Graphing Linear Inequalities Worksheet

---

  Order of Operations Worksheets 6th Grade

---

  Adding Fractions Worksheets 5th Grade Math

---

  Adding Fractions Worksheets 5th Grade Math

---

What is an exponential equation?

An exponential equation is a mathematical expression in which a variable appears in the exponent. Exponential equations typically involve a base raised to a power that is a variable, often denoted as y = a^x, where a is the base, x is the exponent, and y is the result. These equations are commonly used in modeling exponential growth or decay phenomena and can be solved using logarithms or by manipulating the equation algebraically.

How do you solve an exponential equation with the same base on both sides?

To solve an exponential equation with the same base on both sides, you can use the property that if bases are equal, the exponents must be equal as well. Simply set the exponents on both sides equal to each other and solve for the variable. For example, if you have an equation like \(3^x = 3^5\), you would set \(x = 5\) as the solution.

How do you solve an exponential equation with different bases on both sides?

To solve an exponential equation with different bases on both sides, you can use logarithms. Take the logarithm of both sides with the same base, which will help you convert the exponential equation into a simpler form that can be solved algebraically. Then, solve for the variable by isolating it on one side of the equation. Remember to check for extraneous solutions and make sure that the final solution satisfies all necessary conditions.

What is the difference between exponential growth and exponential decay?

Exponential growth refers to a situation where a quantity increases at a constant percentage rate over equal intervals of time, resulting in rapid and continuous growth. On the other hand, exponential decay occurs when a quantity decreases at a constant percentage rate over equal intervals of time, leading to a steady decline in value. Both processes follow exponential functions, but growth leads to a rapid increase, whereas decay involves a continuous decrease in quantity.

How do you solve exponential equations using logarithms?

To solve exponential equations using logarithms, you can take the natural logarithm (ln) or common logarithm (log base 10) of both sides of the equation to eliminate the exponential part. Then you can use the properties of logarithms to simplify the equation and isolate the variable. Finally, solve for the variable by applying the inverse operation of the logarithm used. Remember to check for extraneous solutions that may not satisfy the original exponential equation.

What is the natural base in exponential equations?

The natural base in exponential equations is denoted as "e" and has a numerical value of approximately 2.71828. It is a significant constant in mathematics and often arises in exponential growth and decay problems, as well as in calculus and advanced mathematical concepts.

How do you graph exponential equations?

To graph exponential equations, plot a few points by choosing values for x and calculating the corresponding y values using the equation. Exponential functions either increase or decrease rapidly, so choose x values that spread out horizontally to capture the steep trend. Connect the points smoothly to show the curve of the exponential function. Remember that exponential functions typically have a horizontal asymptote on one side of the graph, showing that the function either approaches or moves away from the line but does not touch it.

How can you determine if an exponential equation has no solution?

An exponential equation has no solution if the base of the exponential term is positive and not equal to 1, and the exponent results in a negative number. This is because any real number raised to a negative exponent will be a fraction, and a positive base raised to a negative exponent will never be equal to 0. Therefore, if you encounter such a situation when solving an exponential equation, it means that there is no solution for that equation.

What are some real-life applications of exponential equations?

Real-life applications of exponential equations include population growth models, compound interest calculations, radioactive decay in nuclear physics, modeling the spread of diseases, predicting the growth of bacterial cultures, analyzing the growth of social media users, and forecasting the depreciation of assets over time. These exponential equations are used in various fields such as biology, finance, physics, and social sciences to make predictions and informed decisions based on exponential trends and patterns.

How can you check if a solution to an exponential equation is correct?

To check if a solution to an exponential equation is correct, you can simply substitute the solution back into the original equation and see if it satisfies the equation. If the solution makes both sides of the equation equal, then it is correct. However, if it doesn't, then the solution is incorrect.