Exponential and Logarithmic Equations Worksheet
Are you a high school or college student studying exponential and logarithmic equations? If so, you may find this exponential and logarithmic equations worksheet extremely helpful. This comprehensive worksheet is designed to provide you with ample practice on solving equations involving exponential and logarithmic functions.
Table of Images 👆
- Exponential Functions and Equations Worksheet
- Exponential and Logarithmic Functions Worksheet
- Properties of Logarithms Algebra 2 Worksheet Answers
- Properties of Logarithms Algebra 2 Worksheet Answers
- Exponential Logarithmic Equations Worksheet
- Logarithmic to Exponential Form Worksheet
- Logarithmic to Exponential Form Worksheet
- Solving Exponential Equations Algebra
- Change of Base Formula Worksheet
- Exponential and Logarithmic Functions Worksheet
- Solving Exponential and Logarithmic Equations Worksheet
- Exponential Function Worksheets and Answers
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is the general form of an exponential equation?
The general form of an exponential equation is \( y = a \cdot b^x \), where \( a \) is the initial value or starting point when \( x = 0 \), \( b \) is the base of the exponential function, and \( x \) is the variable representing the exponent.
How do you solve an exponential equation using logarithms?
To solve an exponential equation using logarithms, first take the logarithm of both sides of the equation. Then use properties of logarithms to simplify and isolate the variable. Once the variable is isolated, solve for it by either exponentiating or using the properties of logarithms. Be mindful of any restrictions on the domain of the logarithmic function used in the process.
What is the definition of a logarithm?
A logarithm is the exponent to which a specific base must be raised to obtain a given number. In simpler terms, it is the inverse operation of exponentiation.
How do you write an exponential equation in logarithmic form?
To write an exponential equation in logarithmic form, you can use the following format: If \(a^{b} = c\), then \(\log_{a}(c) = b\), where 'a' is the base, 'b' is the exponent, and 'c' is the result of the exponential equation. By converting the exponential equation to logarithmic form, you can find the exponent when the base and result are known.
What is the basic property of logarithms used to solve logarithmic equations?
The basic property of logarithms used to solve logarithmic equations is the logarithmic property of inverses, which states that taking the logarithm of a number allows one to find the exponent to which a specific base must be raised to obtain that number. This property is key in simplifying and solving logarithmic equations by allowing us to convert logarithmic expressions into exponential form for easier manipulation and calculation.
How do you solve a logarithmic equation?
To solve a logarithmic equation, isolate the logarithm on one side of the equation, then rewrite the equation in exponential form. Next, solve for the variable using properties of exponents. Remember to check for extraneous solutions that may not be valid in the original logarithmic equation.
What is the difference between a natural logarithm and a common logarithm?
The difference between a natural logarithm and a common logarithm lies in the base they are based on. A natural logarithm, denoted as ln(x), is a logarithm with base 'e' (Euler's number, approximately equal to 2.718). On the other hand, a common logarithm, denoted as log(x) or log10(x), is a logarithm with base 10. This means that the natural logarithm calculates the exponent needed to equal 'e' to the power of that number, while the common logarithm calculates the exponent needed to equal 10 to the power of that number.
How do you solve an exponential equation when both sides have bases that can't be easily equalized?
To solve an exponential equation with bases that can't be easily equalized, you can use logarithms. Take the logarithm of both sides of the equation using a base that allows you to easily transform the equation into a form where you can isolate the variable. Once you have the equation in a log form, you can solve for the variable using algebraic techniques.
What are the properties of logarithms used for simplifying logarithmic expressions?
Logarithms have several properties that can be used to simplify logarithmic expressions, including the product property (log(a) + log(b) = log(ab)), the quotient property (log(a) - log(b) = log(a/b)), the power property (n * log(a) = log(a^n)), and the change of base formula (log_b(a) = log_c(a) / log_c(b)). These properties can help manipulate logarithmic expressions to make them easier to compute or compare.
How do you solve a logarithmic equation with a variable both inside and outside the logarithm?
To solve a logarithmic equation with a variable both inside and outside the logarithm, you first need to isolate the logarithmic expression by moving all other terms to the other side of the equation. Then apply the properties of logarithms to simplify the equation. Afterward, convert the logarithmic form to exponential form and solve for the variable. Remember to check your solutions to ensure they are valid for the original equation.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.






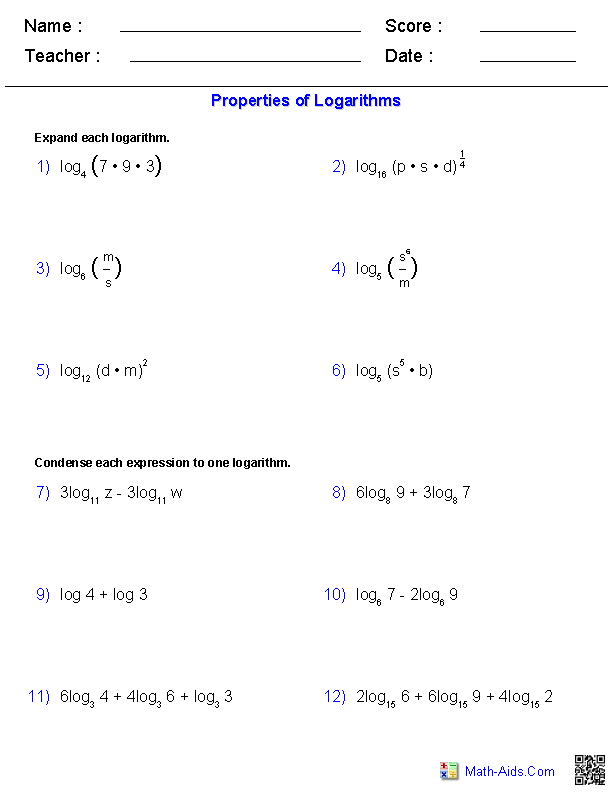























Comments