Exponent Rules Worksheet
Are you struggling with understanding the rules of exponents? Look no further, as we have the perfect solution for you. Our exponent rules worksheet is designed to help students grasp the concept of exponents and apply the appropriate rules in various mathematical problems. Whether you are a middle schooler, high schooler, or even an adult looking to refresh your math skills, this worksheet is suitable for anyone wanting to strengthen their understanding of exponents.
Table of Images 👆
- Exponent Rules Product of Powers
- Exponents Worksheets
- Powers and Exponents Worksheet
- Algebra Exponent Rules Worksheet
- Exponents Worksheets and Answers
- Powers and Exponents Worksheet
- Exponents Worksheets with Answers
- Negative Exponents Worksheet Answers
- 6th-Grade Exponents Worksheets
- Negative Exponents Worksheet with Answers
- Worksheets Exponent Quotient Rule
- Practice Exponent Rules Worksheet
- Fractional Exponents Worksheets
- Exponents Worksheets
- Negative Exponent Rule Worksheet
- Exponents and Polynomial Worksheets
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What are exponent rules?
Exponent rules are a set of rules that govern how exponents behave when performing arithmetic operations. Some of the key exponent rules include the product rule (a^m * a^n = a^(m+n)), the quotient rule (a^m / a^n = a^(m-n)), and the power rule ((a^m)^n = a^(m*n)). These rules help simplify expressions with exponents and make solving equations involving exponents more manageable.
What is the rule for multiplying exponents with the same base?
When you multiply exponents with the same base, you add the exponents together. This rule is known as the Product Rule of Exponents. So, if you have \( a^m \times a^n \), where \( a \) is the base and \( m \) and \( n \) are the exponents, the result is \( a^{m+n} \).
How do you divide exponents with the same base?
When dividing exponents with the same base, you subtract the exponents. This means that if you have x^a / x^b, where a and b are exponents and x is the base, you simplify it as x^(a-b).
What is the rule for raising a power to another power?
When raising a power to another power, you simply multiply the exponents together. This means that if you have a base raised to an exponent, and that entire expression is then raised to another exponent, the final exponent will be the product of the two exponents. For example, (a^m)^n = a^(m*n).
How do you simplify an exponent with a negative base?
To simplify an exponent with a negative base, you can rewrite the expression using the properties of exponents. If you have a negative base raised to an even power, the result will be positive. Conversely, if the negative base is raised to an odd power, the result will be negative. Simply evaluate the exponent and determine whether the result will be positive or negative based on whether the power is odd or even.
What is the rule for multiplying exponents with different bases but the same exponent?
When multiplying exponents with different bases but the same exponent, you can keep the same exponent and multiply the bases together. For example, if you have x^a * y^a, the result would be (x*y)^a. This rule allows you to simplify expressions by combining terms with the same exponent.
How do you simplify an exponent with a zero exponent?
To simplify an exponent with a zero exponent, you simply raise the base to the power of zero, which always equals 1. Therefore, any number or variable raised to the power of zero will simplify to 1.
How do you simplify an exponent with a negative exponent?
To simplify an exponent with a negative exponent, you can rewrite it as the reciprocal of the base raised to the positive exponent. This means that if you have a term like x^-n, you can rewrite it as 1/x^n. Remember that a negative exponent indicates that the base should be in the denominator, so flipping the fraction will make the exponent positive.
What is the rule for dividing exponents with different bases but the same exponent?
When dividing exponents with different bases but the same exponent, you can divide the bases and keep the exponent the same. For example, (a^m) / (b^m) = (a/b)^m. This rule applies when the bases are different but the exponents are the same.
How do you simplify an exponent with a fractional or decimal base?
To simplify an exponent with a fractional or decimal base, you can first convert the base to a fraction if it's a decimal. Then, you can use the properties of exponents to rewrite the exponent in a simpler form. For example, you can rewrite a fractional base raised to a negative exponent by flipping the base to the denominator and changing the exponent to positive. Similarly, for decimal bases, convert them to fractions and apply the exponent rules accordingly to simplify the expression.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.











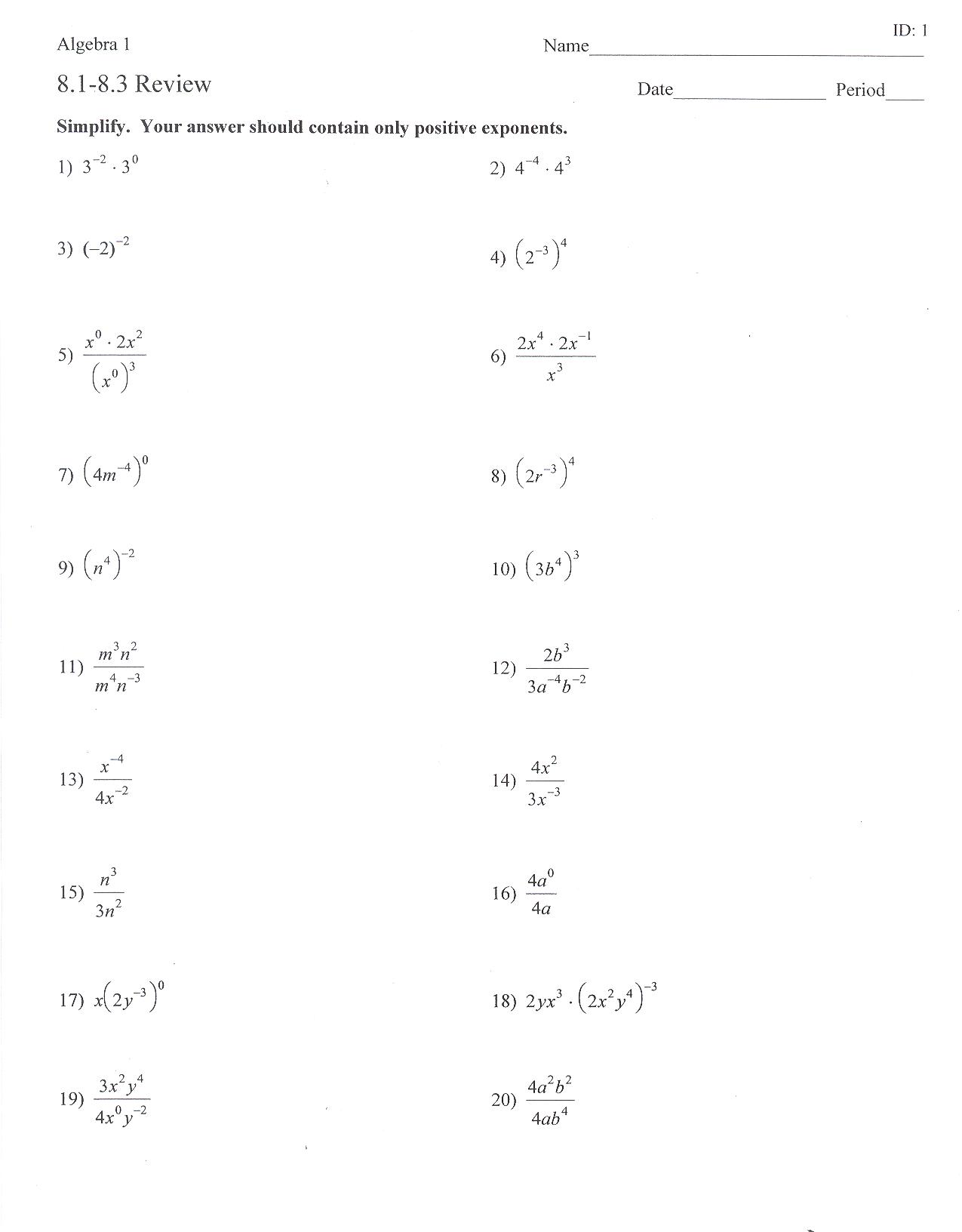






















Comments