Easy Multiplying Monomials Worksheet
Multiplying monomials can be a challenging concept for students to grasp, but with the right practice, it becomes much easier. This worksheet focuses specifically on multiplying monomials and is designed to help students strengthen their understanding of this mathematical operation. Whether you're a teacher searching for extra resources or a student wanting to improve your skills, this easy multiplying monomials worksheet is the perfect tool for you.
Table of Images 👆
- Factoring Polynomials Worksheet
- Exponents Worksheets and Answers
- Algebra Factoring Polynomials Worksheet
- Multiplying Binomials Worksheet
- Integers Multiplication Division Worksheet
- Polynomials with Negative Exponents Worksheets
- Factoring Monomials Worksheets
- Adding Polynomials Worksheet
- Factoring Trinomials Worksheet Coloring
- Algebra 1 Worksheets
- Decimal Multiplication Worksheets 4th Grade
- Subtracting Polynomials Worksheet
- 8th Grade Math Worksheets Algebra
- Order of Operations Worksheets 5th
- 6th Grade Math Worksheets Mean Median Mode
- Cross Multiplying Fractions Worksheets
- Fractions Math Aids Worksheets Answers
- Multiplying Numbers with Exponents
- 6th Grade Math Worksheets
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is a monomial?
A monomial is an algebraic expression that consists of only one term, which can be a constant, a variable, or a product of constants and variables raised to non-negative integer exponents.
How do you determine the degree of a monomial?
To determine the degree of a monomial, you simply add up the exponents of all the variables in the term. The sum of these exponents will give you the degree of the monomial. For example, in the monomial 3x^2y^3z, the degree is 2+3+1=6.
What are the rules for multiplying monomials with the same base?
When multiplying monomials with the same base, you add the exponents together. For example, when multiplying x^2 and x^3, you add the exponents to get x^(2+3) = x^5. This rule applies to any monomials with the same base, where you simply add the exponents to simplify the expression.
How do you multiply monomials with different bases?
To multiply monomials with different bases, you can simply multiply their coefficients and then combine the bases by adding their exponents if they are the same base. For example, to multiply 2x^3 and 3y^2, you would first multiply 2 and 3 to get 6, then combine the bases x and y by keeping them separate since they are different bases and you cannot simplify them further. So the result would be 6x^3y^2.
What is the product of a monomial and a constant?
The product of a monomial and a constant is also a monomial. When you multiply a monomial, which is a single term expression, by a constant, the result is simply the constant multiplied by the coefficients of the monomial, while keeping the same variable(s) and exponent(s) if present in the monomial.
How do you multiply monomials with multiple variables?
To multiply monomials with multiple variables, you simply multiply the coefficients together and multiply each variable with its corresponding exponent. For example, to multiply 3x^2y and 4xy^3, you would multiply 3x^2y * 4xy^3 = 12x^3y^4. Remember to add the exponents when variables have the same base.
What is the difference between the product of monomials and the sum of monomials?
The product of monomials involves multiplying two or more monomials together, resulting in a single monomial as the answer. On the other hand, the sum of monomials includes adding two or more monomials together, which may or may not simplify to a single monomial depending on whether the terms have similar variables and exponents. Ultimately, the product of monomials leads to a single monomial, while the sum of monomials may or may not simplify to a single monomial.
Can you simplify the product of monomials if they have the same exponents?
Yes, the product of monomials with the same exponents can be simplified by multiplying their coefficients together while keeping the same variables and exponents. This simplification allows us to combine like terms and express the result as a single monomial.
How do you handle negative exponents when multiplying monomials?
When multiplying monomials with negative exponents, you can rewrite the expression by moving the term with the negative exponent to the denominator and making the exponent positive. For example, if you have a term like "x^-2 * y^3", you can rewrite it as "y^3 / x^2" by moving "x^-2" to the denominator and changing its exponent to positive. This way, you can simplify the expression and perform the multiplication with positive exponents.
Is it possible to have a monomial with a variable raised to the power of zero?
Yes, it is possible to have a monomial with a variable raised to the power of zero. When a variable is raised to the power of zero, it simplifies to 1, resulting in a constant term. So, a monomial with a variable raised to the power of zero would be equivalent to a constant monomial.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.






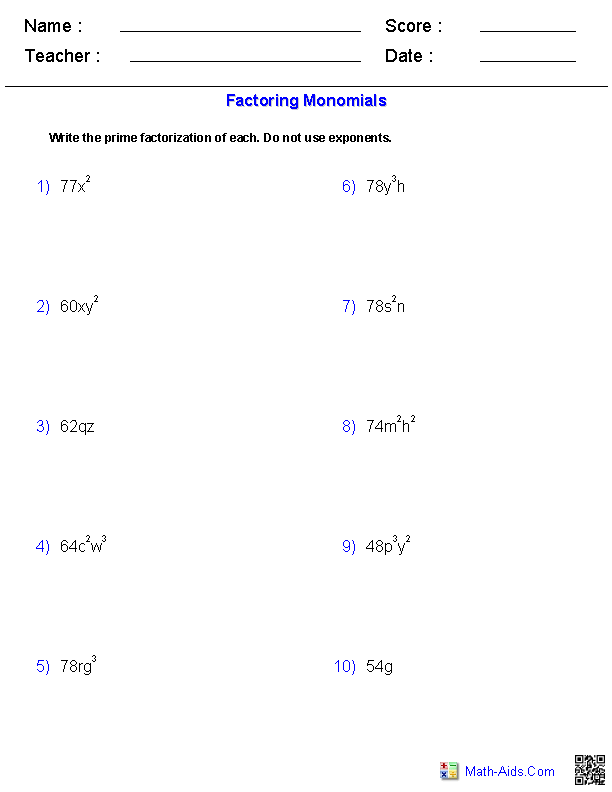

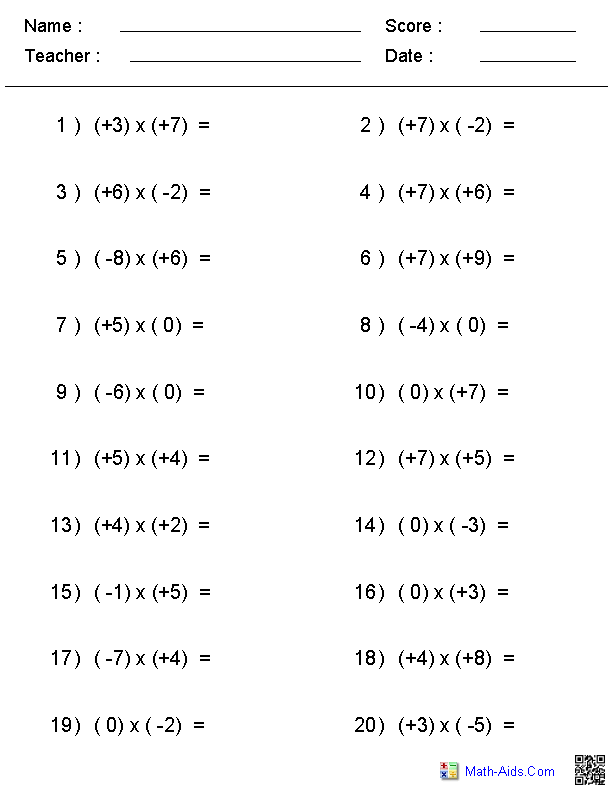
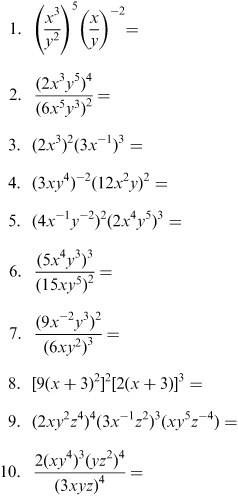



























Comments