Dividing Fractions Keep Change Flip Worksheet
Are you a math teacher searching for engaging resources to help your students understand the concept of dividing fractions? Look no further! We have just the worksheet you need. Entitled "Dividing Fractions Keep Change Flip Worksheet," this resource is designed to provide a clear and concise practice for students to master dividing fractions. With a focus on the important concepts of keeping the first fraction, changing division to multiplication, and flipping the second fraction, this worksheet is perfect for middle school students who are learning about fractions and want to strengthen their understanding of division.
Table of Images 👆
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
Why is it necessary to know how to divide fractions?
Knowing how to divide fractions is necessary because it allows us to solve complex mathematical problems, especially in real-life situations where fractions are commonly used. Dividing fractions helps in various mathematical operations, such as scaling recipes in cooking, calculating rates and proportions, and solving everyday problems involving quantities that are not whole numbers. Understanding how to divide fractions facilitates accurate and efficient problem-solving, helping us make decisions and analyze information effectively in many practical scenarios.
How do you divide a fraction by a whole number?
To divide a fraction by a whole number, you can convert the whole number into a fraction by placing it over 1. Then, flip the fraction you are dividing by and multiply it by the new fraction formed by the whole number. Simplify the result if possible by reducing to lowest terms.
Is it possible to divide a whole number by a fraction? If so, how?
Yes, it is possible to divide a whole number by a fraction. To do this, you can convert the whole number into a fraction by placing it over 1, and then use the rule that division is the same as multiplying by the reciprocal of the fraction. For example, if you want to divide 4 by 1/2, you convert 4 to 4/1 and then multiply by the reciprocal of 1/2, which is 2/1, giving a result of 4 x 2/1 = 8.
What is a reciprocal and how is it related to dividing fractions?
A reciprocal is the multiplicative inverse of a number, meaning that when you multiply a number by its reciprocal, the result is always 1. When dividing fractions, you actually multiply by the reciprocal of the second fraction. Instead of dividing by a fraction, you can multiply by its reciprocal to achieve the same result. This process makes dividing fractions simpler and involves multiplying by the reciprocal of the divisor.
Can you simplify the answer when dividing fractions? If so, how?
Yes, when dividing fractions, you can simplify the answer by first converting the division into a multiplication problem. To divide two fractions, you can multiply the first fraction by the reciprocal of the second fraction. After multiplying across the numerators and denominators, simplify the resulting fraction by reducing it to its simplest form by finding the greatest common factor between the numerator and denominator and dividing both by that factor.
What is the difference between dividing proper fractions and improper fractions?
The main difference between dividing proper fractions and improper fractions lies in the way the calculations are performed. When dividing proper fractions, the result is always a proper fraction with a value less than 1, whereas when dividing improper fractions, the result can be a proper fraction, a mixed number, or a whole number. Proper fractions have a numerator smaller than the denominator, while improper fractions have a numerator equal to or greater than the denominator.
How do you divide a mixed number by a whole number?
To divide a mixed number by a whole number, first convert the mixed number to an improper fraction. Then divide the numerator of the improper fraction by the whole number. Once you have the result, simplify if necessary. Remember to write the final answer as a mixed number if it is not a whole number.
When dividing mixed numbers, what is the step-by-step process?
When dividing mixed numbers, first convert the mixed numbers to improper fractions. Then, multiply the first fraction by the reciprocal of the second fraction. Next, simplify the resulting fraction if possible by reducing it to the lowest terms. Finally, if needed, convert the simplified fraction back to a mixed number. These steps will guide you through dividing mixed numbers efficiently.
Can you divide a fraction by another fraction? If so, how?
Yes, you can divide a fraction by another fraction by multiplying the first fraction by the reciprocal of the second fraction. To do this, take the first fraction, say \( \frac{a}{b} \), and divide it by the second fraction, say \( \frac{c}{d} \), you would multiply \( \frac{a}{b} \) by \( \frac{d}{c} \) to get the result of the division as \( \frac{a}{b} \times \frac{d}{c} = \frac{a \times d}{b \times c} \). This will give you the quotient of the two fractions.
How can dividing fractions be applied in real-life situations?
Dividing fractions can be applied in a variety of real-life situations such as baking in the kitchen to adjust recipe quantities, calculating medication dosages based on weight and concentration, determining fuel consumption rates for vehicles, or even dividing up a pizza or a cake into equal portions for a group of people. Essentially, whenever a situation involves dividing a quantity into equal parts or adjusting proportions, dividing fractions can be a useful and practical mathematical skill to apply.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.




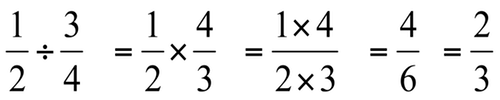

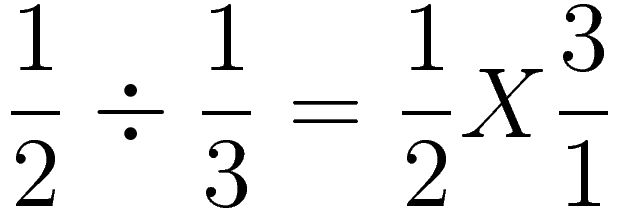














Comments