Dilation Worksheets for 8th Grade
If you're an 8th-grade student seeking practice with dilation, then these worksheets are just what you need. These worksheets focus on the concept of entity and subject in dilation, providing you with comprehensive exercises to enhance your understanding and skills.
Table of Images 👆
- 8th Grade Dilations Worksheet
- 8th Grade Math Dilations Worksheets
- Geometry Dilations Worksheet
- Dilation Math Worksheets
- Two-Step Transformations Worksheets
- Rotation Worksheet 8th Grade Math
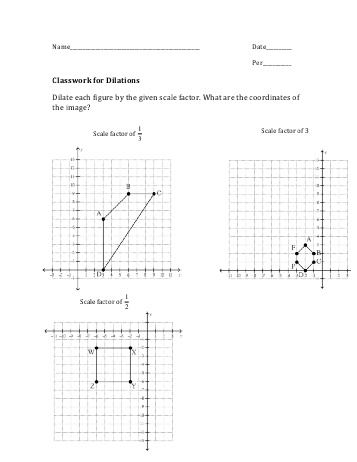
- 8th Grade Math Dilations Worksheets
- Geometry Dilations Worksheet
- Transformations Worksheets 8th Grade
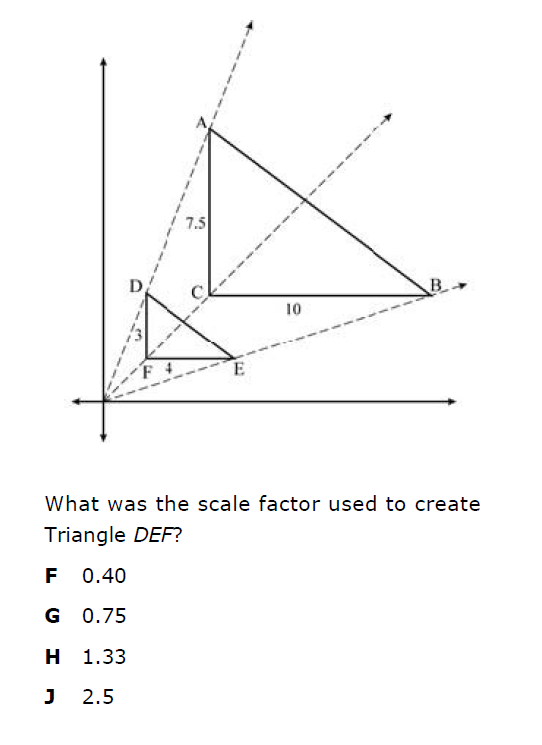
- 8th Grade Scale Factor Dilations Worksheet
- Geometry Rotations Worksheet
- 7th Grade Math Study
- Dilation Scale Factor Word Problems
- 8th Grade Math Slope Worksheets
- Transformation 8th Grade Math Worksheets
- 8th Grade Scale Factor Dilations Worksheet
- Surface Area and Volume Worksheet 8th Grade Math Practice
- 8th Grade Math Dilations Worksheets
More 8th Grade Worksheets
8th Grade Spelling Worksheets8th Grade Vocabulary Worksheets
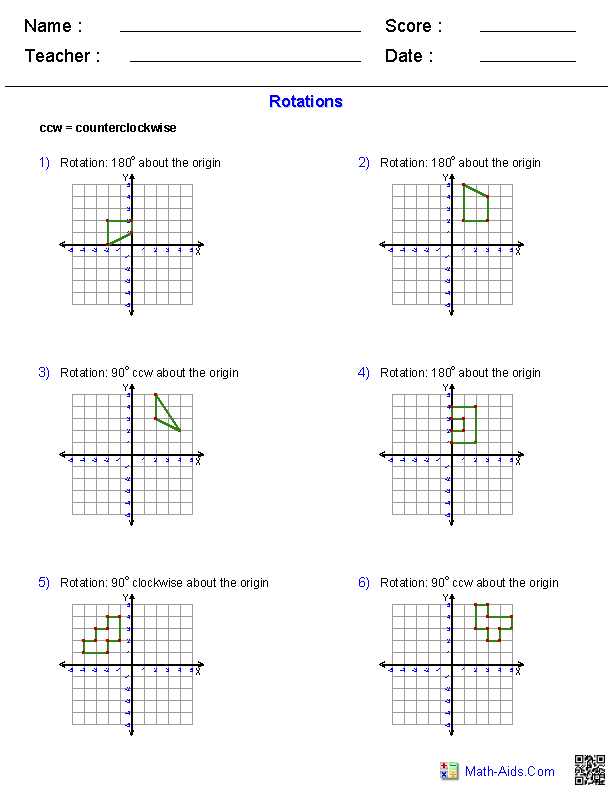
Rotations Worksheet 8th Grade
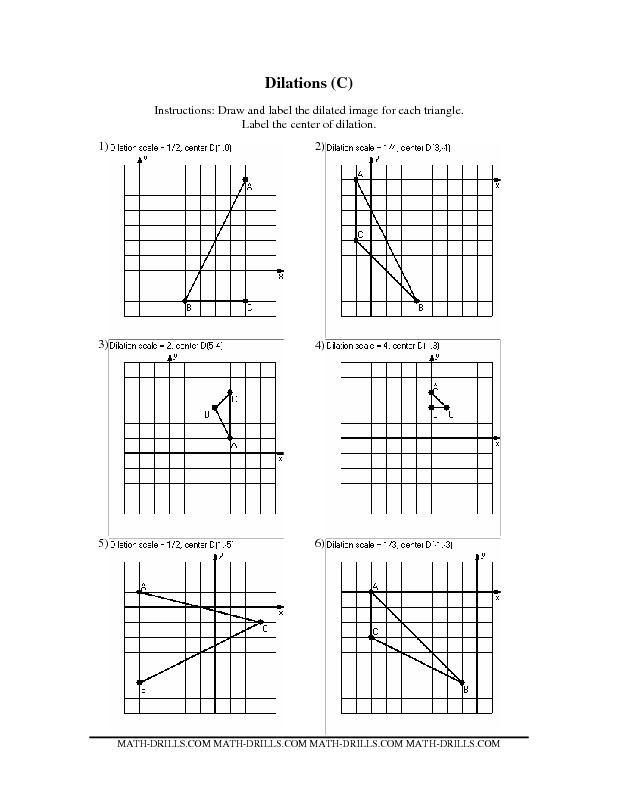
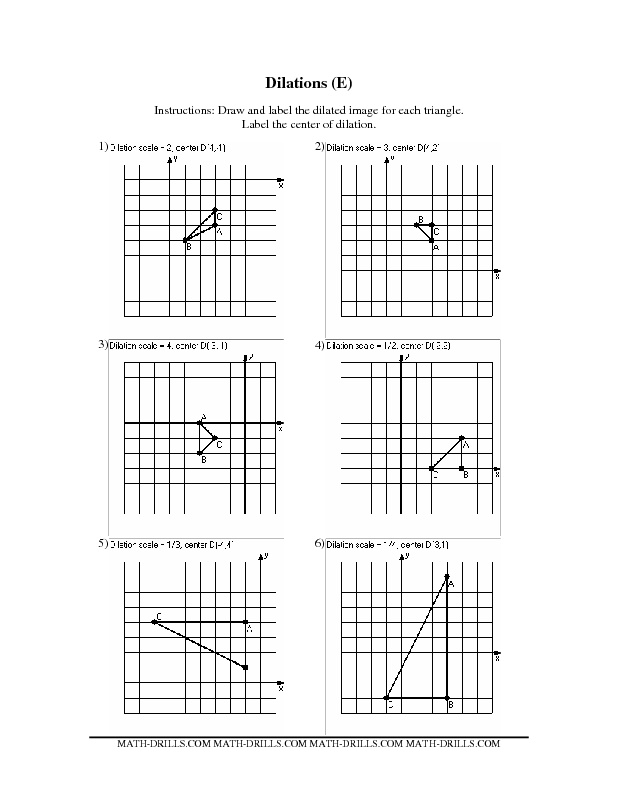
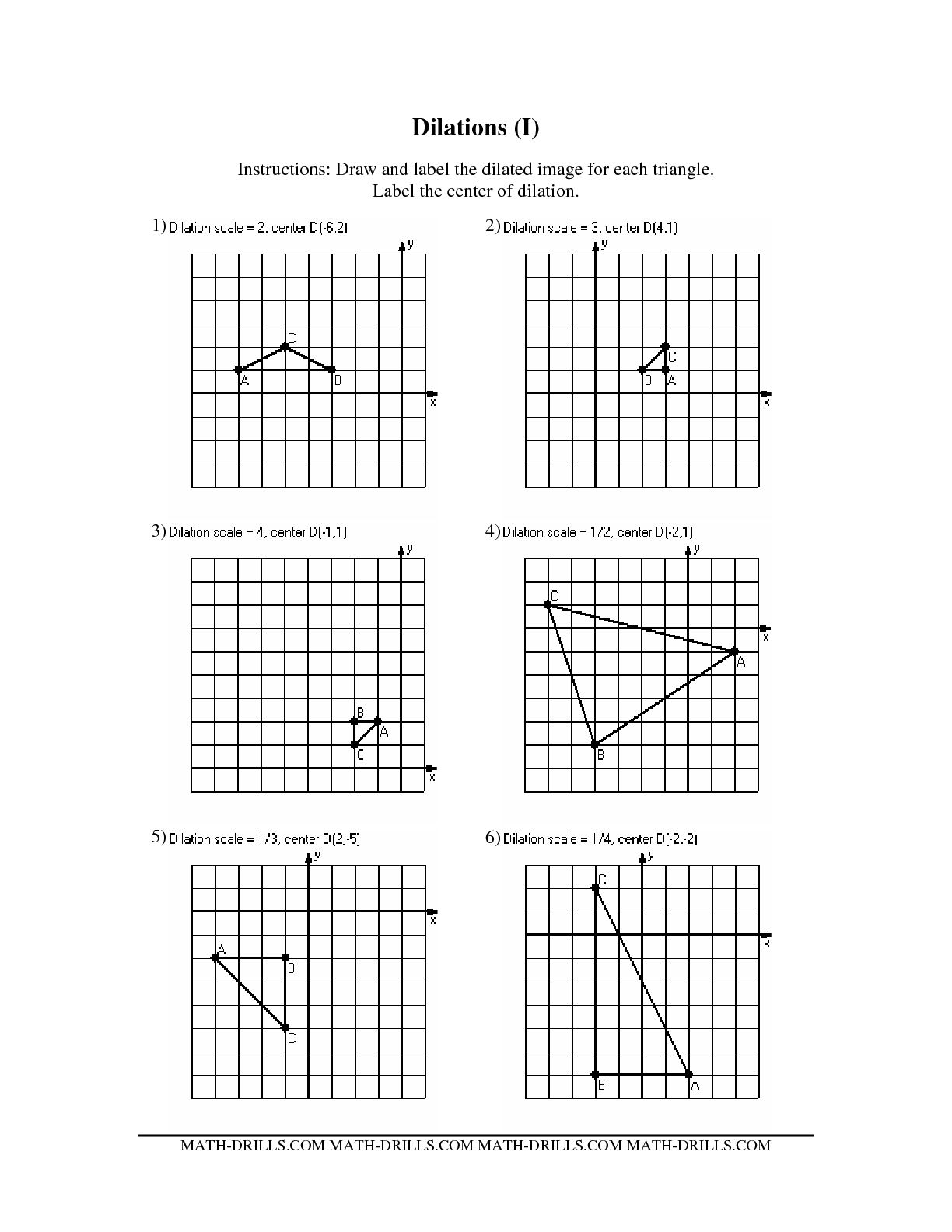
What is dilation in mathematics?
Dilation in mathematics is a transformation that changes the size of a figure, but not its shape. This transformation involves stretching or shrinking a shape by a specified scale factor along a particular direction. The center of dilation is usually specified, and all points on the figure are moved away from or towards this center by the same proportion.
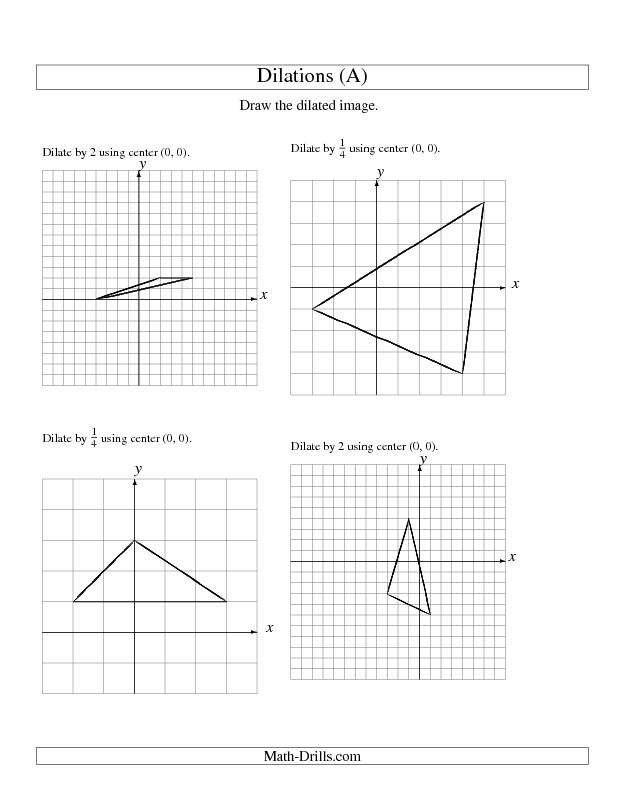
How does the scale factor affect a dilation?
The scale factor directly influences the size of a dilation. A scale factor greater than 1 will enlarge the figure, making it bigger than the original, while a scale factor between 0 and 1 will shrink the figure, making it smaller. A scale factor of 1 results in the figure remaining the same size. The scale factor determines the magnitude of the transformation in a dilation, impacting the proportions and dimensions of the original shape.
What is the difference between an enlargement and a reduction in a dilation?
In a dilation, an enlargement refers to increasing the size of the original figure by a scale factor greater than 1, while a reduction involves decreasing the size of the original figure by a scale factor between 0 and 1. Essentially, an enlargement makes the figure larger, while a reduction makes it smaller compared to the original figure being dilated.
How is the center of dilation determined in a figure?
The center of dilation in a figure is determined based on the point that serves as the fixed center from which all points in the figure are expanded or contracted. This point remains stationary while other points on the figure move away from or towards it with a certain scale factor. The center of dilation is crucial in understanding how the transformation affects the shape and size of the figure.
What is the relationship between the pre-image and the image in a dilation?
In a dilation, the pre-image is the original shape or figure, and the image is the resulting shape after it has been enlarged or reduced from the pre-image. The relationship between the two is that the image is a scaled version of the pre-image, where all corresponding points are either expanded or contracted by the same scale factor. This means that the image is similar to the pre-image, maintaining the same shape but with a different size.
How can dilations be used to determine the coordinates of transformed points on a coordinate plane?
Dilations can be used to determine the coordinates of transformed points on a coordinate plane by scaling the original coordinates with a specified factor. By multiplying the original x and y coordinates by the dilation factor, you can find the new coordinates of the transformed point. If the dilation factor is greater than 1, the point will be enlarged away from the origin, and if the factor is between 0 and 1, the point will be contracted towards the origin. The process of applying a dilation involves straightforward mathematical operations on the original point's coordinates, providing a clear and systematic way to calculate the new coordinates on a coordinate plane.
What is the formula for finding the coordinates of an image point after dilation?
The formula for finding the coordinates of an image point after dilation is (x', y') = (k * x, k * y), where (x, y) are the coordinates of the original point, k is the scale factor of dilation, and (x', y') are the coordinates of the image point after dilation.
What are the properties of a dilation in terms of angle measures and side lengths?
A dilation is a transformation that enlarges or reduces a figure proportionally. In terms of angle measures, a dilation preserves the measure of the angles in the original figure. However, in terms of side lengths, a dilation changes the lengths of the sides by the same scale factor. This means that if a figure is dilated by a scale factor of k, then all side lengths in the new figure will be k times greater or smaller than the corresponding side lengths in the original figure.
How are dilations related to similar figures and proportions?
Dilations are related to similar figures and proportions because when a figure is dilated by a scale factor, all of its corresponding sides and angles are enlarged or reduced proportionally. This means that dilations preserve the shape of the original figure, creating similar figures. Additionally, the scale factor of a dilation can be used to determine the proportions between corresponding lengths of the original and dilated figures. In summary, dilations maintain similarity between figures and allow for the comparison of their proportional relationships.
How can dilations be applied in real-life situations, such as scaling maps or resizing images?
Dilations can be applied in real-life situations such as scaling maps or resizing images by using a scale factor to increase or decrease the size of the original object while maintaining its proportions. For example, when scaling maps, a dilation can be used to enlarge or shrink the map to fit a specific size while preserving the relative distances between locations. Similarly, in resizing images, dilations can be applied to adjust the dimensions of the image without distorting its content, by multiplying the coordinates of each point by the scale factor to achieve the desired size change. By using dilations in such situations, accurate resizing and scaling of objects can be achieved effectively.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.





















Comments