Corresponding Angles Worksheet
Are you a math teacher or a student looking for a resource to help you practice corresponding angles? Look no further! This blog post presents a corresponding angles worksheet that will provide you with ample opportunities to strengthen your understanding of this important geometric concept. Whether you're learning about angles for the first time or need a refresher, this worksheet is designed to provide clear explanations and engaging practice problems to suit your needs.
Table of Images 👆
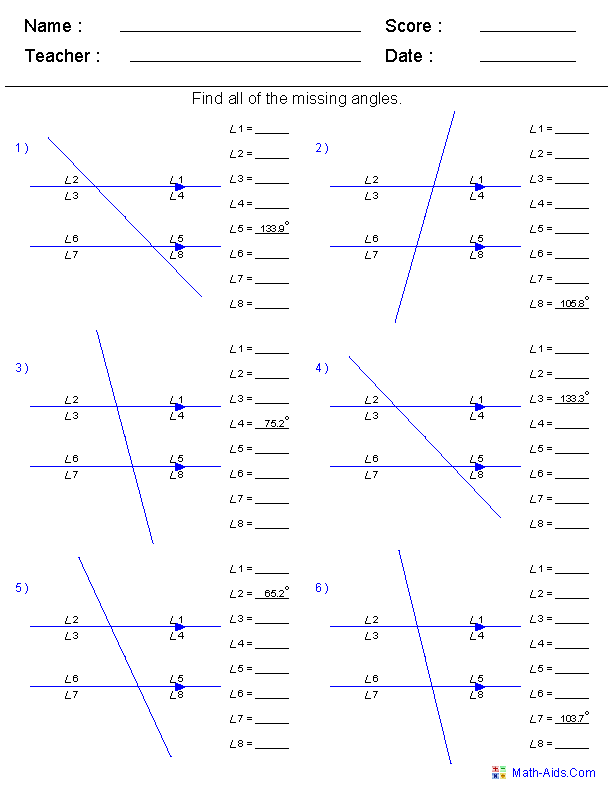
Missing Angle Worksheets
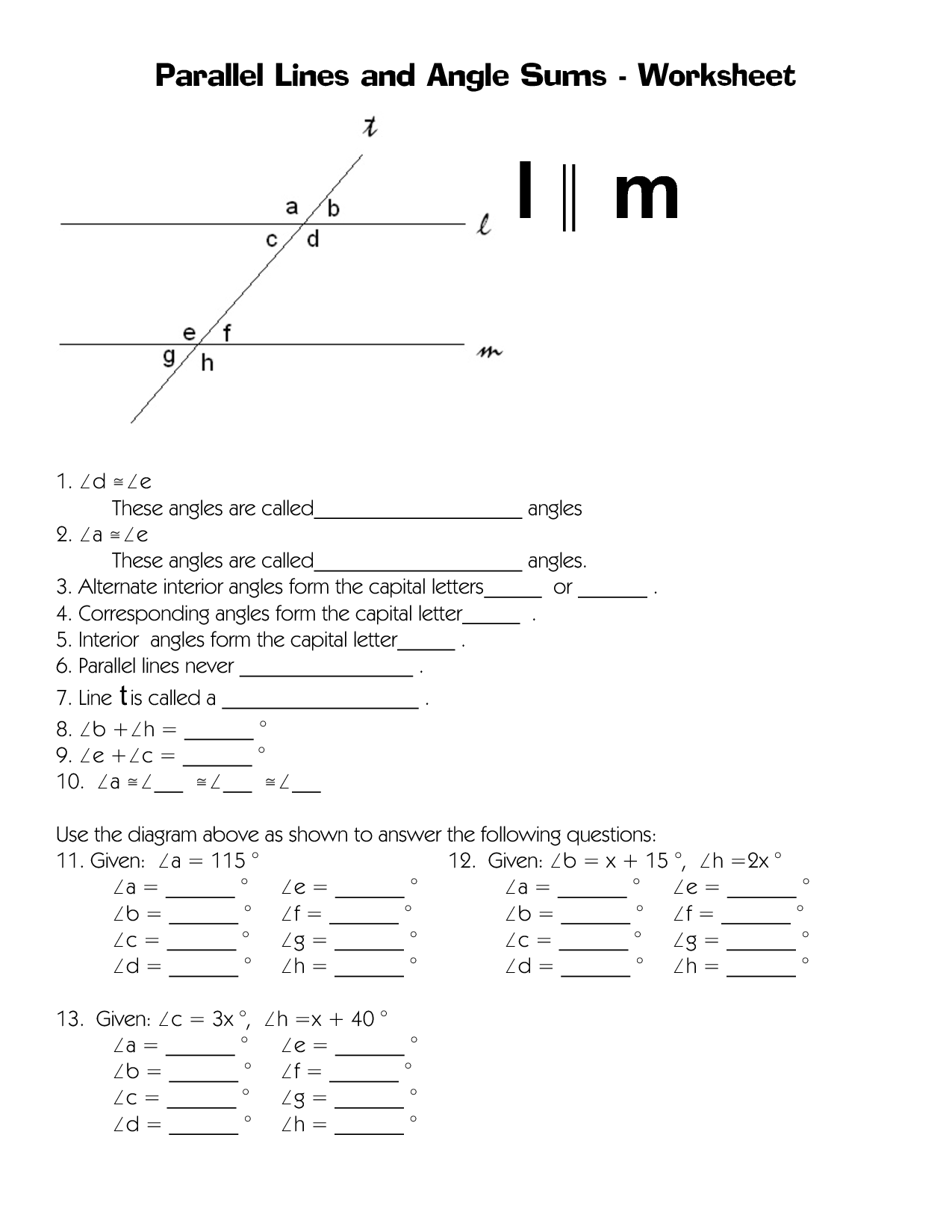
Parallel Lines and Angles Worksheet
Measurement Worksheets Grade 3
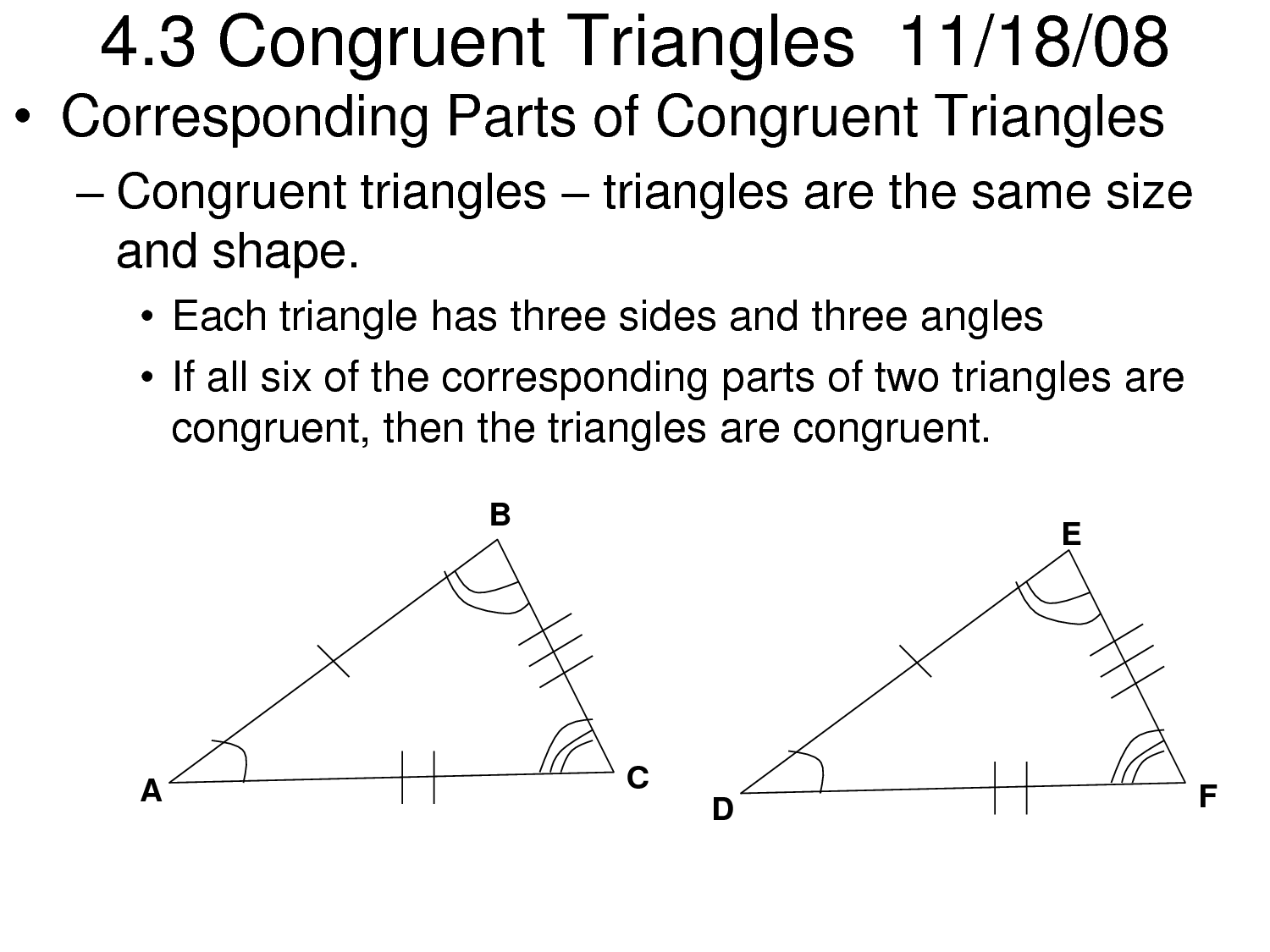
Congruent Triangles Worksheet
Identifying Angles Worksheets
What Are Corresponding Angles
Measuring Angles with a Protractor Worksheet
Similar Triangles Proportion Worksheet
How to Draw a Regular Concave Polygon
How to Draw a Regular Concave Polygon
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
All Amendment Worksheet
Symmetry Art Worksheets
Daily Meal Planning Worksheet
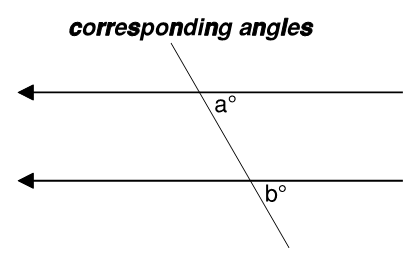
What are corresponding angles?
Corresponding angles are pairs of angles that are in the same position relative to a pair of parallel lines and are congruent, meaning they have the same measure. These angles are located on the same side of the transversal line and in the same relative position on each of the parallel lines.
How are corresponding angles related to parallel lines?
Corresponding angles are equal in measure when formed by a transversal intersecting two parallel lines. Therefore, corresponding angles are an important property of parallel lines as they help identify parallel lines and can be used to prove that lines are parallel.
How can corresponding angles be identified?
Corresponding angles are identified by being in the same position relative to a pair of parallel lines that are intersected by a transversal. They are located in matching corners on the same side of the transversal, with one angle being inside the parallel lines and the other being outside. Visually, corresponding angles have the same measure and are congruent to each other.
Why are corresponding angles important in geometry?
Corresponding angles are important in geometry because they help us identify and understand the relationships between parallel lines and transversals. By recognizing corresponding angles, we can determine if lines are parallel, utilize properties of angles to solve geometric problems, and prove mathematical theorems using theorems and postulates related to corresponding angles. Understanding corresponding angles is fundamental in geometry as it allows us to analyze geometric figures and relationships between angles in a systematic and logical manner.
What is the property of corresponding angles?
The property of corresponding angles is that when two lines are crossed by a third line (called a transversal), the angles in matching positions relative to the two lines are equal. In other words, if two angles are corresponding, they are in the same position in relation to the parallel lines being intersected by the transversal.
Can corresponding angles be congruent?
Yes, corresponding angles can be congruent. Corresponding angles are formed when a transversal intersects two parallel lines. These angles are in the same position in relation to the transversal and the parallel lines. When two parallel lines are intersected by a transversal, corresponding angles are congruent, meaning they have the same measure.
Do corresponding angles have the same measure?
Yes, corresponding angles have the same measure and are located in the same position at the intersection of two lines. When two lines are intersected by a transversal, corresponding angles are formed in matching positions on either side of the transversal, and these angles are congruent, meaning they have the same measure.
What is the relationship between corresponding angles and alternate interior angles?
Corresponding angles are located in the same position when two parallel lines are cut by a transversal, while alternate interior angles are located on opposite sides of the transversal and inside the two parallel lines. The relationship between the two is that they are congruent when the parallel lines are cut by a transversal, meaning that they have the same measure. In other words, corresponding angles and alternate interior angles are equal in measure when the lines are parallel and a transversal line is intersecting them.
How do corresponding angles help in solving geometric problems?
Corresponding angles are pairs of angles that are in the same relative position when two parallel lines are cut by a transversal. They are equal in measure, and this property can be used to solve geometric problems by applying the rules of parallel lines and angles. By recognizing corresponding angles and their relationships, we can use them to find missing angle measures, prove geometric theorems, and identify congruent or parallel lines in a diagram. Overall, corresponding angles play a crucial role in simplifying and solving various geometric problems efficiently.
Can corresponding angles be found in non-parallel lines?
No, corresponding angles can only be found in pairs of of parallel lines that have been intersected by a transversal line. In this case, the angles are in the same relative position at each intersection point. When lines are not parallel, corresponding angles cannot exist.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.
Comments