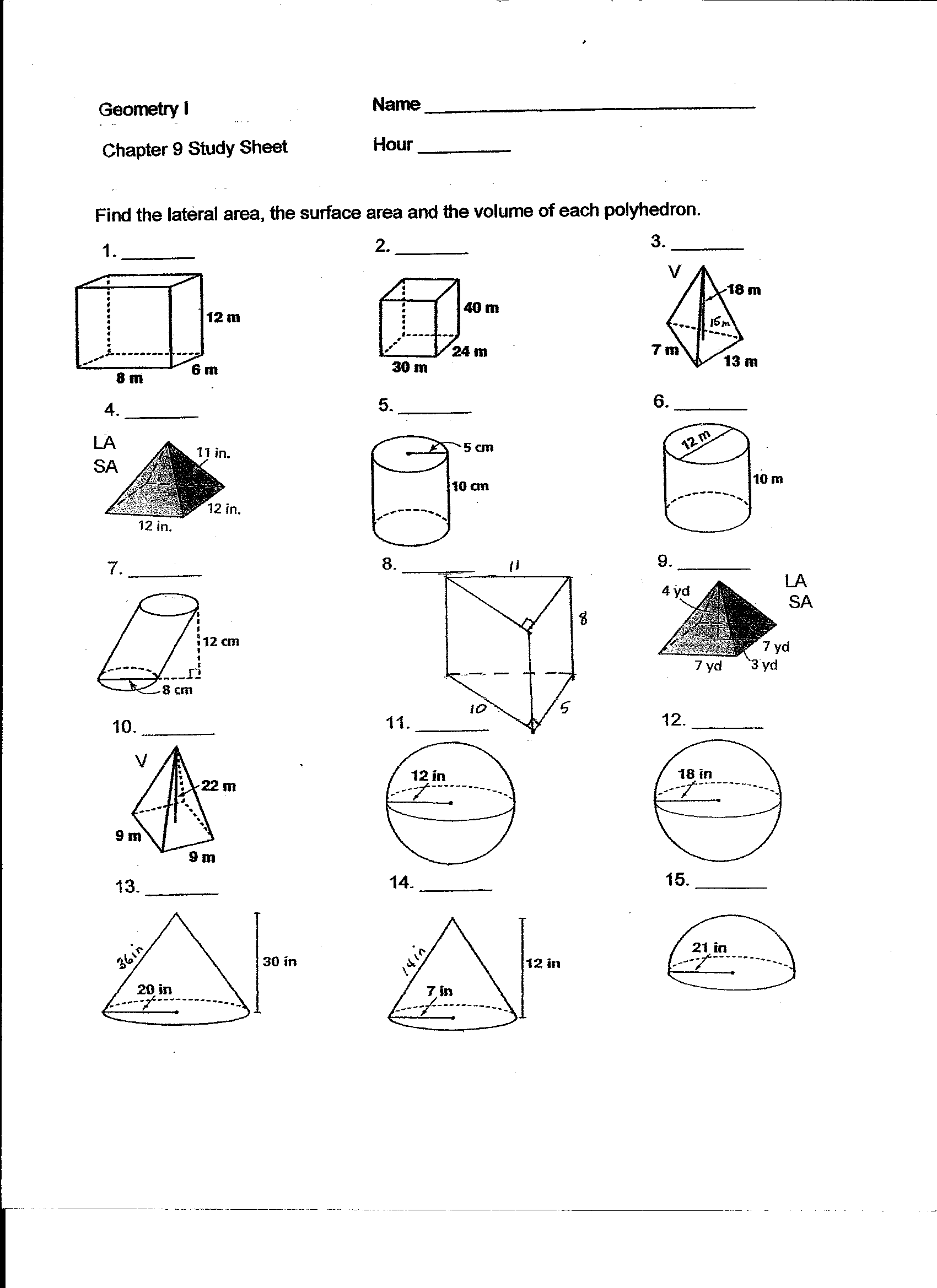
Cone Cylinder and Sphere Worksheet

Are you searching for a helpful and engaging resource to reinforce your knowledge of cones, cylinders, and spheres? Look no further! This comprehensive worksheet provides a variety of exercises that will test your understanding of these three-dimensional geometric shapes. Whether you are a student studying for an upcoming math test or a teacher looking for supplementary materials, this worksheet is the perfect tool to help you master these concepts.

  Surface Area Cylinder Worksheet

---

  Cone Cylinder Sphere

---

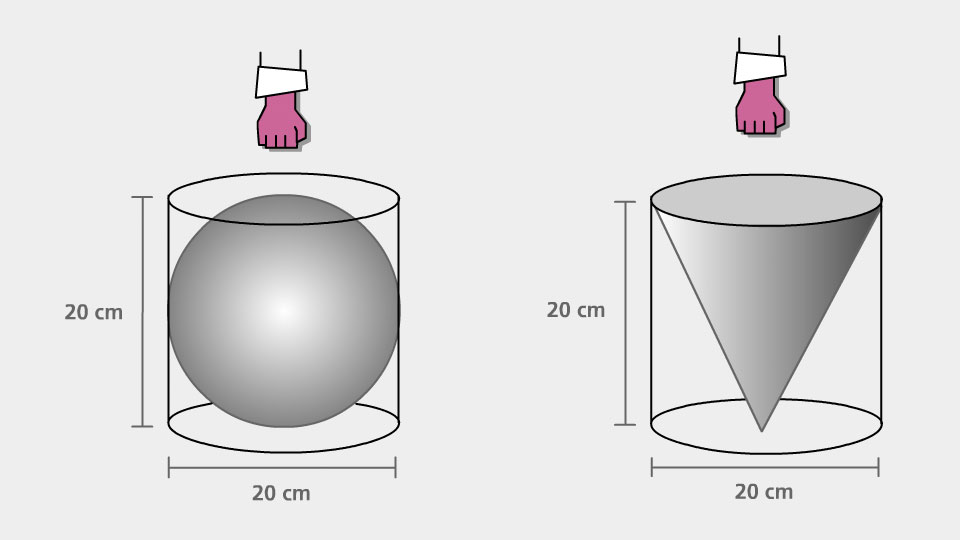
  Comparing Volumes of Cones Cylinders and Spheres

---

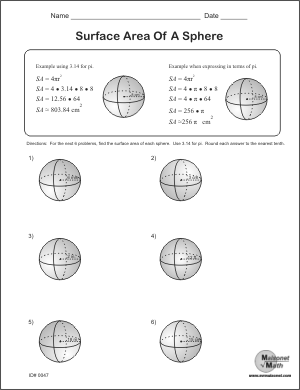
  Surface Area Cone Sphere Worksheet

---

  Surface Area Volume Worksheet

---

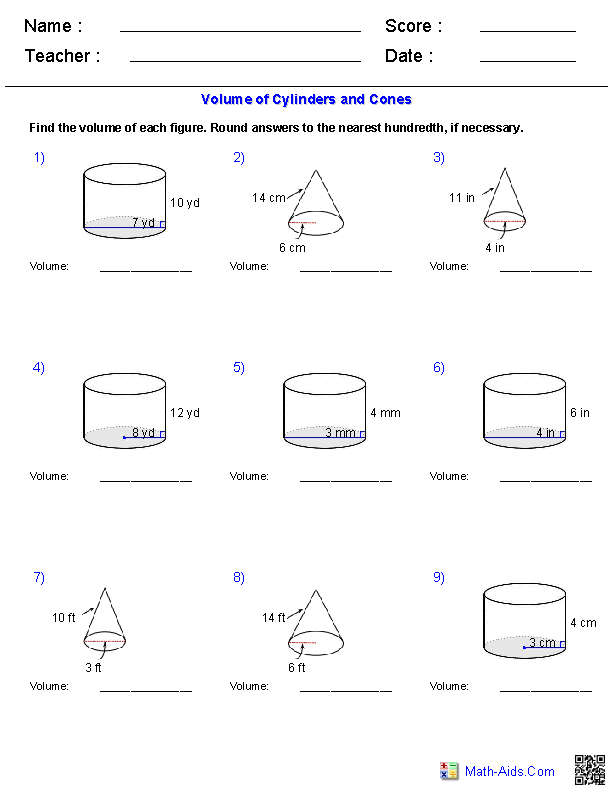
  Volume Cones and Cylinders Worksheet

---

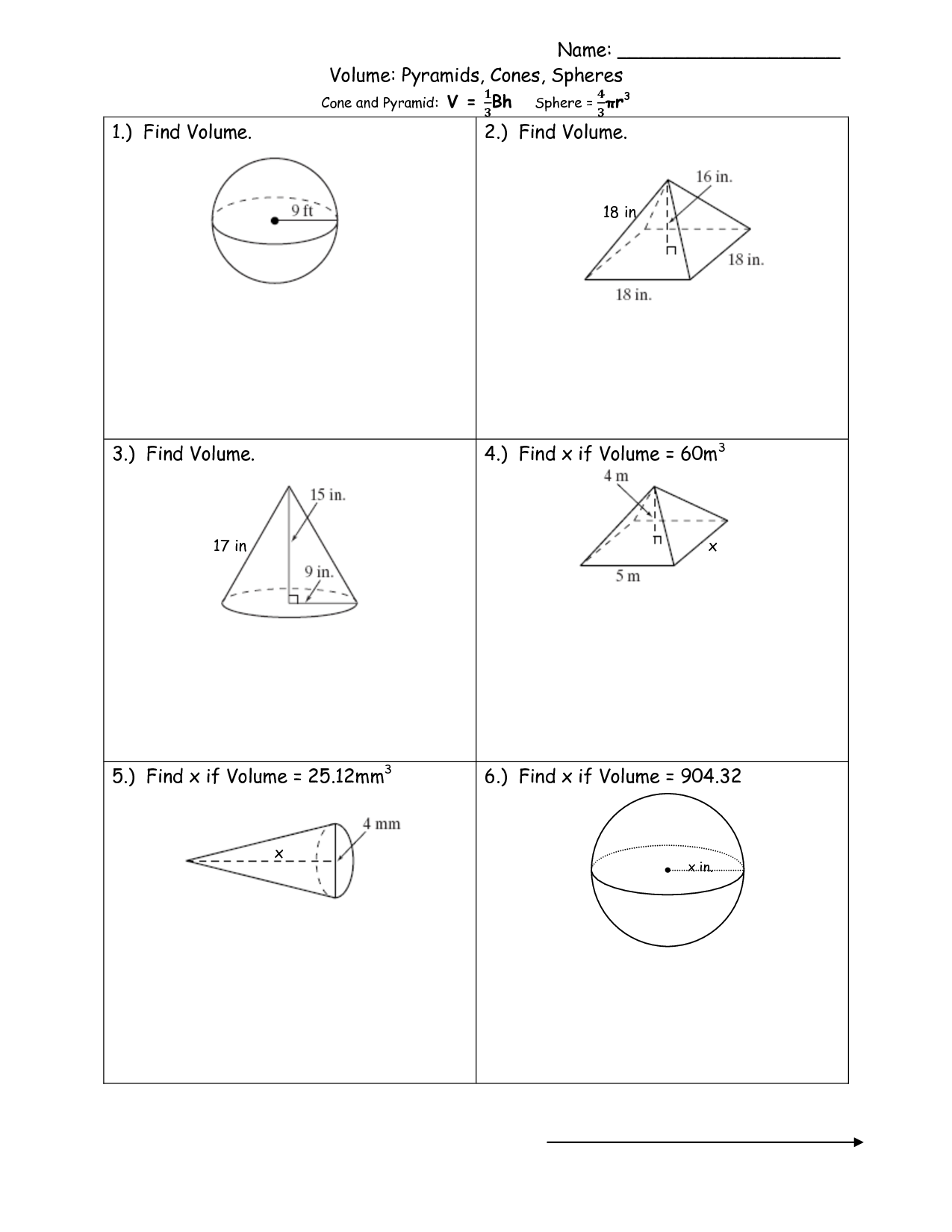
  Volume Pyramids Cones Spheres Worksheet

---

  Surface Area and Volume of Cones Worksheets

---

  Formula Volume Cone Sphere and Cylinder

---

  Volume Cylinders Cones and Spheres Worksheet

---

  Volume Pyramid Worksheet

---

  Cone Cylinder Sphere Cube Worksheet

---

  Volume Cylinders Cones and Spheres Worksheet

---

  Surface Area Volume Cylinder Worksheet

---

  Surface Area and Volume of Cones Worksheets

---

  Surface Area Volume Worksheet

---

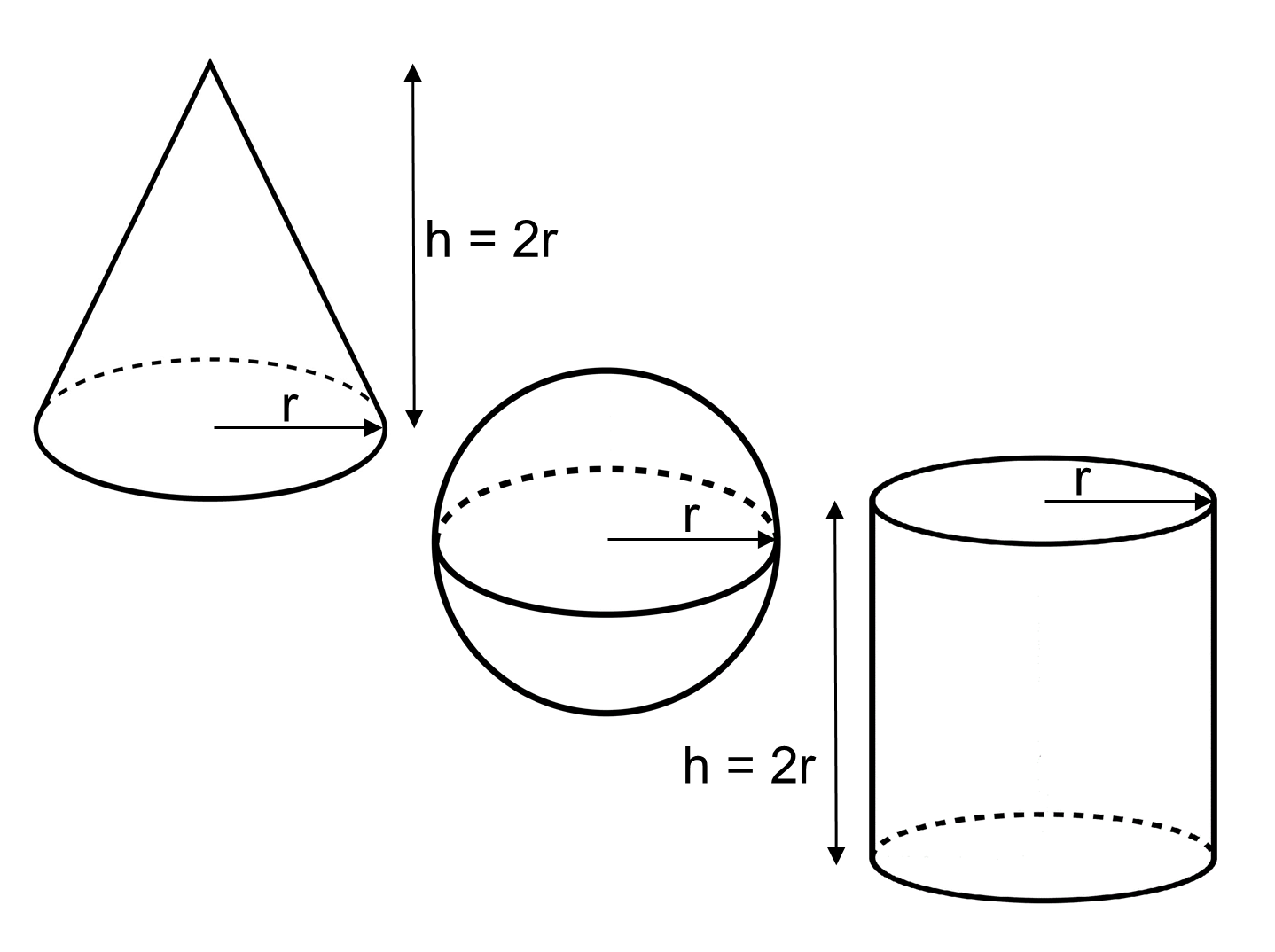
Describe the shape of a cone.

A cone is a three-dimensional geometric shape with a circular base that narrows to a single point called the apex. The side of the cone curves smoothly from the base to the apex, resembling a triangle with rounded sides.

What are the distinguishing characteristics of a cylinder?

A cylinder is a three-dimensional geometric shape that has two parallel and congruent circular bases connected by a curved surface. It has a constant cross-sectional shape along its entire height, and its height is perpendicular to the base. One distinguishing characteristic of a cylinder is that it has a curved surface that is not flat like a prism, but rather rounded. Additionally, cylinders have a fixed volume formula (V = ?r^2h), where r is the radius of the base and h is the height of the cylinder.

Explain the surface area of a sphere.

The surface area of a sphere is calculated using the formula 4?r^2, where r is the radius of the sphere. This formula represents the total area covered by the sphere's curved surface. It is a measure of how much space the surface of the sphere occupies and is used in various mathematical and scientific calculations involving spheres in geometry, physics, and engineering.

How do you calculate the volume of a cone?

To calculate the volume of a cone, you can use the formula V = (1/3)?r^2h, where V is the volume, r is the radius of the base of the cone, and h is the height of the cone. Simply plug in the values for the radius and height into the formula and calculate the volume using the appropriate operations.

Describe the curved surface area of a cylinder.

The curved surface area of a cylinder is the sum of the areas of its two circular bases and the lateral surface area formed by the curved part connecting the two bases. It can be calculated using the formula 2?rh, where r is the radius of the base and h is the height of the cylinder. This measurement represents the total area of the cylinder's outer surface excluding the bases.

What is the formula for finding the volume of a sphere?

The formula for finding the volume of a sphere is V = 4/3 * ? * r^3, where V is the volume, ? is a constant approximately equal to 3.14159, and r is the radius of the sphere.

Explain the relationship between the radius and height of a cone.

The radius and height of a cone are related through the Pythagorean theorem, where the slant height of the cone (which forms the hypotenuse of a right triangle with the radius and height) can be calculated using the formula: \( l = \sqrt{r^2 + h^2} \). Additionally, the height of the cone can also be expressed in terms of the slant height and the radius through the formula: \( h = \sqrt{l^2 - r^2} \). Therefore, the radius and height of a cone are intricately connected through these mathematical relationships.

How is the surface area of a cylinder calculated?

The surface area of a cylinder is calculated by adding the areas of the two circular bases and the lateral surface area. The formula for the surface area of a cylinder is 2?r² + 2?rh, where r is the radius of the base of the cylinder and h is the height of the cylinder.

Describe the volume of a sphere.

The volume of a sphere is calculated using the formula V = 4/3 * ? * r^3, where V represents volume and r is the radius of the sphere. This formula tells us how much space is enclosed within the spherical shape, representing the total amount of three-dimensional space the sphere occupies.

What is the formula for finding the total surface area of a cone?

The formula for finding the total surface area of a cone is given as A = ?r² + ?rl, where r is the radius of the base of the cone and l is the slant height of the cone.