Commutative and Associative Properties Worksheets
Are you a teacher or parent in search of engaging and effective ways to help your students or children understand the commutative and associative properties? Look no further! We have created a collection of worksheets specifically designed to reinforce the concept of these mathematical principles. By utilizing these worksheets, you can provide valuable practice opportunities for students, allowing them to better grasp the relationship between numbers and operations.
Table of Images 👆
- Math Properties Worksheets 6th Grade
- Associative Property of Multiplication Worksheets
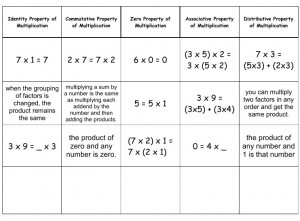
- Associative Property Multiplication
- Math Properties Worksheets 7th Grade
- Math Multiplication Property
- Math Addition Worksheets
- 4th Grade Math Worksheets PDF
- 4th Grade Math Worksheets PDF
- 4th Grade Math Worksheets PDF
- 4th Grade Math Worksheets PDF
- 4th Grade Math Worksheets PDF
- 4th Grade Math Worksheets PDF
- 4th Grade Math Worksheets PDF
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What is the commutative property of addition?
The commutative property of addition states that changing the order of addends does not change the sum, meaning that for any two numbers a and b, a + b is equal to b + a.
What is the commutative property of multiplication?
The commutative property of multiplication states that changing the order of the factors does not change the product. This means that for any numbers a and b, a * b = b * a.
What is the associative property of addition?
The associative property of addition states that when adding three or more numbers, the grouping of the numbers does not affect the sum. In other words, changing the order in which the numbers are grouped will not change the final result of the addition operation. For example, (2 + 3) + 4 is equal to 2 + (3 + 4), regardless of how the numbers are grouped.
What is the associative property of multiplication?
The associative property of multiplication states that the way in which numbers are grouped when multiplied together does not change the result. In other words, no matter how the numbers are grouped, the product will remain the same. For example, for any three numbers a, b, and c, (a × b) × c = a × (b × c).
Give an example of two numbers that demonstrate the commutative property of addition.
An example of two numbers that demonstrate the commutative property of addition is 3 and 5. When you add 3 and 5 together, you get 8 (3 + 5 = 8). Similarly, if you switch the order and add 5 and 3 together, you still get 8 (5 + 3 = 8). This shows that the order of the numbers being added does not affect the sum, illustrating the commutative property of addition.
Provide an example of two numbers that illustrate the commutative property of multiplication.
An example of two numbers that illustrate the commutative property of multiplication is 3 and 4. When you multiply 3 by 4, you get 12. Likewise, when you multiply 4 by 3, you also get 12. This demonstrates that the order of the numbers being multiplied does not affect the result, which is the essence of the commutative property of multiplication.
Give an example of three numbers that demonstrate the associative property of addition.
For the associative property of addition, choosing three numbers such as 2, 3, and 4 would be a suitable example. When adding the numbers in different groupings—(2+3)+4 and 2+(3+4)—the result will always be the same, demonstrating that the associative property holds true for addition.
Provide an example of three numbers that illustrate the associative property of multiplication.
Certainly! Let's consider the numbers 2, 3, and 4. When we multiply them, we can either associate the first two numbers first (2*3 = 6) and then multiply the result by the third number (6*4 = 24), or we can group the last two numbers first (3*4 = 12) and then multiply the result by the first number (2*12 = 24). In both cases, we get the same result showing the associative property of multiplication.
Explain why the commutative property is not applicable to subtraction.
The commutative property states that changing the order of the numbers being added or multiplied does not change the result. However, subtraction does not follow the commutative property because changing the order of the numbers being subtracted will typically result in a different answer. For example, 5 - 3 is not equal to 3 - 5. Subtracting involves finding the difference between two numbers, and the order in which the numbers are subtracted is important for getting the correct result.
Explain why the associative property is not applicable to division.
The associative property states that changing the grouping of elements being added or multiplied does not change the result. However, this property does not hold true for division because changing the grouping of elements being divided will often lead to different results. Division is not associative because the order in which numbers are grouped and divided affects the quotient obtained. In other words, changing the grouping of numbers being divided will likely yield different outcomes, making the associative property not applicable to division operations.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.






























Comments