Chapter 1 Geometry Worksheets

Geometry worksheets are a valuable resource for students and educators alike. These carefully crafted worksheets offer a wide range of exercises and problems that cover various topics within the subject of geometry. Designed to boost understanding and mastery of key concepts, these worksheets provide an opportunity for students to work independently or in a classroom setting. Whether you are a teacher looking for supplementary materials or a student seeking extra practice, these geometry worksheets are a beneficial way to reinforce learning and enhance subject comprehension.

  T-Shirts

---

  Geometry Conditional Statements Worksheet Answers

---

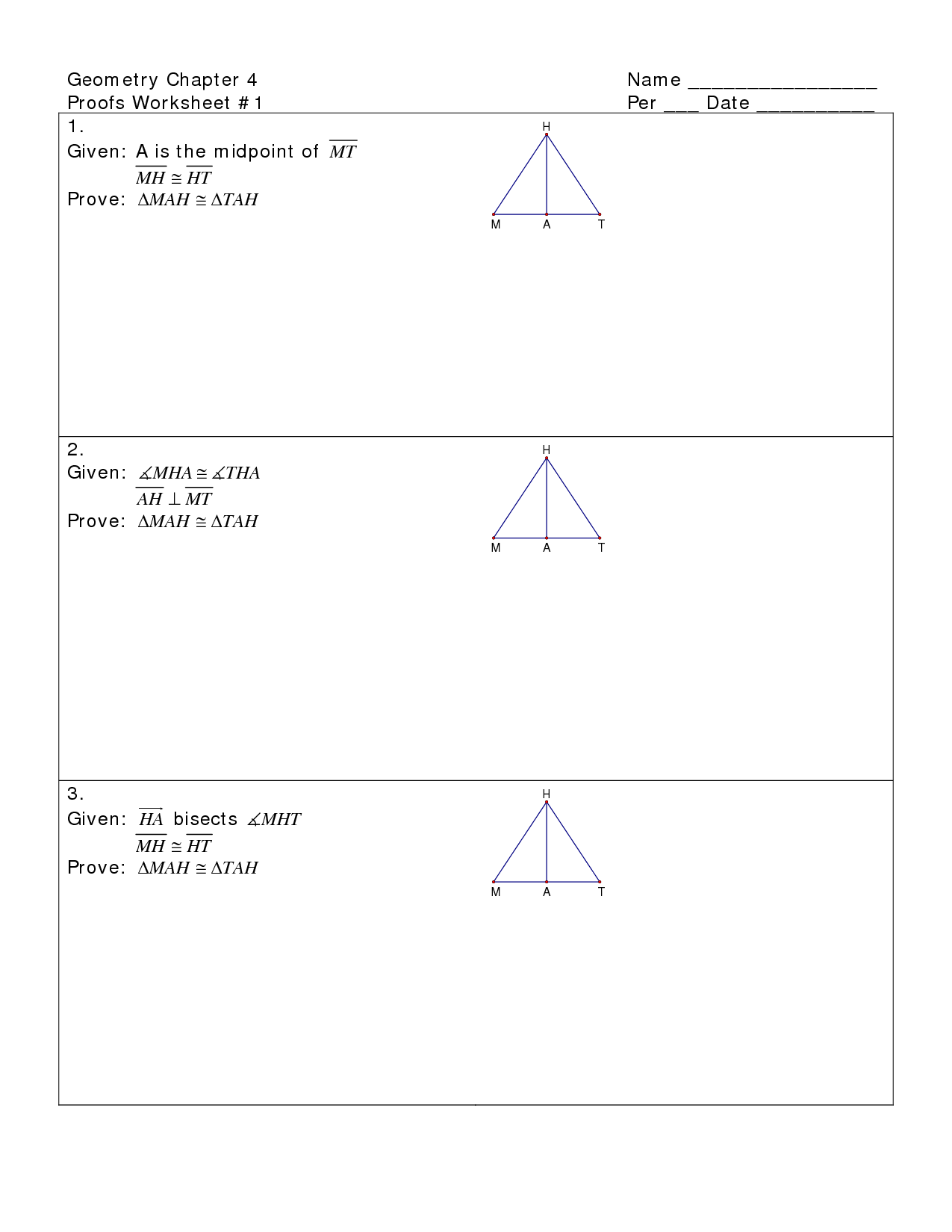
  Geometry Proofs Worksheets

---

  Geometry Chapter 3 Test Answers

---

  Prentice Hall Algebra 1 Worksheet Answers

---

  Geometry Proofs Practice with Answers

---

  Geometry Worksheet Answers Chapter 11

---

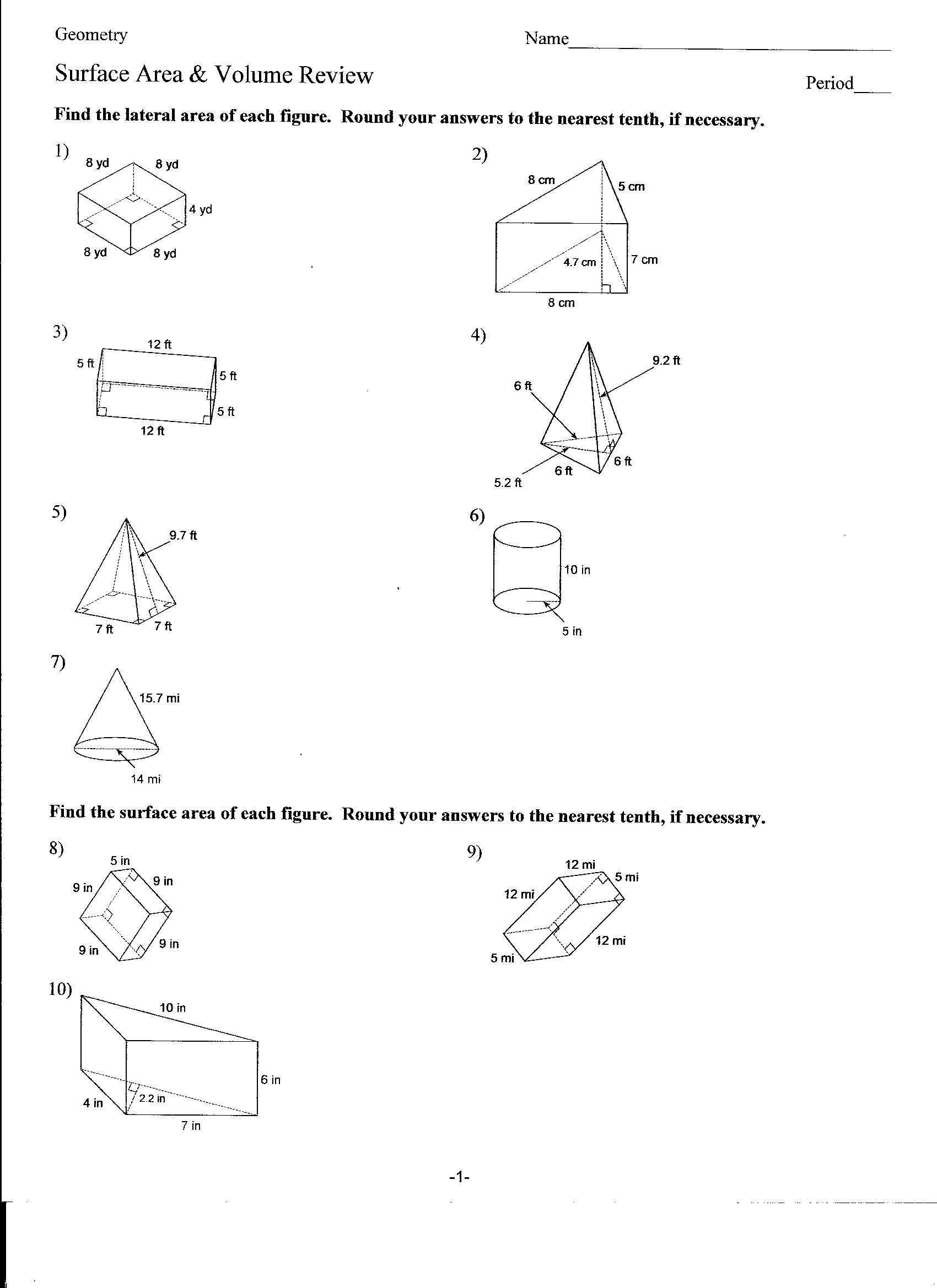
  Surface Area and Volume Worksheets

---

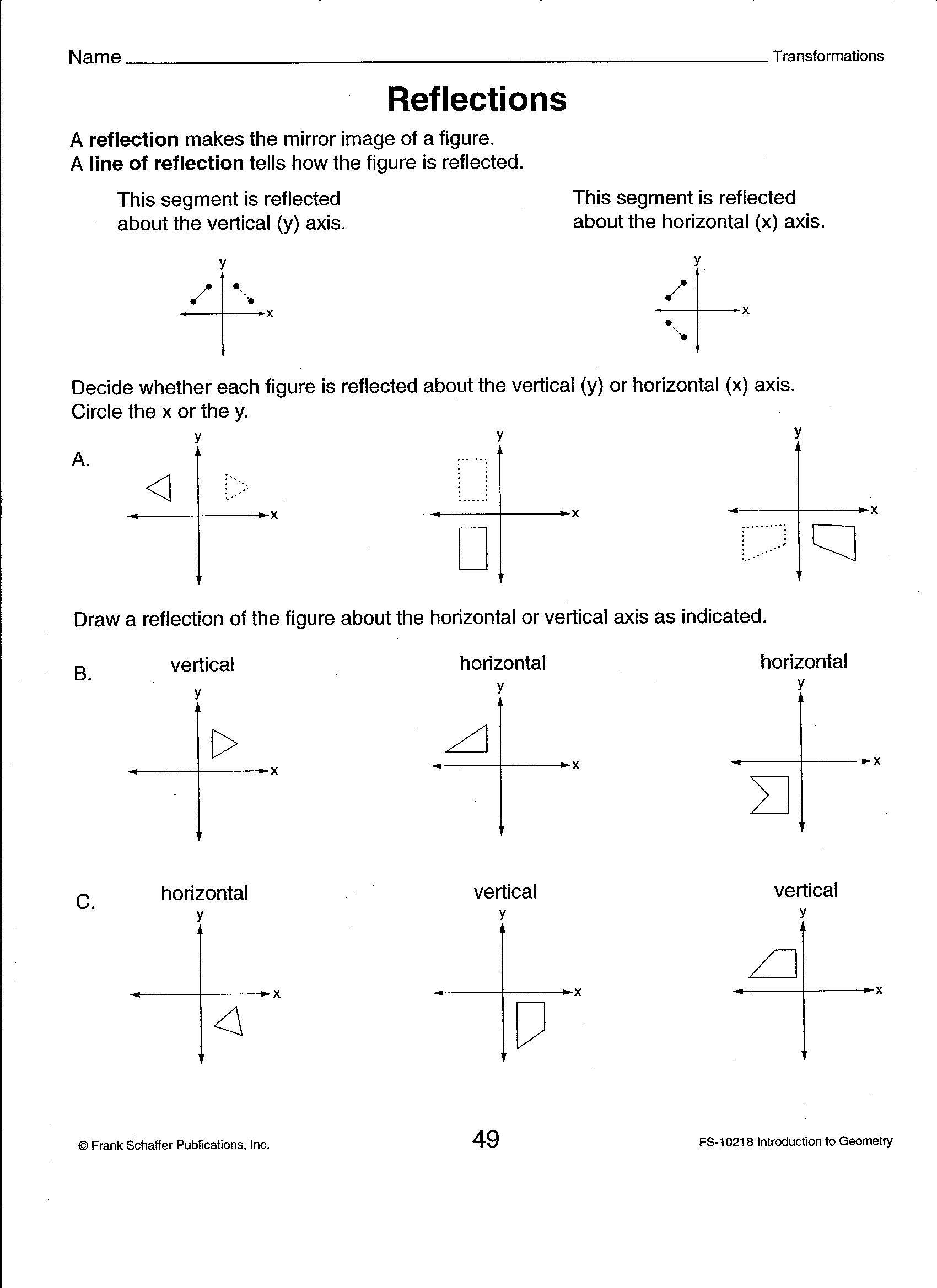
  Geometry Reflection Worksheet

---

  High School Geometry Worksheets

---

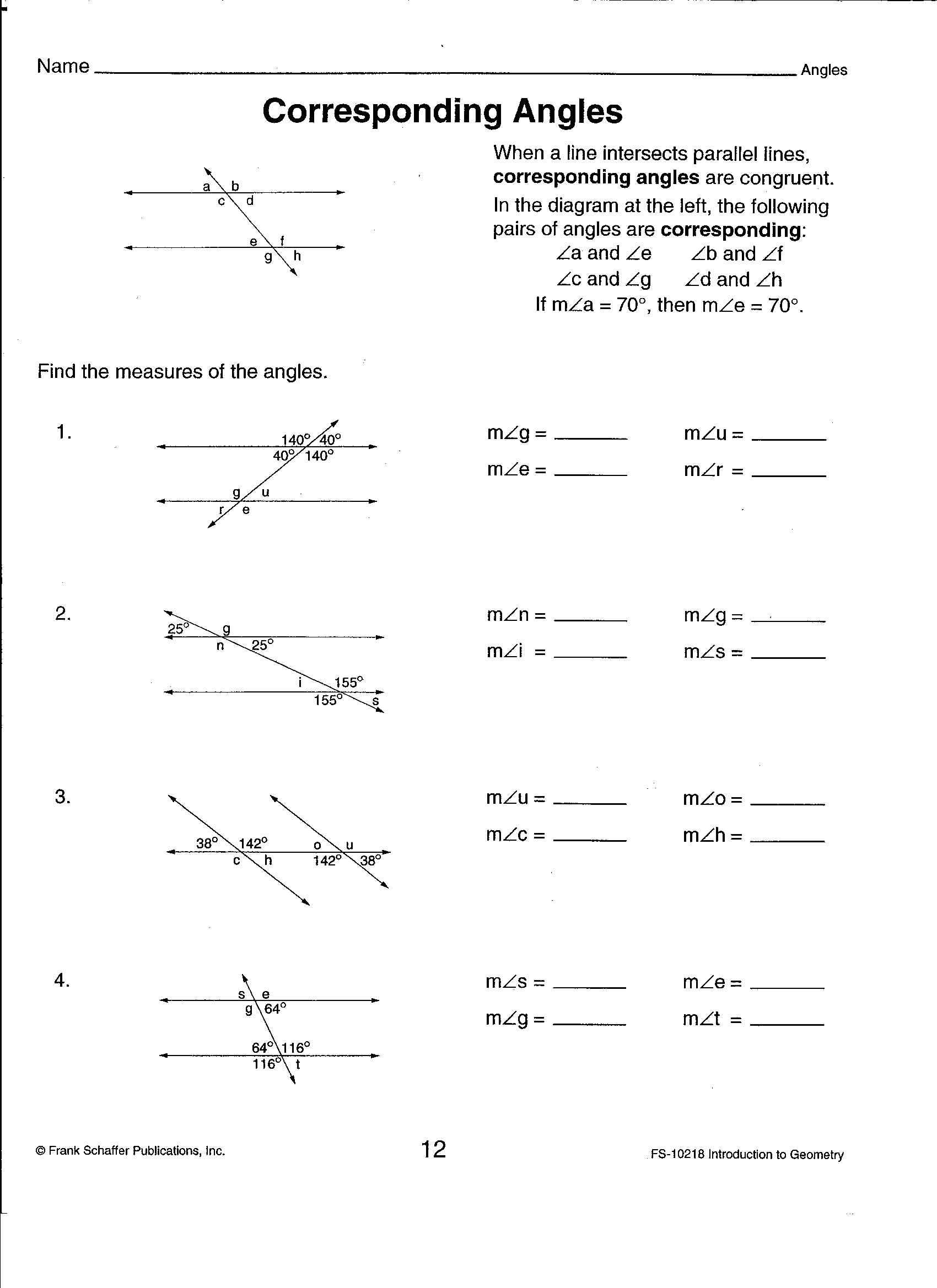
  Geometry Proving Lines Parallel Worksheet

---

  Geometry Points Lines and Planes Worksheets

---

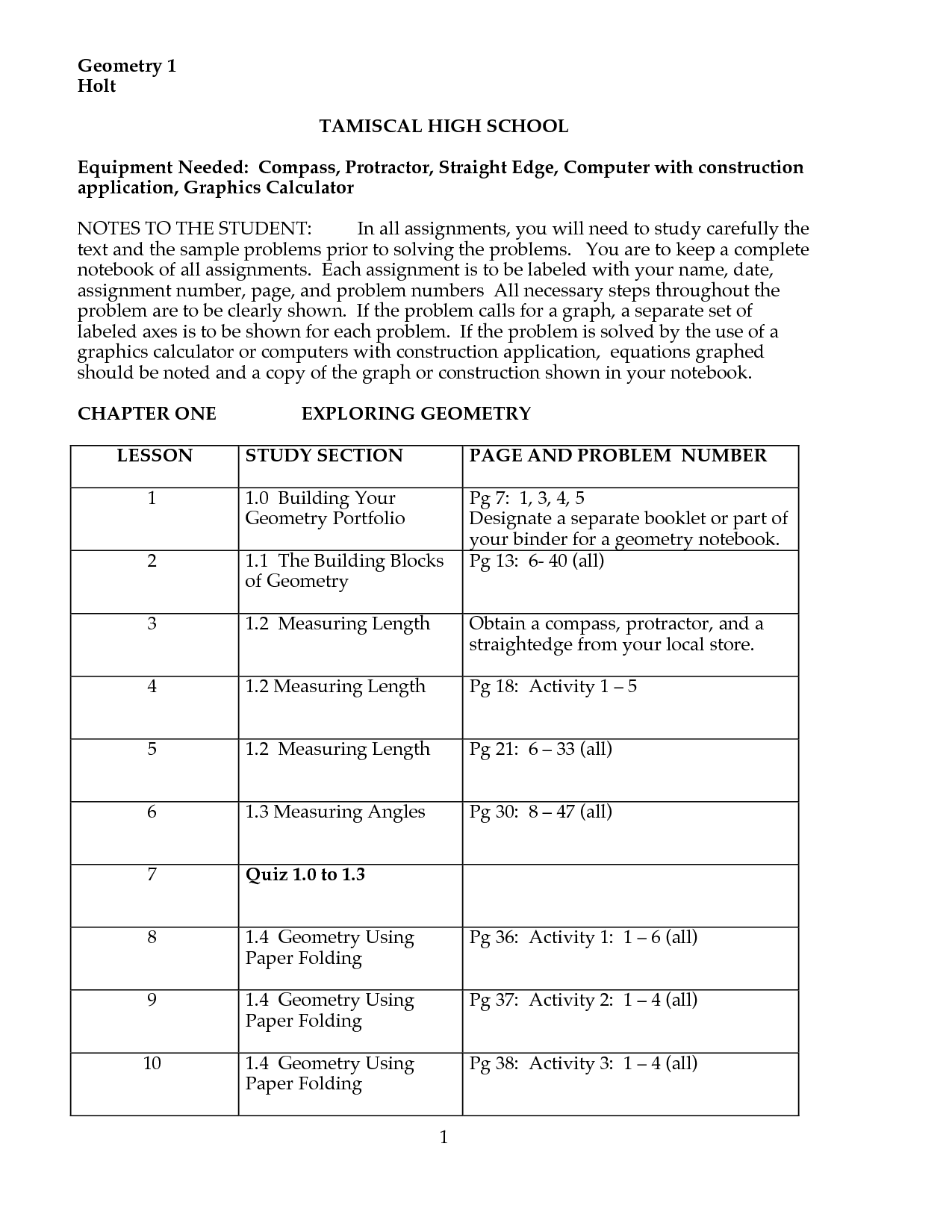
  Geometry Review Worksheet Chapter 1

---

  Glencoe Geometry Worksheets Answer Key for Chapter 1

---

  Glencoe Geometry Worksheet Answer Key

---

What is the definition of a point in geometry?

In geometry, a point is a location represented by a dot. It has no size, thickness, or dimensions, and is considered to be the most fundamental element in the field of geometry. Points are used to define lines, shapes, and objects in mathematical and geometric representations.

How are lines and line segments different?

Lines extend indefinitely in both directions, while line segments have two endpoints and a specific length. Lines have no thickness and are often represented by arrows at each end, whereas line segments are represented by a straight path between two defined points.

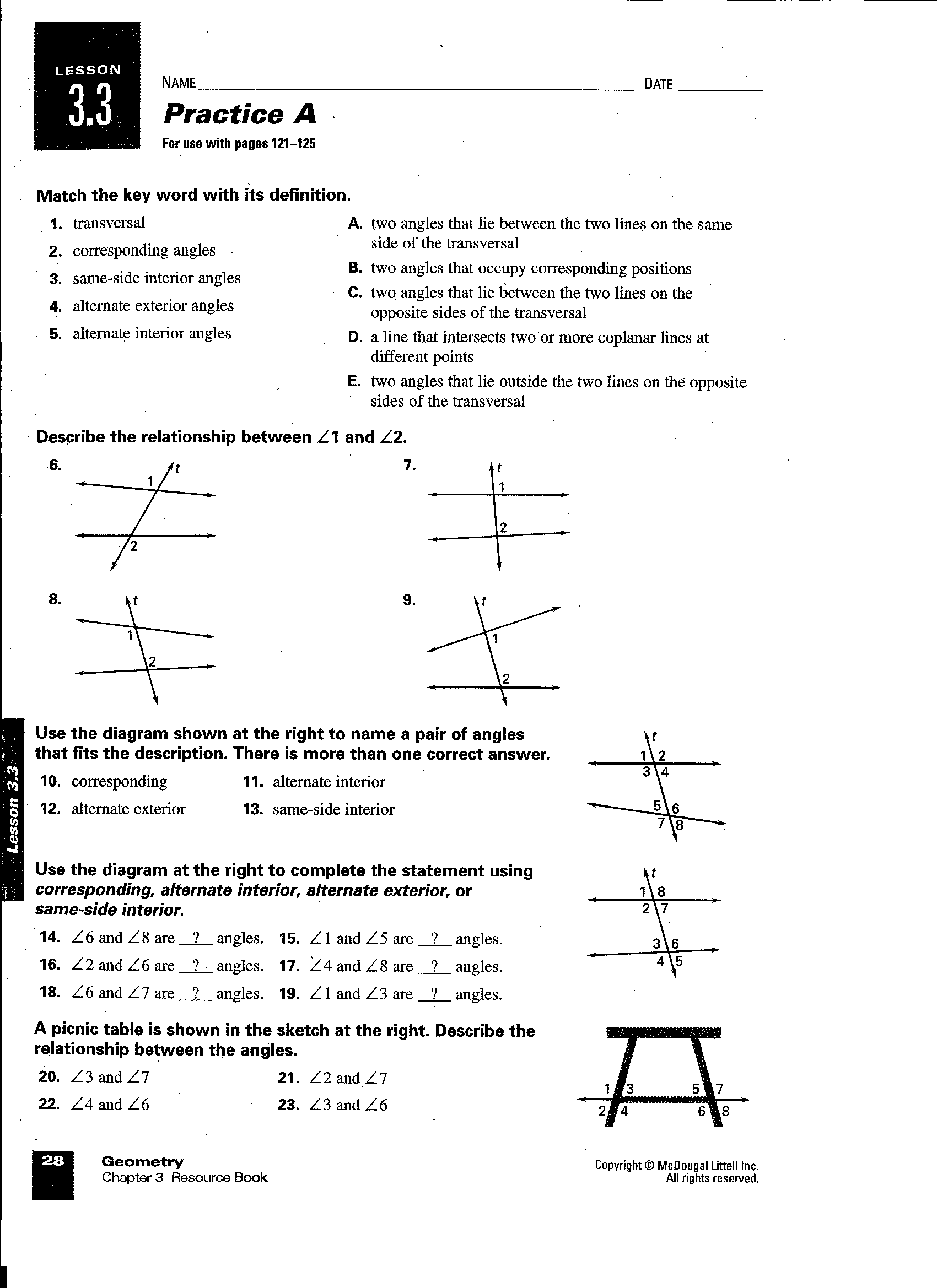
What is meant by parallel lines?

Parallel lines are lines in a plane that never intersect, regardless of how far they are extended. This means that they have the same slope and will always remain equidistant from each other.

How do you determine if two triangles are congruent?

Two triangles are congruent if all corresponding sides and angles of the triangles are equal in measurement. This can be determined using various methods such as side-side-side (SSS), side-angle-side (SAS), angle-side-angle (ASA), angle-angle-side (AAS), or hypotenuse-leg (HL) criteria. If the corresponding sides and angles of two triangles are equal, then the triangles are congruent.

What are the properties of a quadrilateral?

A quadrilateral is a polygon with four sides and four vertices. The sum of its interior angles is always 360 degrees. Additionally, the opposite sides of a quadrilateral are parallel, and the opposite angles are equal. Depending on the lengths of its sides and the measures of its angles, a quadrilateral can take various forms such as a square, rectangle, parallelogram, rhombus, trapezoid, or kite.

What are the different types of angles?

The different types of angles include acute angles (less than 90 degrees), right angles (exactly 90 degrees), obtuse angles (greater than 90 degrees but less than 180 degrees), straight angles (exactly 180 degrees), reflex angles (greater than 180 degrees but less than 360 degrees), and full angles or complete angles (exactly 360 degrees).

How do you calculate the area of a rectangle?

To calculate the area of a rectangle, you simply multiply the length of the rectangle by its width. The formula for calculating the area of a rectangle is A = length x width, where A represents the area of the rectangle.

What is the Pythagorean theorem and how is it used?

The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. Mathematically, it can be expressed as a^2 + b^2 = c^2, where c represents the length of the hypotenuse and a and b represent the lengths of the other two sides. This theorem is used to find the length of a side in a right-angled triangle when the lengths of the other two sides are known, or to determine whether a triangle is a right-angled triangle based on the lengths of its sides.

What is the formula to find the circumference of a circle?

The formula to find the circumference of a circle is 2?r, where r is the radius of the circle. Alternatively, the circumference can also be calculated using the formula C = ?d, where d is the diameter of the circle.

How do you find the volume of a rectangular prism?

To find the volume of a rectangular prism, you multiply the length, width, and height of the prism together. The formula is Volume = Length x Width x Height. Make sure to use the same units for each dimension, such as cubic centimeters or cubic meters, when calculating the volume of the rectangular prism.