Basic Trigonometry Worksheet

Trigonometry is a complex subject that requires a strong understanding of mathematical concepts and formulas. To help students grasp the fundamentals of trigonometry, a basic trigonometry worksheet can be a valuable tool. These worksheets are designed to provide practice problems and exercises that focus on the various topics within trigonometry, such as angles, triangles, and measurements. By offering a structured format for learning and practicing trigonometry, these worksheets can aid students in building their proficiency in this challenging subject.

  Trig Equations Worksheet

---

  Basic Trig Equations Worksheet

---

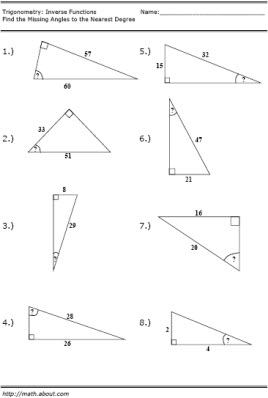
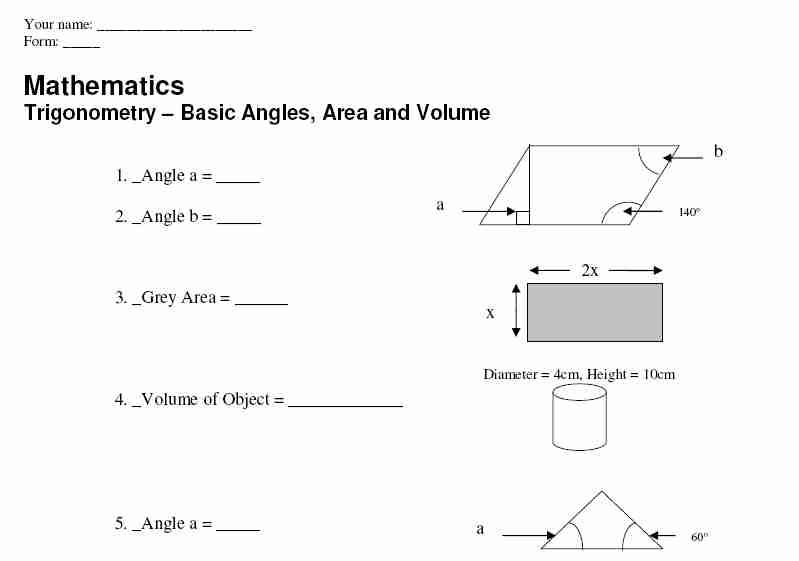
  Triangle Trigonometry Worksheet

---

  Trig Identities Practice Worksheet

---

  Trig Identities Worksheet

---

  Trigonometry Word Problems Worksheet

---

  Trig Identities Worksheet

---

  Trigonometric Ratios Worksheets

---

  Kuta Software Infinite Geometry

---

  Right Triangle Trig Ratios Worksheet

---

  Free Printable Trigonometry Worksheets

---

  Trig Derivatives Worksheet

---

  Basic Trig Identities Worksheet

---

  Free Basic Trigonometry Worksheets

---

What is the definition of trigonometry?

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles, particularly right-angled triangles. It involves studying the properties and functions of trigonometric ratios like sine, cosine, and tangent, and is used in various fields such as engineering, physics, and astronomy to calculate distances, heights, and angles.

How is a right triangle different from other triangles?

A right triangle is a type of triangle that has one angle measuring 90 degrees, known as a right angle. This distinguishes it from other triangles, where all angles are less than 90 degrees (acute triangle) or one angle is greater than 90 degrees (obtuse triangle). The side opposite the right angle is called the hypotenuse, and the other two sides are the legs of the right triangle.

What is the Pythagorean theorem and how is it used in trigonometry?

The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. In trigonometry, the Pythagorean theorem is used to define the trigonometric functions sine, cosine, and tangent. These functions are essential for solving problems involving angles and lengths of sides in right-angled triangles, as well as in various other applications in mathematics and physics.

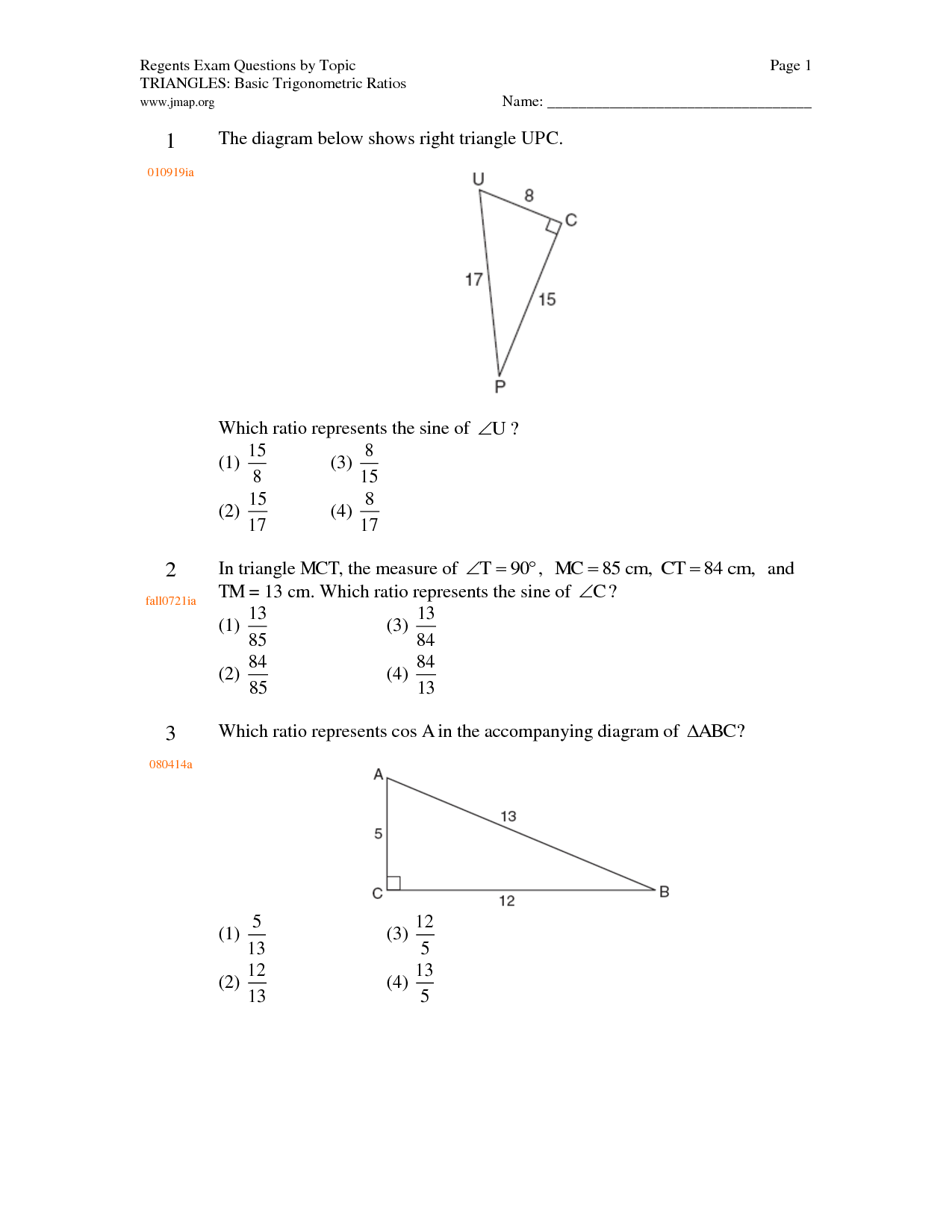
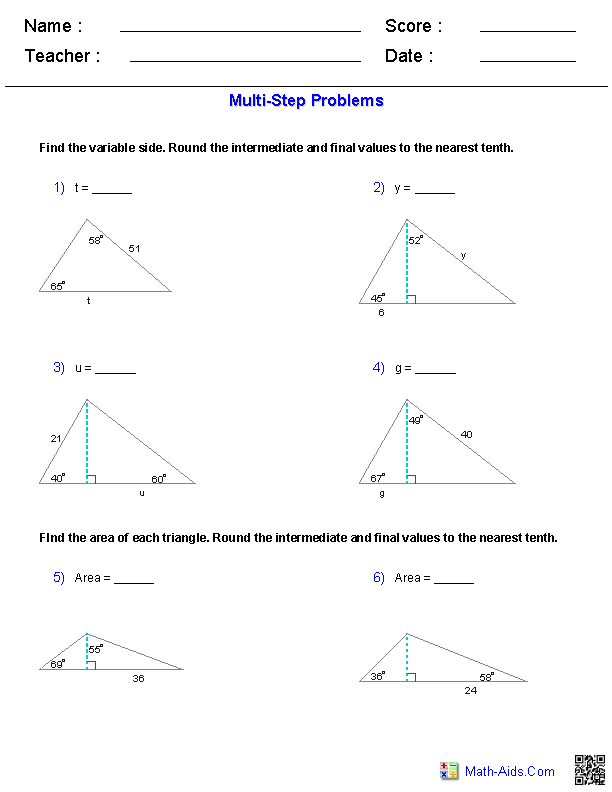
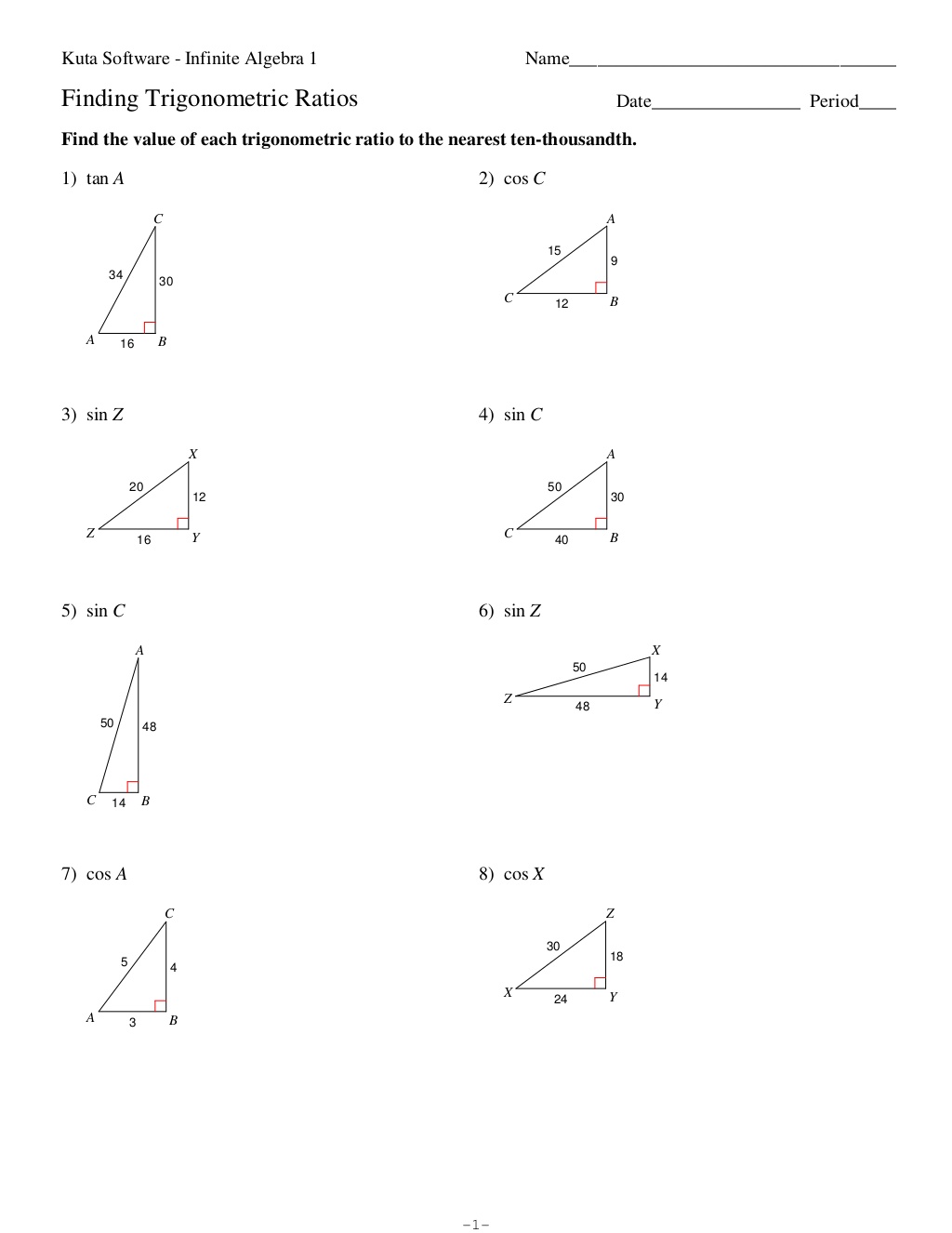
What are the three primary trigonometric ratios and how are they calculated?

The three primary trigonometric ratios are sine, cosine, and tangent. They are calculated as follows: sine = opposite/hypotenuse, cosine = adjacent/hypotenuse, and tangent = opposite/adjacent. These ratios are used in right-angled triangles to relate the angles to the sides of the triangle.

What is the unit circle and how is it used in trigonometry?

The unit circle is a circle with a radius of 1 centered at the origin of a coordinate system. It is used in trigonometry to relate the angles in a right triangle to the coordinates of points on the circle. By placing the unit circle on a coordinate system, trigonometric functions like sine and cosine can be defined in terms of the x and y coordinates of points on the circle. This allows for simplified calculations and a geometric understanding of trigonometric concepts.

What is the relationship between angles and trigonometric ratios?

Trigonometric ratios are defined based on the relative lengths of the sides of a right triangle and are used to relate angles in the triangle to those side lengths. These ratios, such as sine, cosine, and tangent, are functions of angles and provide a way to find missing sides or angles in a right triangle. Therefore, angles and trigonometric ratios are closely linked, as the values of the ratios depend on the specific angle involved in the problem.

How are special angles such as 30°, 45°, and 60° used in trigonometry?

Special angles such as 30°, 45°, and 60° are used in trigonometry as reference angles for common trigonometric functions. These angles have well-known exact values for sine, cosine, and tangent, making calculations simpler and more efficient. They are also used in determining trigonometric ratios, solving trigonometric equations, and in various applications in mathematics, physics, and engineering.

What is the difference between sine, cosine, and tangent functions?

Sine, cosine, and tangent are trigonometric functions used in mathematics to calculate the relationships between the angles and sides of a right triangle. The main difference lies in how each function represents these relationships. Sine represents the ratio of the length of the side opposite an angle to the hypotenuse, cosine represents the ratio of the length of the adjacent side to the hypotenuse, and tangent represents the ratio of the length of the opposite side to the adjacent side. In simpler terms, sine gives the vertical relationship, cosine gives the horizontal relationship, and tangent gives the slope or steepness of the triangle.

How can trigonometry be applied in real-world situations?

Trigonometry can be applied in various real-world situations such as architecture for designing buildings and bridges, engineering for constructing structures, navigation for determining locations using GPS, astronomy for studying celestial bodies, and physics for analyzing wave motions and oscillations. Additionally, trigonometry is used in industries like aviation for calculating flight paths, in surveying for measuring land, and in computer graphics for creating visually appealing images and animations.

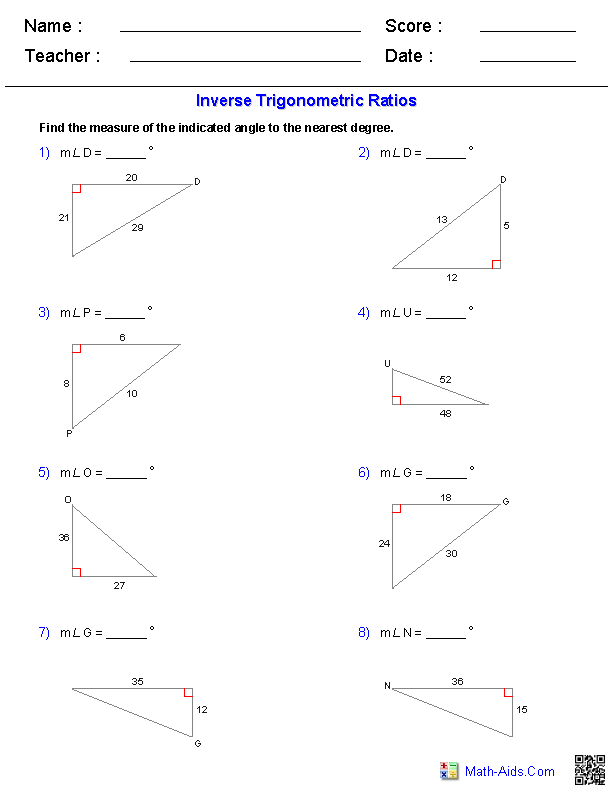
What are inverse trigonometric functions and how are they used?

Inverse trigonometric functions are mathematical functions that operate on the ratios of sides of a right triangle. They are used to find the angle of a right triangle given the lengths of its sides, thus providing a way to solve for angles in trigonometric equations. Inverse trigonometric functions such as arcsin, arccos, and arctan are used in fields like physics, engineering, and computer science to solve problems involving angles and trigonometric functions.