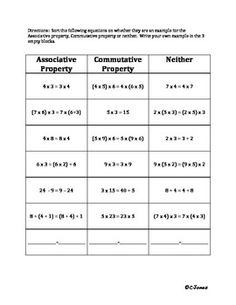
Associative Property Worksheets Printable

Are you searching for printable worksheets to help your students grasp the concept of the associative property? Look no further! In this blog post, we will explore a selection of worksheets designed to reinforce and practice the associative property with various math operations. These worksheets are suitable for teachers and homeschooling parents who want to provide their students with extra practice in understanding and applying this important mathematical concept.

  4th Grade Math Worksheets PDF

---

  Commutative and Associative Properties Worksheets

---

  Distributive Property Multiplication Worksheets

---

  Addition Properties 3rd Grade Worksheets

---

  Commutative and Associative Properties

---

  Math Worksheets Distributive Property

---

  Multiplication with Decimals Worksheets

---

  4th Grade Math Worksheets Fractions

---

  Addition and Subtraction Worksheets 3rd Grade

---

  Multiplication Sign Dot

---

  Multiplication Table Chart 50X50

---

  Multiplication Table Clip Art

---

What is the associative property of addition?

The associative property of addition states that changing the grouping of numbers being added does not change their sum. In other words, when adding three or more numbers together, you can regroup them in any way and the sum will remain the same. For example, (2 + 3) + 4 is the same as 2 + (3 + 4), both equaling 9.

What is the associative property of multiplication?

The associative property of multiplication states that when performing multiple multiplication operations on a set of numbers, the result will be the same regardless of how the numbers are grouped. This means that changing the grouping of the numbers being multiplied will not change the final product. For example, (2 x 3) x 4 is equal to 2 x (3 x 4), as both expressions yield a product of 24.

How does the associative property affect the grouping of numbers in addition?

The associative property states that when adding three or more numbers, the grouping of the numbers does not change the result. In other words, you can regroup the numbers being added in any way and the answer will remain the same. For example, (2 + 3) + 4 is equal to 2 + (3 + 4) which both equal 9. This property allows us to simplify calculations and rearrange the numbers being added without altering the final sum.

How does the associative property affect the grouping of numbers in multiplication?

The associative property in multiplication allows us to change the grouping of numbers without changing the result. This means that the way in which numbers are grouped together in a multiplication problem does not impact the final product. For example, (2 x 3) x 4 is equal to 2 x (3 x 4), demonstrating the associative property and showing that the result will remain the same regardless of how the numbers are grouped together.

Can the associative property be applied to any set of numbers?

Yes, the associative property can be applied to any set of numbers, as long as the operation being performed is addition or multiplication. The property states that changing the grouping of numbers being added or multiplied will not change the result. This means that regardless of how numbers are grouped together, the final outcome will remain the same.

How does the associative property simplify calculations?

The associative property states that the grouping of numbers in a mathematical operation does not affect the result. This simplifies calculations by allowing us to regroup numbers in a way that is easier to compute mentally or on paper. By rearranging the numbers in an operation, we can choose the grouping that is most convenient for us, making it faster and more efficient to perform calculations.

Why is the associative property useful in algebraic expressions?

The associative property is useful in algebraic expressions because it allows us to group numbers or variables in different ways without changing the result of the operation. This property helps simplify computations and can make calculations easier to evaluate by rearranging terms in a way that is more convenient. By using the associative property, we can combine like terms and perform operations more efficiently.

How is the associative property used to regroup terms in an equation?

The associative property allows for grouping of terms in an equation without changing the result. By regrouping terms using the associative property, we can rearrange the terms in a way that makes it easier to simplify or solve the equation. This property is particularly helpful when dealing with addition or multiplication because it allows for flexibility in how terms are grouped together in an equation while preserving the overall result.

Can the associative property be applied to other mathematical operations, like subtraction or division?

No, the associative property only applies to addition and multiplication, not subtraction or division. The associative property states that changing the grouping of the numbers in an operation does not change the result. For subtraction or division, changing the grouping of numbers would typically result in different outcomes, so the associative property does not hold for these operations.

What are some real-world examples where the associative property is utilized?

The associative property is commonly used in arithmetic operations and mathematical equations. For example, when adding or multiplying a set of numbers, the order in which the numbers are grouped does not affect the outcome. In computer programming, the associative property is used in representing expressions and performing calculations efficiently. It is also used in database queries and operations, where the order of the operations does not impact the final result. Additionally, in fields such as physics and engineering, the associative property is applied in calculations involving complex formulas and equations.