Area of Triangle Worksheets Printable

Triangles are a fundamental shape in geometry, composed of three sides and three angles. Understanding how to find the area of a triangle is an essential skill for those studying math or pursuing a career in architecture, engineering, or design. To help reinforce this concept, printable area of triangle worksheets are available to provide targeted practice and enhance understanding for students at various skill levels.

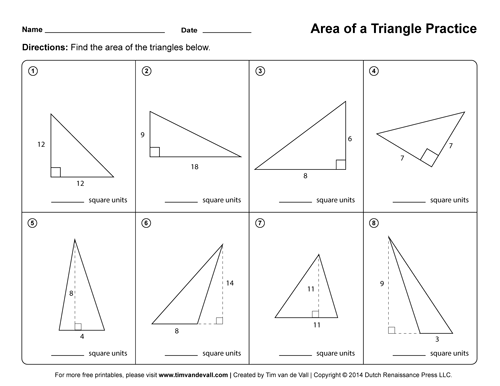
  Triangle Worksheet

---

  7th Grade Area Worksheet Triangle

---

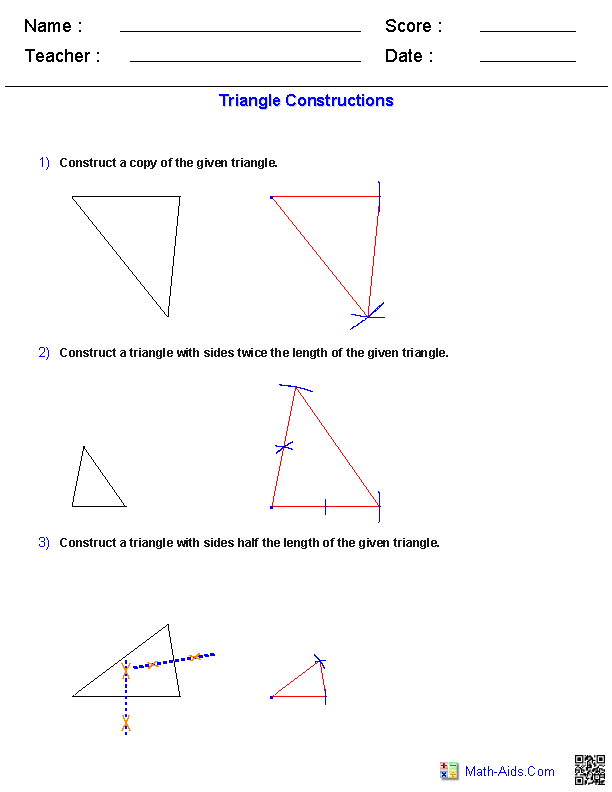
  Math Triangle Constructions Worksheet

---

  Free Printable Triangle Shapes

---

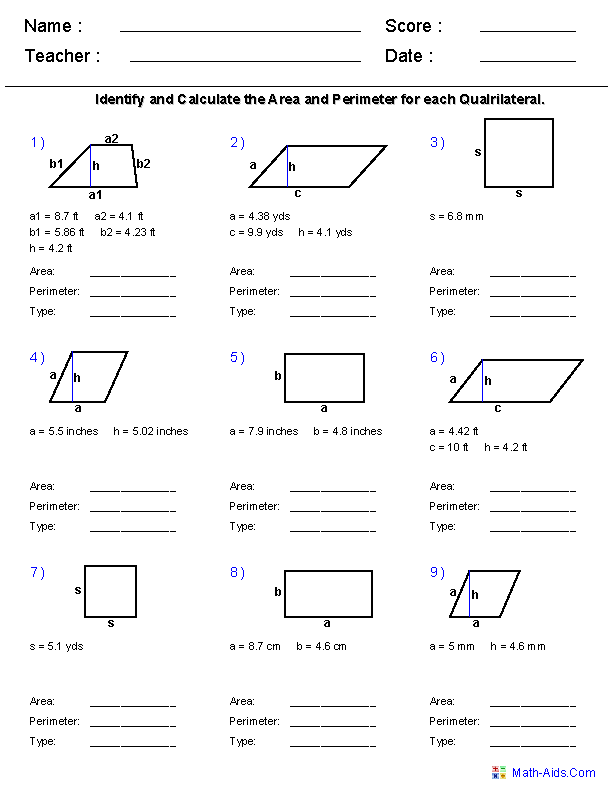
  Area and Perimeter Worksheets 6th Grade

---

  Rectangle Tracing Worksheets Preschool

---

  Area and Perimeter Square Unit Worksheets

---

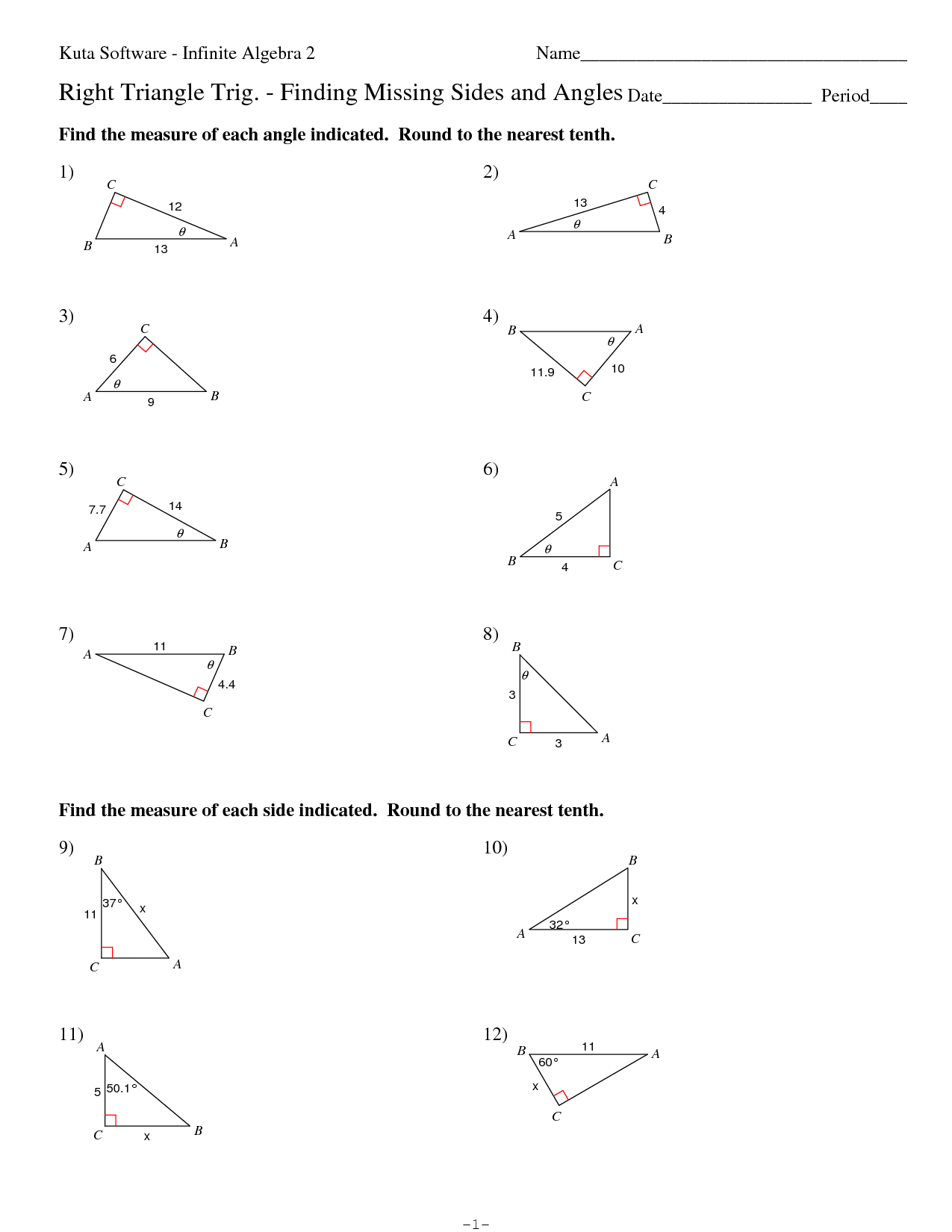
  Right Triangle Trigonometry Worksheet

---

  Maze Shape Triangle Worksheets

---

  5th Grade Multiplication Worksheets

---

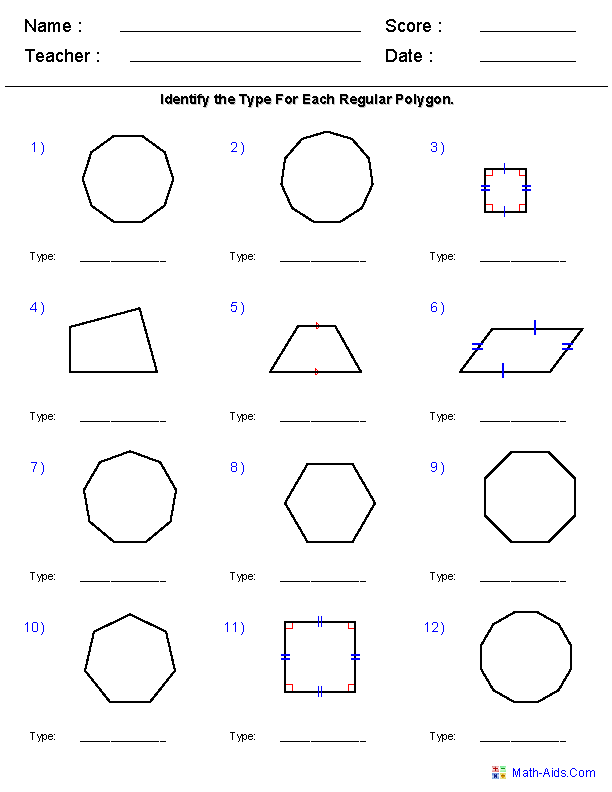
  Polygon Worksheet

---

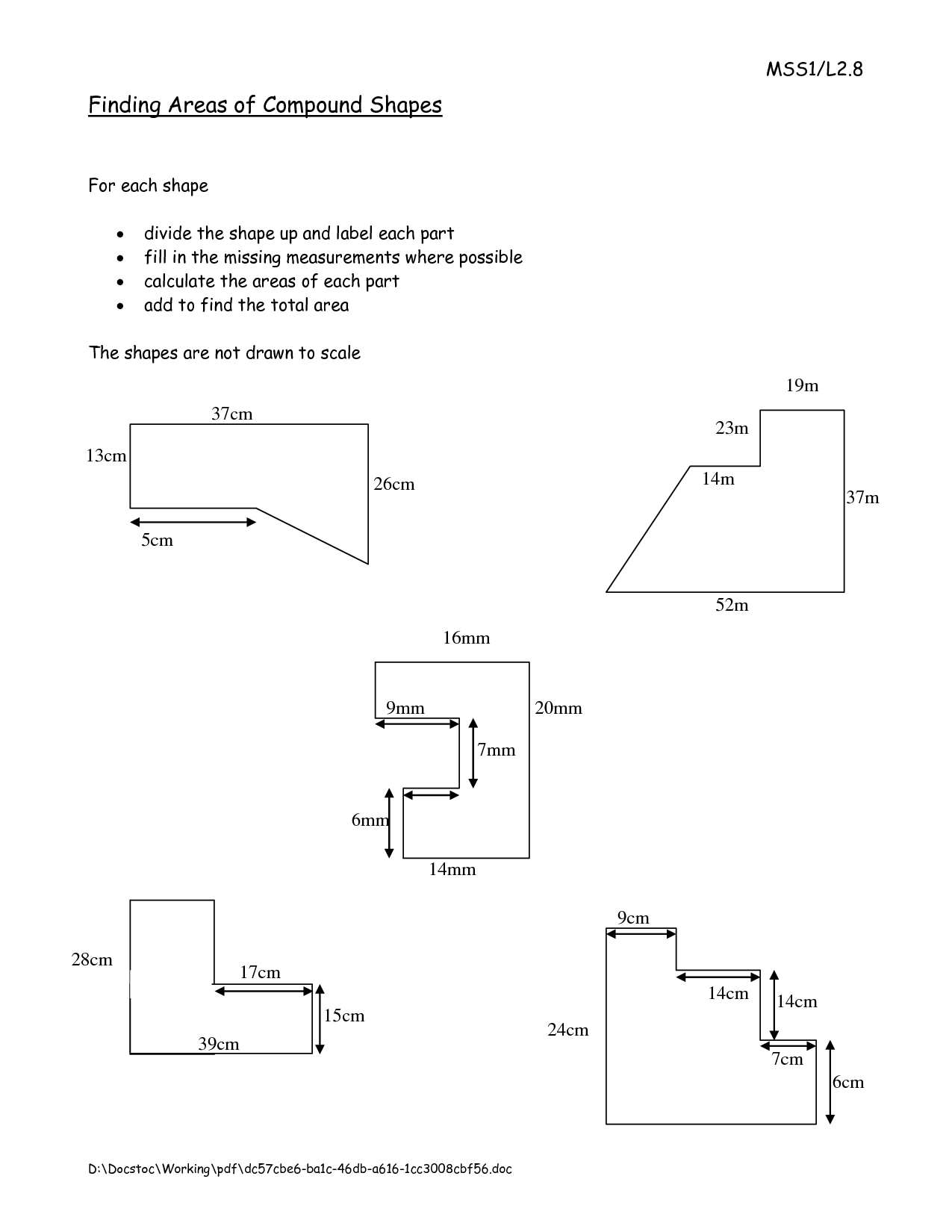
  Compound Shapes Area Worksheet

---

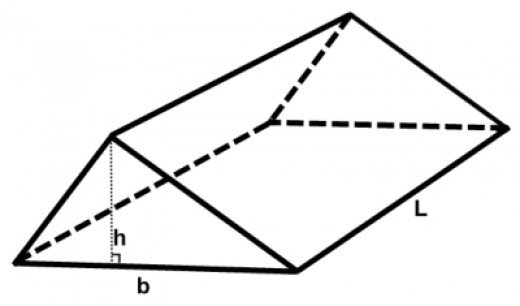
  Triangular Prism

---

  Area Perimeter Word Problem Worksheets

---

  7th Grade Math Vocabulary Words

---

  Free Printable Shape Tracing Worksheets

---

What is the formula for finding the area of a triangle?

The formula for finding the area of a triangle is Area = 1/2 * base * height, where base is the length of the triangle's base and height is the perpendicular distance from the base to the opposite vertex.

How do you calculate the base of a triangle?

To calculate the base of a triangle, you need to know the area of the triangle as well as its height. The formula to find the area of a triangle is 1/2 x base x height. Rearranging this formula, you can solve for the base by dividing the area by the height and then multiplying the result by 2. In other words, base = (2 x area) / height.

Can you use any two sides of a triangle to calculate its area?

No, you cannot calculate the area of a triangle with only two sides. To calculate the area of a triangle, you need both the base and the height. If you have only two sides, you would also need the measure of the angle between those two sides in order to determine the height and then calculate the area using the formula 1/2 x base x height.

What is the significance of using the height of a triangle in the area calculation?

The height of a triangle is used in the area calculation because it provides a perpendicular distance from the base of the triangle to its top vertex, which represents the deepest point of the triangle. This height is crucial in determining the amount of space enclosed within the triangle and is necessary for obtaining an accurate measurement of its area using the formula: Area = 1/2 × base × height.

Are there different methods to calculate the area of a triangle if it is not a right triangle?

Yes, there are different methods to calculate the area of a triangle that is not a right triangle. One common method is using the formula for the area of a triangle, A = ½ * base * height, where the base and height are perpendicular to each other. Another method is using the Heron's formula, which calculates the area based on the lengths of the three sides of the triangle using the semi-perimeter. Additionally, trigonometry can be used to calculate the area if the angles and side lengths of the triangle are known.

How do you find the area of an equilateral triangle?

To find the area of an equilateral triangle, you can use the formula A = (?3/4) * s^2, where s is the length of one side of the triangle. Simply square the length of one side, multiply it by (?3/4), and that will give you the area of the equilateral triangle.

Are there any special cases where finding the area of a triangle is easier?

Yes, finding the area of a triangle is easier when the triangle is a right triangle because we can use the formula Area = 0.5 * base * height, where the base and height are the sides perpendicular to each other. In this case, the base and height are easily identifiable, making calculations simpler compared to other types of triangles where additional formulas or trigonometric functions may be required to determine the area.

How can you use the Pythagorean theorem to find the area of a right triangle?

To find the area of a right triangle using the Pythagorean theorem, you first need to determine the lengths of the two sides that form the right angle (a and b). Once you have those lengths, you can use the formula for the area of a triangle, which is A = 1/2 * base * height. In this case, the base and height would be the two sides that form the right angle. So you can calculate both the base and height using the Pythagorean theorem (c^2 = a^2 + b^2), and then plug those values into the formula for the area to find the area of the right triangle.

Is it possible to find the area of an obtuse triangle?

Yes, it is possible to find the area of an obtuse triangle using the formula A = 0.5 * base * height, where the base is the length of any side of the triangle and the height is the perpendicular distance from that side to the opposite vertex. The height may fall outside the triangle for an obtuse triangle, but you can extend a line from the opposite vertex to create a right triangle where the extended line is the height.

Are there any real-world applications for finding the area of a triangle?

Yes, finding the area of a triangle has several real-world applications. For example, architects and engineers use the area of a triangle to calculate the necessary materials needed for construction projects. In surveying and map-making, the area of triangular plots of land or geographic features can be determined. Additionally, in fields such as science, business, and finance, the area of a triangle can be used in various calculations and analyses.