Adding Polynomials Worksheet Printable
Are you a math teacher or a student looking for a helpful resource to practice adding polynomials? Look no further! We have created a comprehensive and easy-to-use adding polynomials worksheet that is perfect for anyone seeking to master this important mathematical concept.
Table of Images 👆
- Polynomial Practice Worksheets with Answers
- Adding Polynomials Worksheet
- Factoring Polynomials Worksheet
- Adding Polynomials Worksheet
- Algebra Polynomials Worksheets
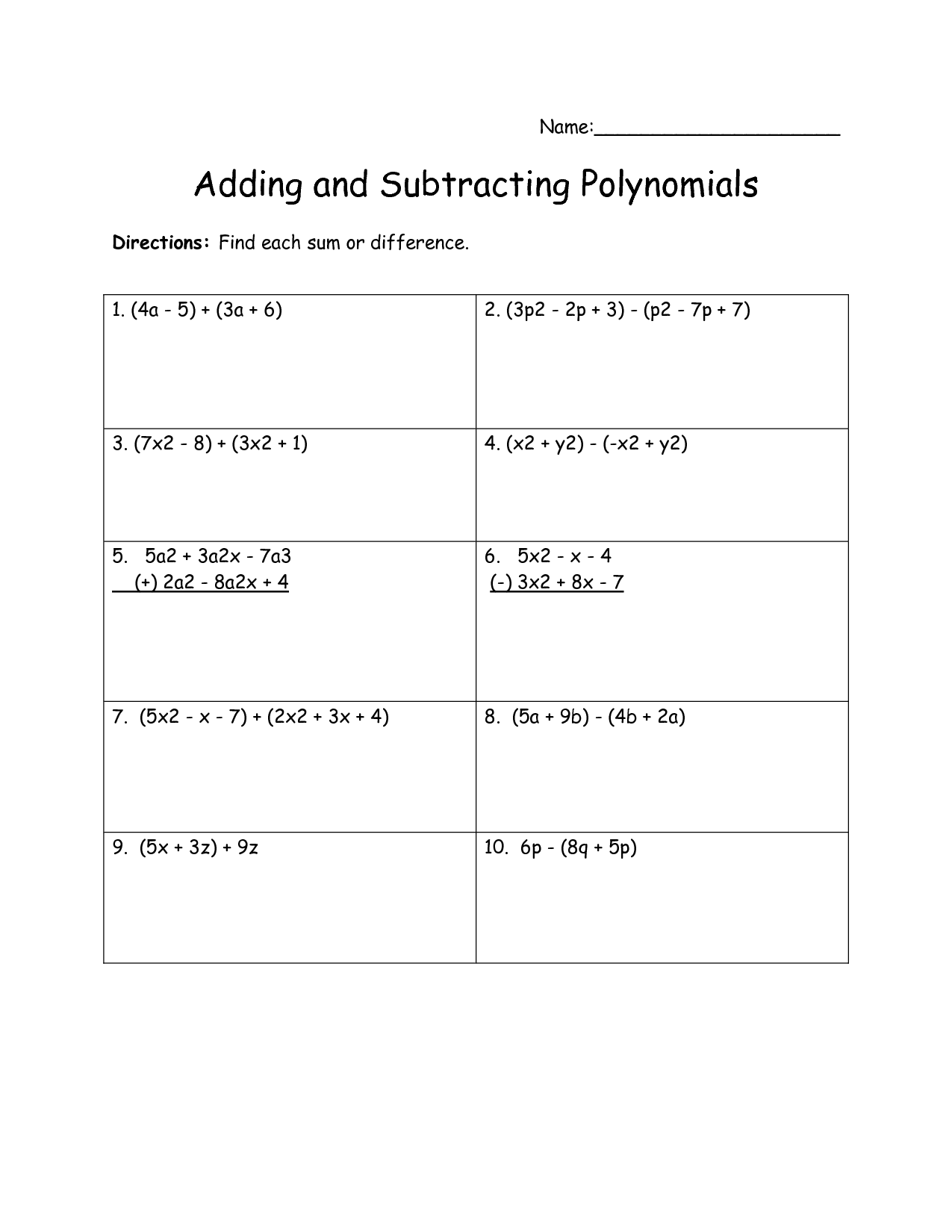
- Adding and Subtracting Polynomials Worksheet Answers
- Multiplying and Factoring Polynomials Worksheet
- Algebra Factoring Polynomials Worksheet
- Subtracting and Adding Linear Expressions Worksheet
- Adding and Subtracting Polynomials Worksheets
- Adding and Subtracting Polynomials Worksheet with Answers
- Multiplication of Exponents and Division Worksheets
- Adding Fractions with Like Denominators Worksheets
- Dividing Fractions and Mixed Numbers Worksheets
- 3rd Grade Math Worksheets Printable
- Factoring by Grouping Worksheet Answers
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is a printable worksheet?
A printable worksheet is a physical or digital document designed for educational or developmental purposes, typically containing questions, exercises, or activities to be completed by students or learners. These worksheets can cover a variety of subjects and topics, providing a structured way for individuals to practice and apply their knowledge or skills.
What is the purpose of adding polynomials in mathematics?
The purpose of adding polynomials in mathematics is to combine like terms and simplify expressions. This process allows us to efficiently perform operations on algebraic expressions, solving equations, and manipulating formulas in various branches of mathematics and real-life applications such as engineering, physics, and economics.
How do you identify like terms in polynomials?
To identify like terms in polynomials, look for terms that have the same variable(s) raised to the same powers. For example, in the polynomial expression 5x^2 + 3x - 2x^2 + 7, the terms 5x^2 and -2x^2 are like terms because they both have the variable x raised to the power of 2. Similarly, 3x and 7 are also like terms because they are both constant terms with no variables. Combine like terms by adding or subtracting their coefficients while keeping the variables and exponents unchanged.
What are the steps involved in adding polynomials?
To add polynomials, you need to first align like terms (terms with the same variable and exponent), then combine those like terms by adding or subtracting their coefficients. Start by adding or subtracting the coefficients of the terms with the highest degree, then continue working downwards until all like terms have been combined. Once all like terms have been added or subtracted, simplify the expression by collecting like terms and arranging them in descending order of degree.
Can you add polynomials with different degrees?
Yes, you can add polynomials with different degrees by aligning like terms and performing the addition operation. To do this, each term of the polynomials is combined based on its degree, and any missing terms are represented as zero in order to accurately add the polynomials together. The resulting sum will typically have a degree equal to the highest degree present in the original polynomials.
What is the degree of a polynomial?
The degree of a polynomial is the highest power of the variable in the polynomial. It is determined by looking at the term with the highest exponent on the variable in the polynomial expression.
How do you simplify the sum of two or more polynomials?
To simplify the sum of two or more polynomials, you combine like terms by adding or subtracting coefficients of terms with the same variable and degree. First, group together like terms, then add or subtract the coefficients. This process simplifies the expression by reducing it to a single polynomial with the combined terms.
What is the difference between adding and subtracting polynomials?
The main difference between adding and subtracting polynomials is the operation being performed. When adding polynomials, you combine like terms by adding their coefficients together. In contrast, when subtracting polynomials, you combine like terms by subtracting their coefficients. The key is to pay attention to the signs of the terms and ensure they are handled correctly when performing the subtraction operation.
Can you add polynomials with different numbers of terms?
Yes, you can add polynomials with different numbers of terms by grouping like terms together. Combine terms that have the same variable and exponent to simplify the expression. Terms without matching variables can be kept separate when adding or subtracting polynomials with different numbers of terms.
Can you provide an example of adding polynomials using a printable worksheet?
I'm unable to provide a printable worksheet directly, but here's an example of adding polynomials: (3x^2 + 2x + 5) + (2x^2 - 4x + 3). Line up like terms and add coefficients: (3x^2 + 2x + 5) + (2x^2 - 4x + 3) = (3x^2 + 2x^2) + (2x - 4x) + (5 + 3) = 5x^2 - 2x + 8. You can create your own printable worksheet by writing down similar problems on a piece of paper or using a word processor or spreadsheet software.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.





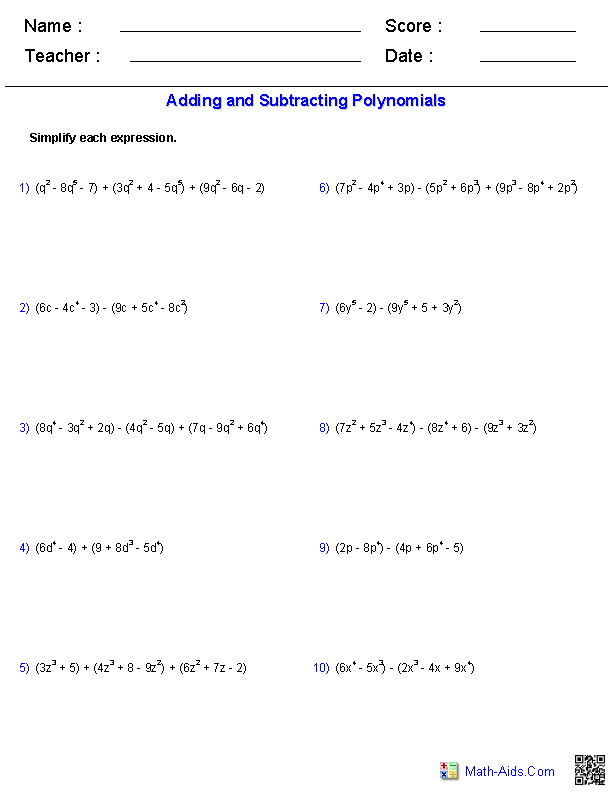





















Comments