A Circle of Radius and Diameter Worksheets

If you're a math teacher looking for a reliable resource to help your students practice their skills with radius and diameter, you've come to the right place. In this blog post, we will introduce a collection of well-crafted worksheets that focus specifically on these key geometric concepts.

  Geometry Circle Worksheets

---

  Geometry Circle Worksheets

---

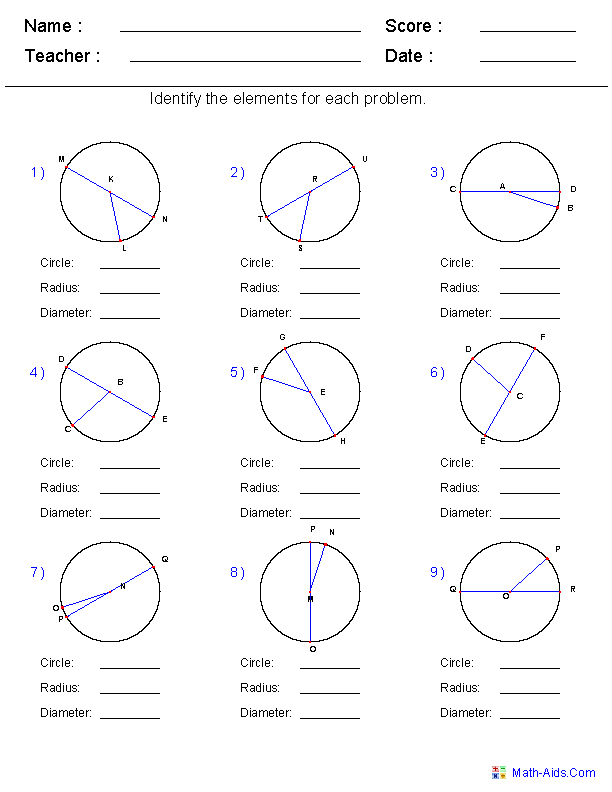
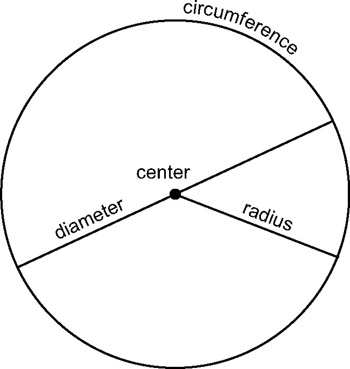
  Circle Parts Worksheet

---

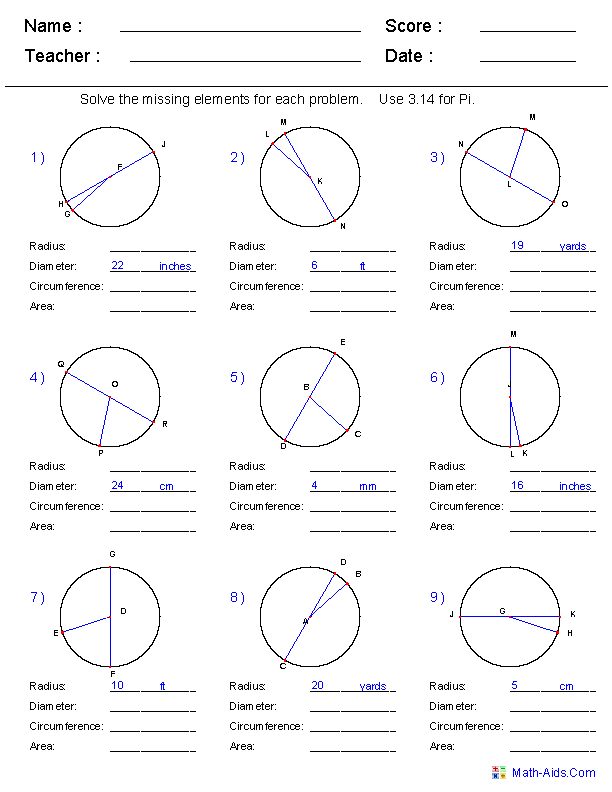
  Area Circumference Circle Worksheet

---

  Radius and Diameter of a Circle Worksheets

---

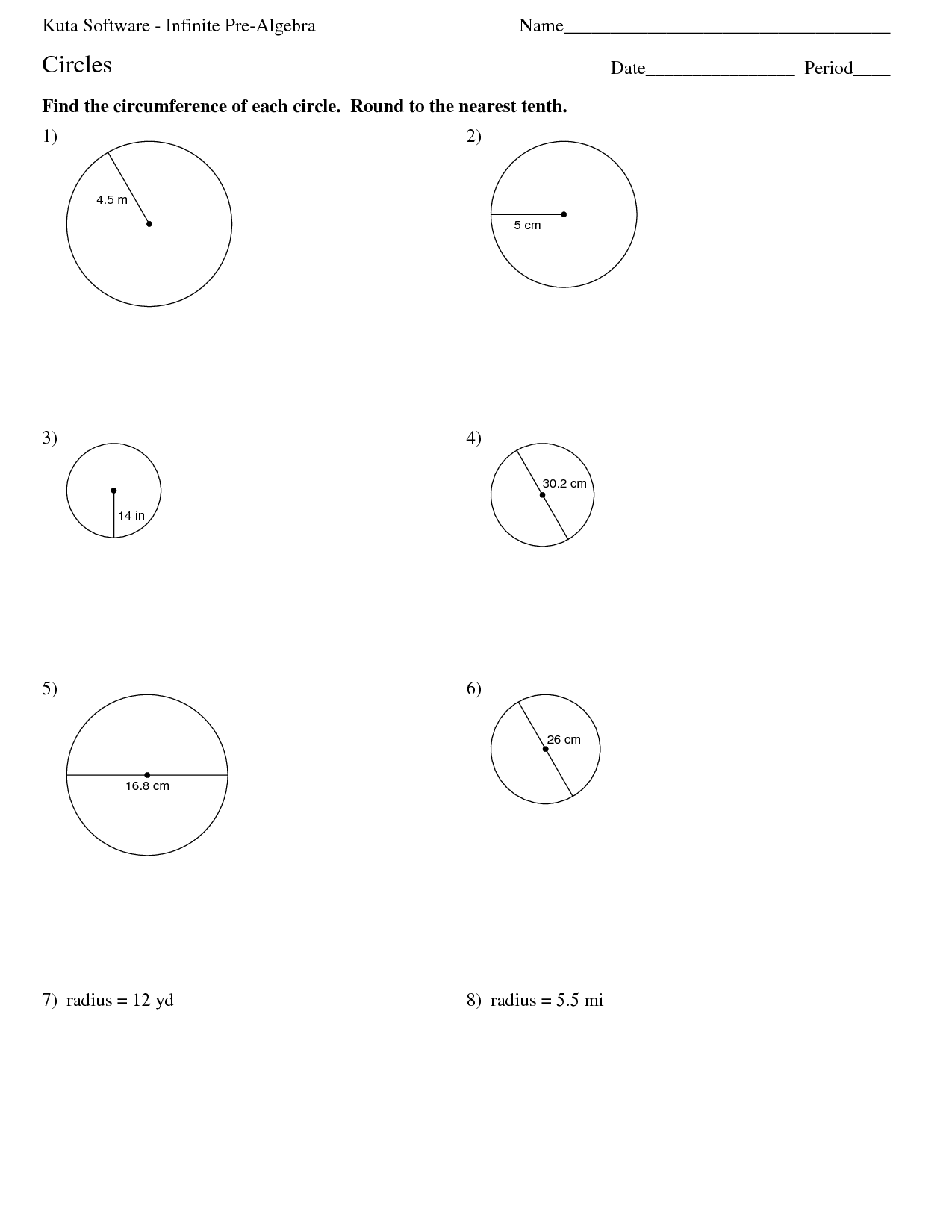
  Radius Diameter Circumference

---

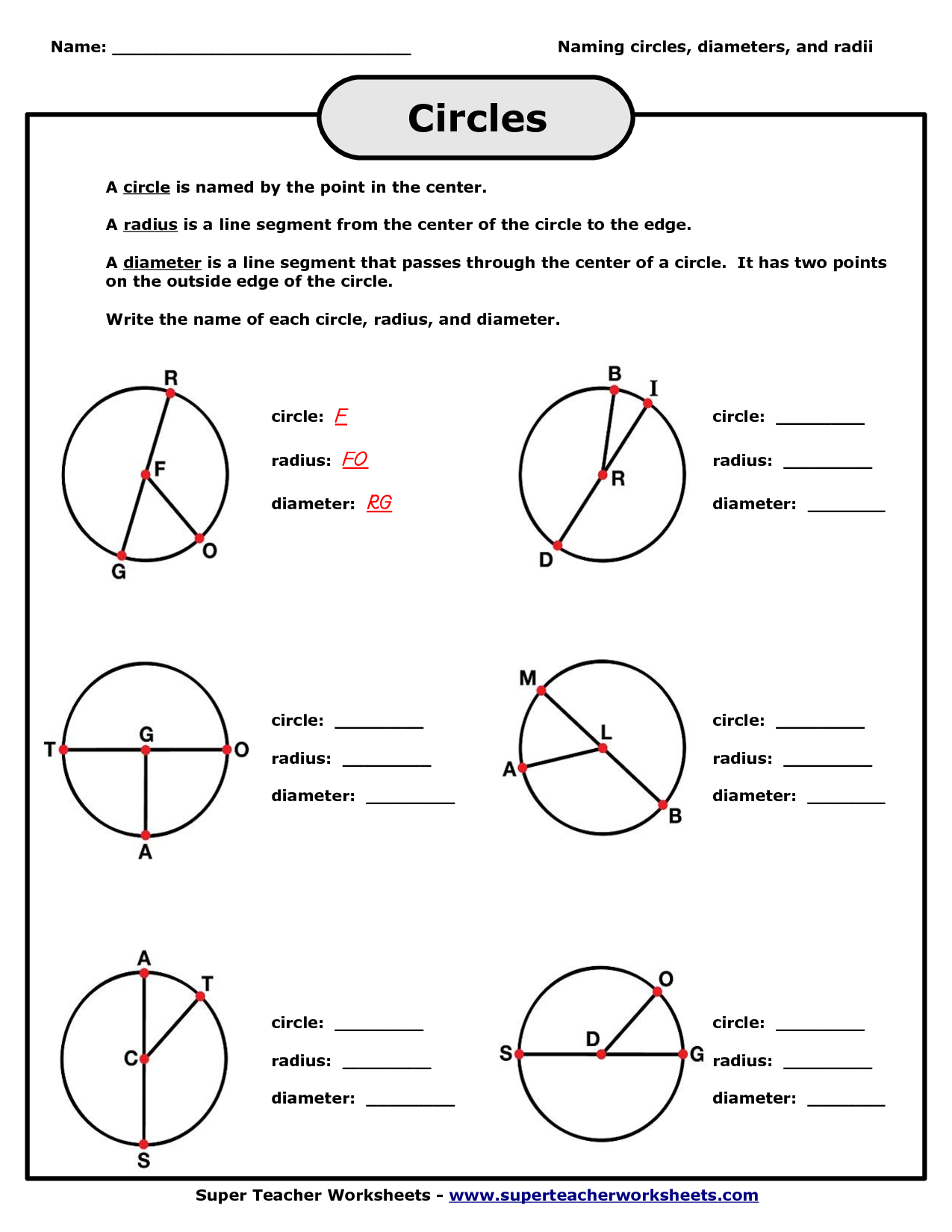
  Circle Radius and Diameter Worksheets

---

  Radius Diameter Circumference

---

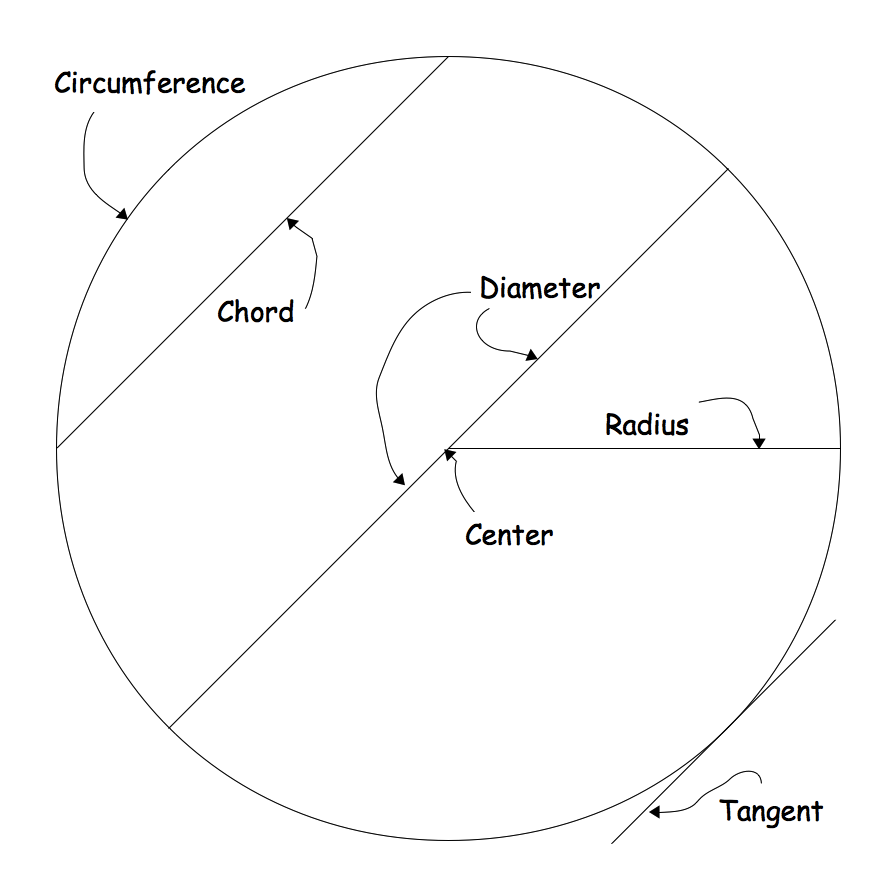
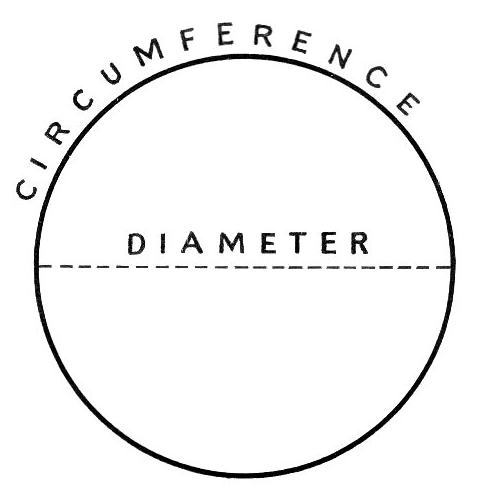
  Circumference Circle Diagram

---

  Circle Radius Circumference

---

  Circle with Diameter and Radius

---

What is the formula for the circumference of a circle?

The formula for the circumference of a circle is C = 2?r, where C represents the circumference and r is the radius of the circle.

What is the definition of radius?

The radius of a circle is the distance from the center of the circle to any point on the circle's circumference. It is a straight line segment that connects the center to the outer edge of a circle, and is always equal in length to the radius at any point on the circle.

How is the diameter of a circle related to its radius?

The diameter of a circle is two times the length of its radius. In other words, the radius is half the length of the diameter. This means that the radius and diameter of a circle are directly related, with the diameter being double the length of the radius.

How do you calculate the area of a circle?

To calculate the area of a circle, you use the formula A = ?r^2, where A is the area, ? is a constant approximately equal to 3.14, and r is the radius of the circle. Simply square the radius (multiply it by itself) and then multiply by ? to find the area of the circle.

How does the circumference of a circle compare to its diameter?

The circumference of a circle is always approximately 3.14 times longer than its diameter. This constant ratio is known as pi (?) and is used to calculate the circumference of a circle with the formula C = ?d, where C is the circumference and d is the diameter.

What are some real-life examples of objects that can be modeled as circles?

Some real-life examples of objects that can be modeled as circles include wheels of vehicles such as cars, bicycles, and trucks, coins, lids of jars or containers, plates, CDs or DVDs, hula hoops, steering wheels, clocks, hubcaps, and certain types of buttons. These objects exhibit circular shapes and can be mathematically described and understood using properties and equations related to circles.

How do you find the radius of a circle if you know its diameter?

To find the radius of a circle when you know its diameter, you simply divide the diameter by 2. The radius is always half of the diameter in a circle, so by dividing the diameter in half, you can find the radius of the circle.

How can you determine the diameter of a circle if you only know its radius?

To determine the diameter of a circle when you only know its radius, you simply double the radius value. Since the diameter is twice the length of the radius, multiplying the radius by 2 gives you the diameter of the circle.

What is the relationship between the radius and diameter of a circle?

The radius of a circle is half the length of the diameter. In other words, the diameter of a circle is always twice the length of the radius. This means that if you know the radius of a circle, you can easily find the diameter by multiplying the radius by 2, and if you know the diameter, you can find the radius by dividing the diameter by 2.

How can you use the radius and diameter of a circle to solve geometry problems?

You can use the radius and diameter of a circle to calculate various geometric properties such as the circumference, area, and sector area of the circle. The radius is half of the diameter, so by knowing one value, you can calculate the other. You can use the formula C = 2?r to find the circumference, A = ?r^2 to find the area, and sector area = (?/360)?r^2 to find the area of a sector with a central angle of ? degrees. By understanding the relationship between the radius and diameter, you can efficiently solve geometry problems involving circles.