Which Are Similar Triangles Worksheet

Are you a math teacher searching for a helpful resource to teach your students about similar triangles? Look no further! In this blog post, we will introduce you to various worksheets focused on similar triangles, which are ideal for middle and high school students. Worksheets serve as a valuable tool for reinforcing concepts, providing practice problems, and promoting a better understanding of the subject matter. Let's explore some excellent options to enhance your students' learning experience.

  Right Triangle Pythagorean Theorem Worksheets

---

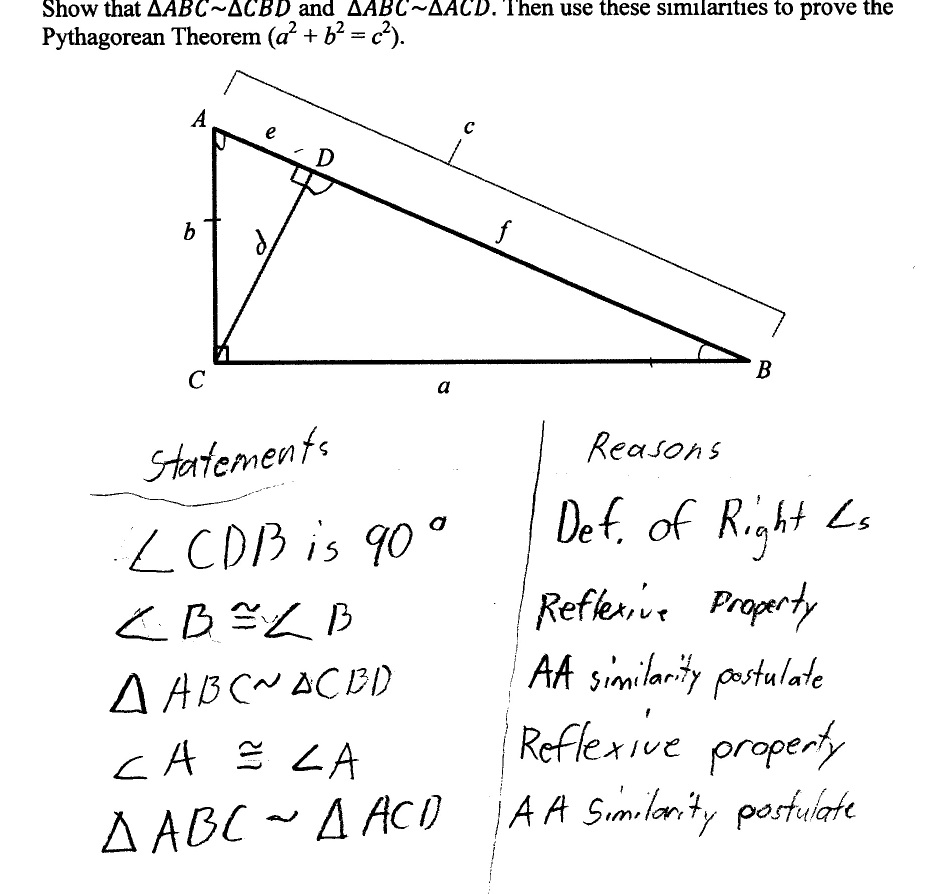
  Pythagorean Theorem Proof

---

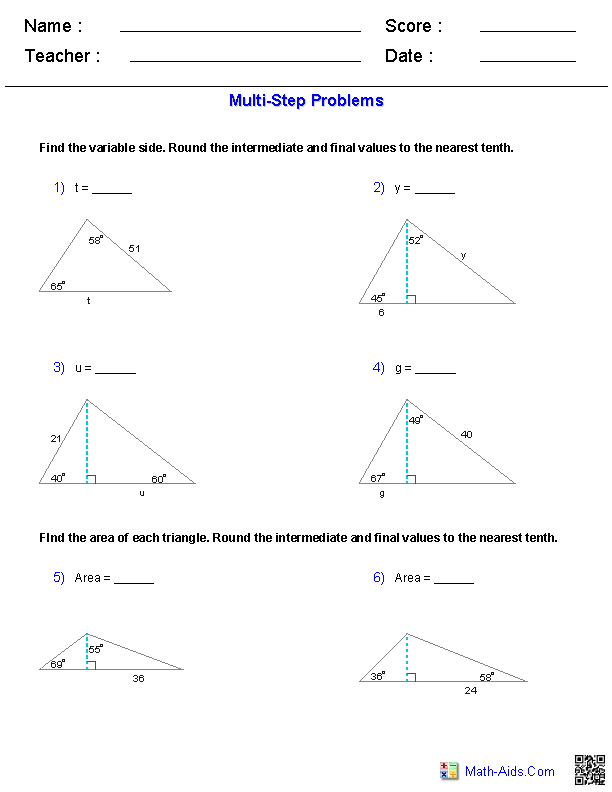
  Solving Right Triangle Trigonometry Worksheet

---

  Similar Figures 7th Grade Worksheets

---

  Similar Triangles Worksheet

---

  Right Triangle Similarity

---

  Drawing Angles Worksheet

---

  Trigonometry Word Problems Worksheet

---

  Special Right Triangles Worksheet

---

  Basic Trigonometry Worksheet

---

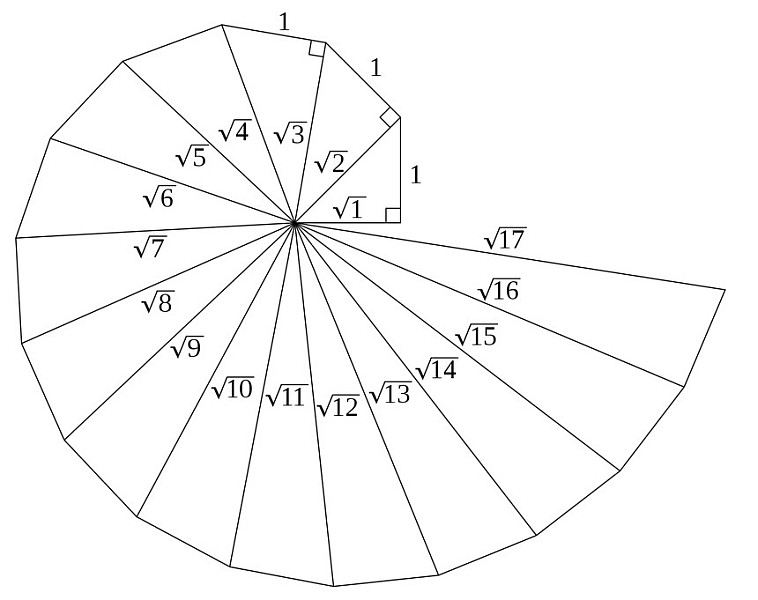
  Spiral of Theodorus Wheel

---

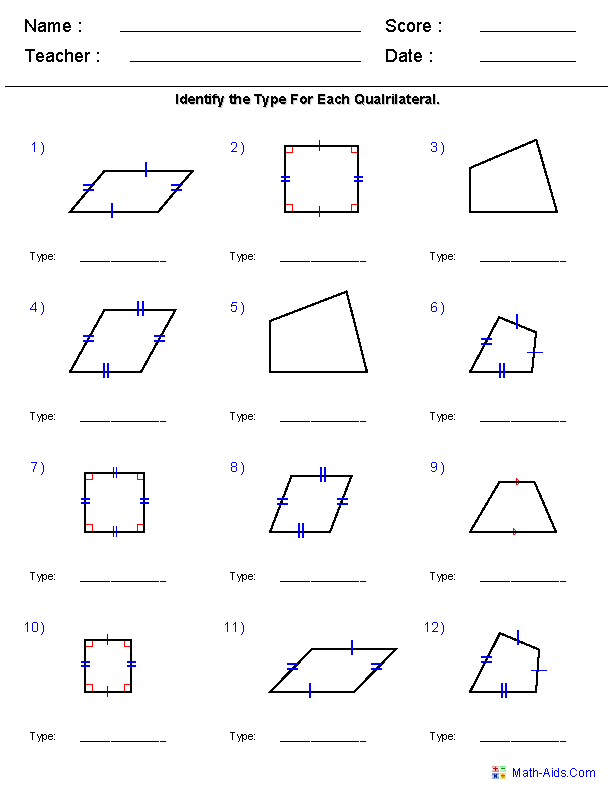
  Types of Quadrilaterals Worksheet

---

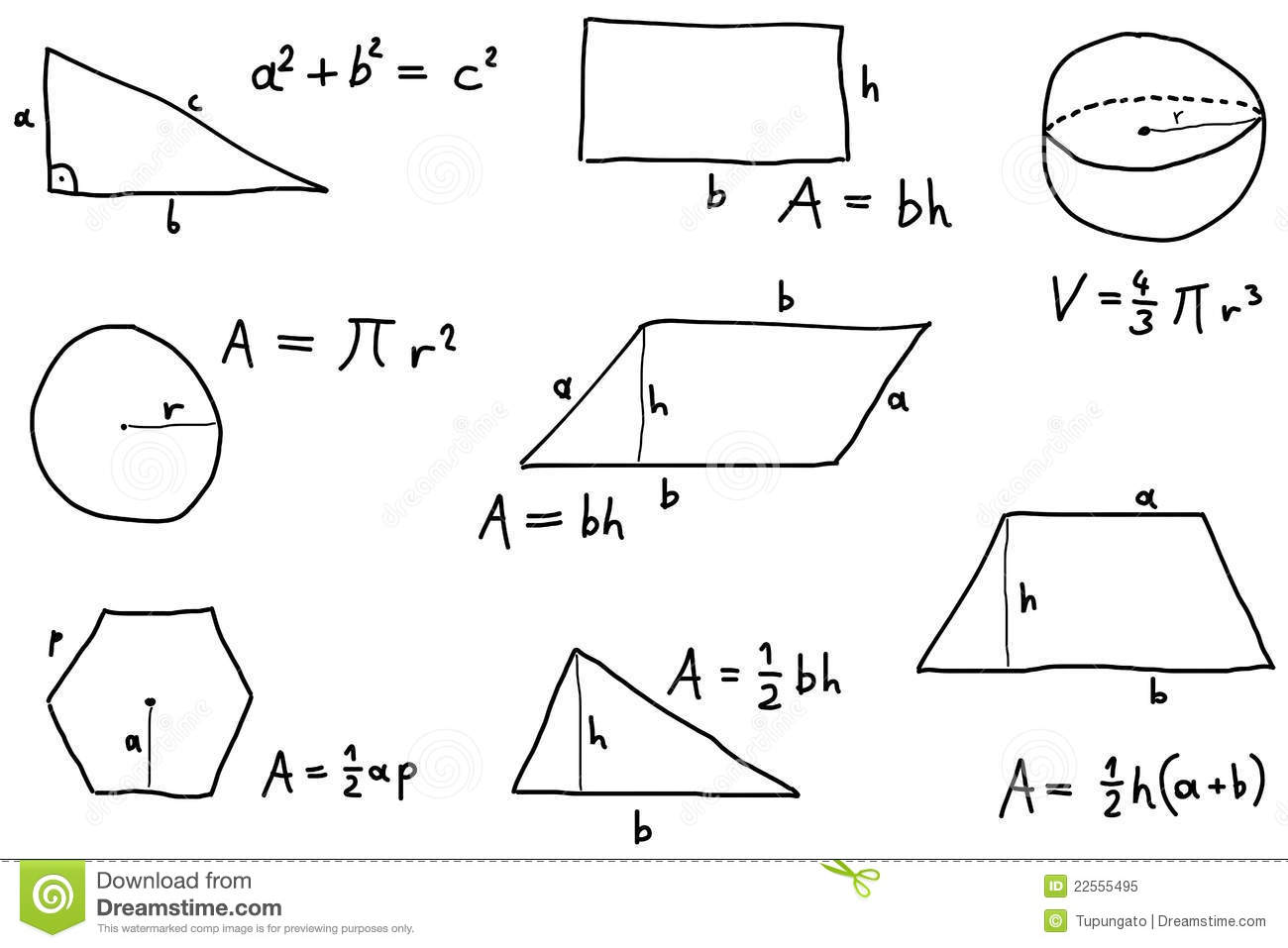
  Math Formulas Geometry Polygon

---

What is the purpose of a Which Are Similar Triangles Worksheet?

The purpose of a Which Are Similar Triangles Worksheet is to help students practice identifying and working with similar triangles, which have the same shape but different sizes. This worksheet can help students develop their understanding of similar triangles, as well as their skills in solving problems involving proportions and ratios within triangles with geometrical relationships.

How do you determine if two triangles are similar?

Two triangles are similar if their corresponding angles are congruent and their corresponding sides are in proportional lengths. This can be determined by checking if all corresponding angles are equal in measure and if the ratios of the lengths of corresponding sides are equal.

What criteria must be met for triangles to be considered similar?

For triangles to be considered similar, two criteria must be met: first, the corresponding angles of the triangles must be congruent, meaning they have the same measure; second, the corresponding sides of the triangles must be proportional, meaning the ratio of the lengths of corresponding sides must be the same for all pairs of sides.

What geometric properties are used to identify similar triangles?

Similar triangles have the same shape but are of different sizes. The key geometric properties used to identify similar triangles are angles and side lengths. If the corresponding angles of two triangles are congruent and the ratios of the corresponding side lengths are equal, then the triangles are considered similar. This is known as the Angle-Angle (AA) similarity criterion and the Side-Side-Side (SSS) similarity criterion. These properties are essential for identifying similar triangles in geometry.

How can you use proportions to solve problems involving similar triangles?

To solve problems involving similar triangles using proportions, you can set up ratios of corresponding sides of the triangles. By comparing the lengths of corresponding sides of similar triangles, you can create proportional relationships. This allows you to set up a proportion with the known sides and find the unknown sides by cross-multiplying. By using the properties of similar triangles and ratios of corresponding sides, you can easily determine the missing lengths in similar triangle problems.

What is the importance of corresponding angles in similar triangles?

Corresponding angles in similar triangles are important because they are congruent, meaning they have the same measure. This property allows us to establish relationships between the sides and angles of similar triangles. By knowing that corresponding angles are equal in similar triangles, we can use this information to solve for missing angles and sides, making calculations easier and more efficient in geometry problems involving similar triangles.

How does the ratio of corresponding sides help identify similar triangles?

The ratio of corresponding sides in similar triangles is constant and equal to each other. By comparing the ratios of the corresponding sides of two triangles, if all ratios are equal, then the triangles are similar. This similarity property helps in identifying similar triangles once the ratios are determined to be equal.

What are some real-life examples of similar triangles?

A real-life example of similar triangles is found in architecture and construction where buildings and structures are designed using scaled models. Another example is map-making, where maps are created using scale measurements to accurately represent the geographical features of a region. Additionally, similar triangles are used in photography for perspective and depth calculations, as well as in engineering applications such as determining heights of tall structures using shadows and angles.

How can you use similar triangles to find the height of an inaccessible object?

To use similar triangles to find the height of an inaccessible object, you can measure the shadows cast by both the object and a known height object when placed under the same light source at the same time. By setting up a proportion between the lengths of the shadows and the heights of the objects, you can create similar triangles. By solving for the height of the inaccessible object using the ratios of the corresponding sides of the similar triangles, you can determine its height accurately.

What is the relationship between the areas of similar triangles?

The relationship between the areas of similar triangles is that the ratio of the areas is equal to the square of the ratio of their corresponding side lengths. In other words, if two triangles are similar, then the ratio of their areas is equal to the square of the ratio of any corresponding side lengths.