Volume of Prisms Worksheet.pdf

Are you in need of a comprehensive worksheet to help your students practice calculating the volume of prisms? Look no further! This Volume of Prisms Worksheet is designed to assist middle school or high school students in mastering this mathematical concept. With a variety of questions that cover different prism shapes and sizes, this worksheet offers plenty of opportunities for your students to strengthen their understanding of finding the volume of prisms.

  Triangular Prism Surface Area Worksheet

---

  Triangular Prism Surface Area Worksheet

---

  7th Grade Math Worksheets

---

  Rectangular Prism Surface Area Worksheet

---

  Rectangular Prism Surface Area Worksheet

---

What is volume?

Volume is the quantity of three-dimensional space enclosed by an object or container. It is measured in cubic units, such as cubic meters or cubic feet, and is calculated by multiplying the length, width, and height of an object. Volume represents how much space an object occupies and is an important concept in various fields such as physics, engineering, and mathematics.

What is a prism?

A prism is a geometric shape that has at least two parallel faces called bases, which are identical polygons, and lateral faces that are parallelograms. It is a three-dimensional object with a constant cross-section along its length, and light passing through a prism can be refracted or separated into its component colors due to the prism's ability to bend light.

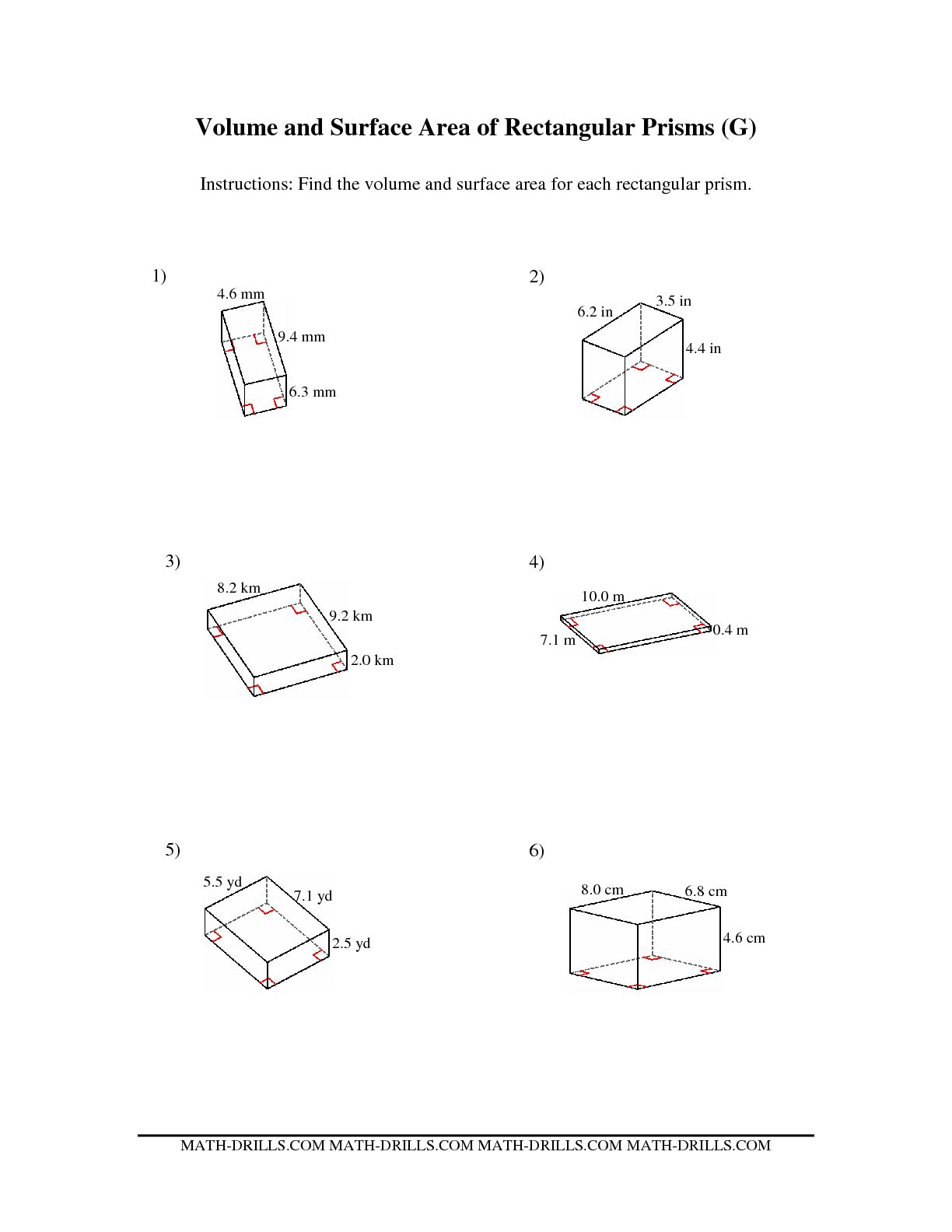
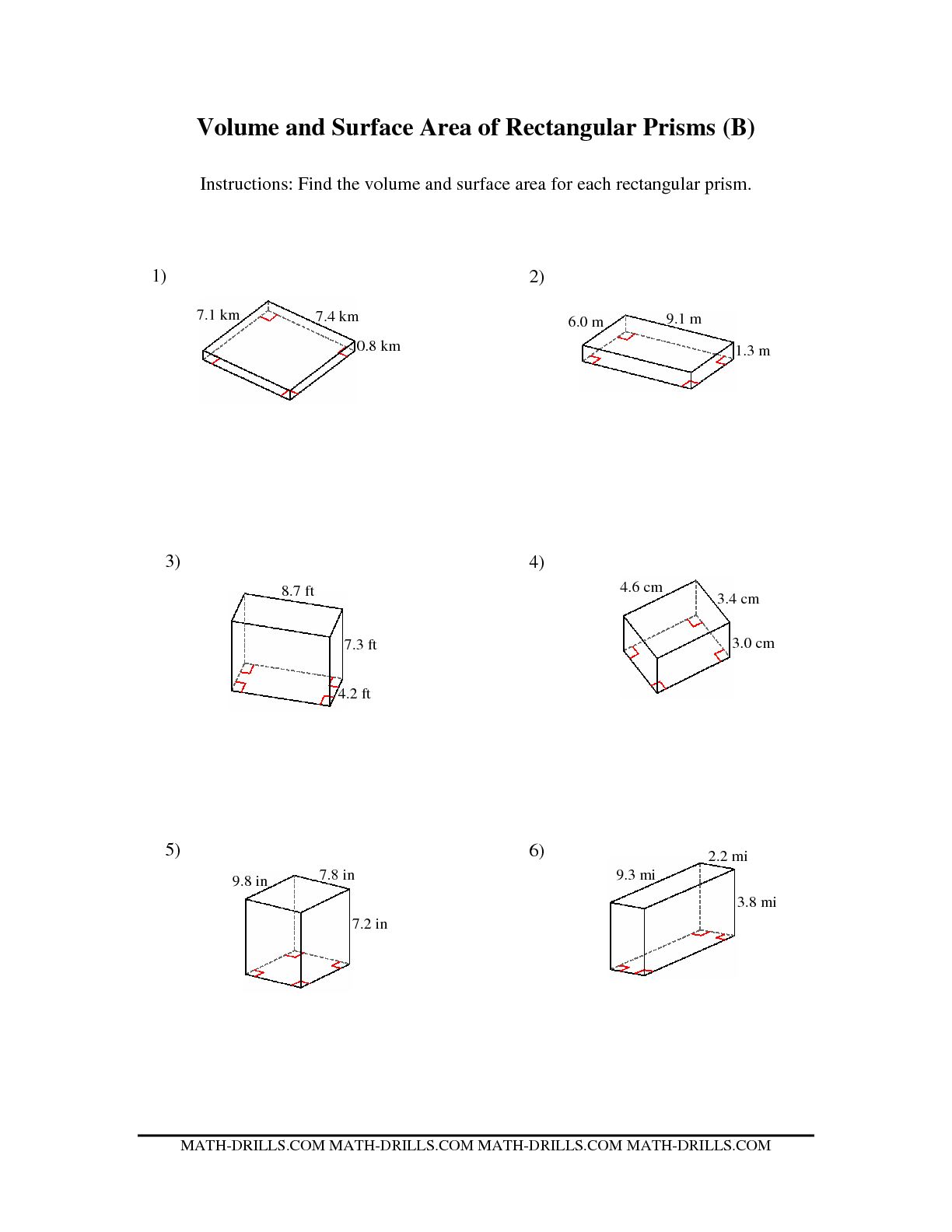
How is the volume of a rectangular prism calculated?

The volume of a rectangular prism is calculated by multiplying the length, width, and height of the prism together. The formula for finding the volume of a rectangular prism is Volume = length x width x height.

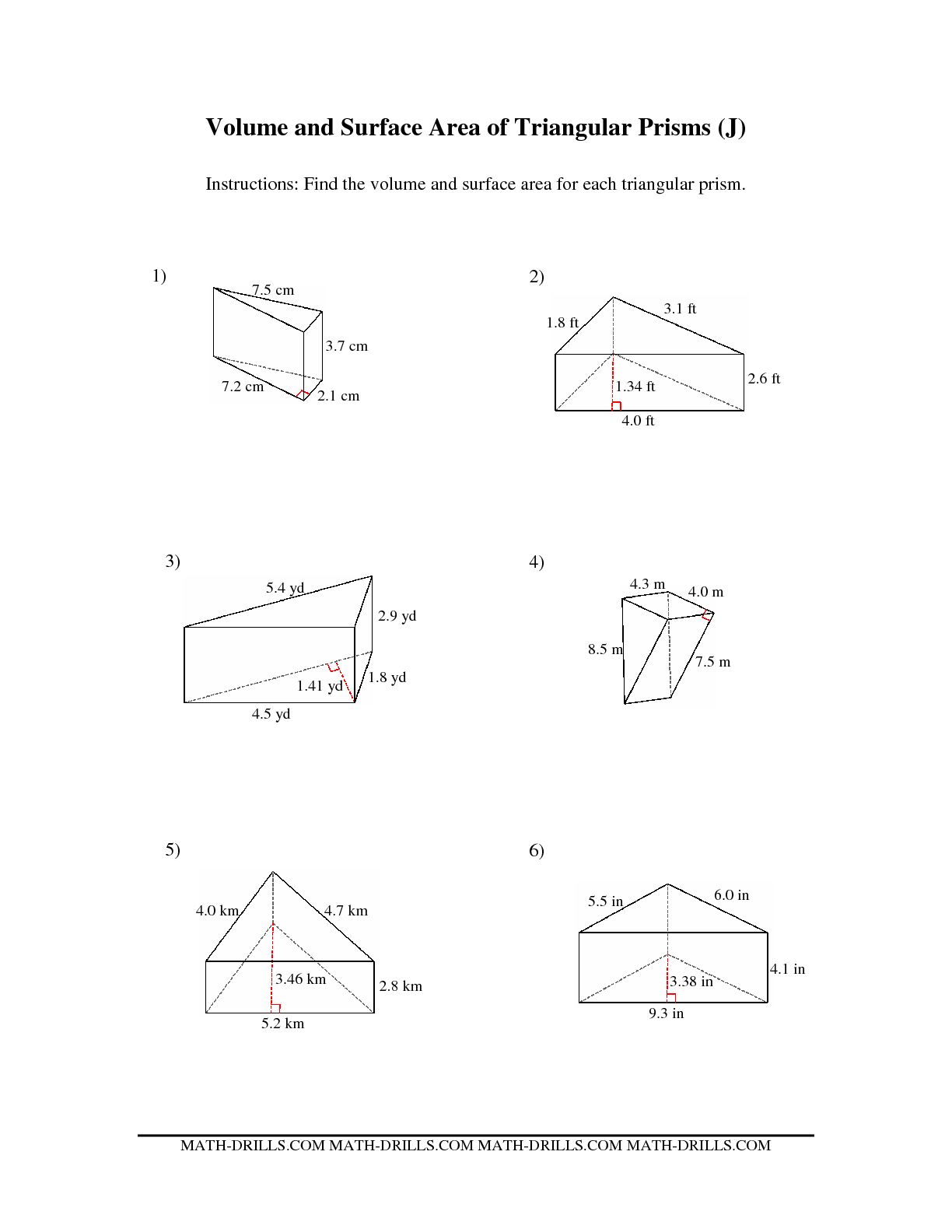
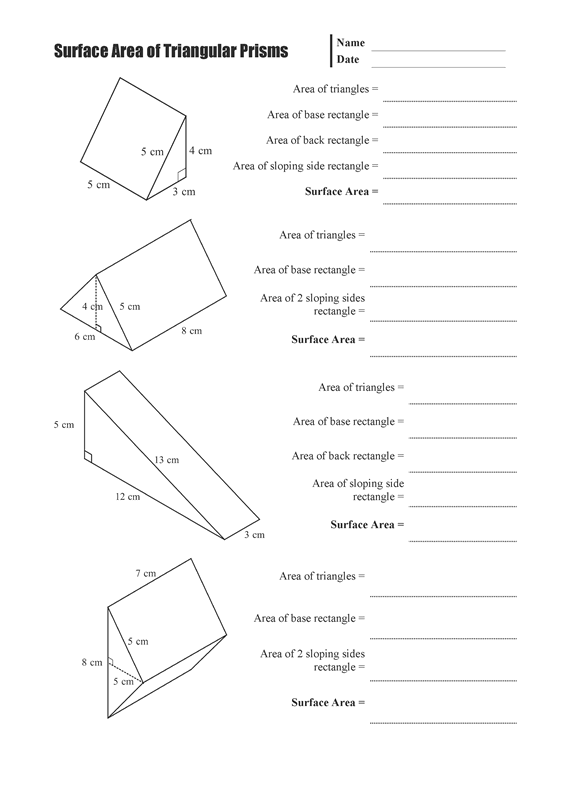
How can the volume of a triangular prism be calculated?

The volume of a triangular prism can be calculated by multiplying the area of the triangular base by the height of the prism. To find the area of the triangular base, calculate half of the base times the height of the triangle. Then, multiply this area by the height of the prism to determine the final volume. The formula is given by V = (1/2) * b * h * H, where V is the volume, b is the base of the triangle, h is the height of the triangle, and H is the height of the prism.

How is the volume of a pentagonal prism determined?

The volume of a pentagonal prism can be determined by multiplying the area of the pentagon base by the height of the prism. The formula for finding the volume of a prism is V = Bh, where B is the area of the base and h is the height of the prism. For a pentagonal prism, you would calculate the area of the pentagon base using the appropriate formula for that shape, and then multiply the result by the height of the prism to find the volume.

What is the formula for finding the volume of a hexagonal prism?

The formula for finding the volume of a hexagonal prism is V = (3?3)/2 × a^2 × h, where 'a' represents the length of one side of the base hexagon and 'h' represents the height of the prism.

What is the volume of a cube?

The volume of a cube is calculated by cubing the length of one of its sides. Hence, the formula for the volume of a cube is V = s^3, where V is the volume and s is the length of a side.

How can the volume of a cylinder be calculated?

The volume of a cylinder can be calculated by multiplying the area of the circular base (?r^2) by the height (h) of the cylinder. The formula for calculating the volume of a cylinder is V = ?r^2h, where r is the radius of the base of the cylinder and h is the height of the cylinder.

What is the formula for calculating the volume of a cone?

The formula for calculating the volume of a cone is V = (1/3)?r²h, where V represents the volume, r is the radius of the base of the cone, and h is the height of the cone.

How is the volume of a pyramid determined?

The volume of a pyramid is determined by the formula V = (1/3) * B * h, where V is the volume, B is the area of the base of the pyramid, and h is the height of the pyramid measured perpendicular to the base. This formula can be applied to various types of pyramids, including square-based, triangular-based, or any other polygon-based pyramids.