Vertical Supplementary Complementary Angles Worksheet
If you're a math teacher searching for a valuable resource to help your students practice identifying vertical supplementary and complementary angles, you're in luck. This vertical supplementary and complementary angles worksheet provides a variety of practical exercises that will engage your students while reinforcing this important mathematical concept.
Table of Images 👆
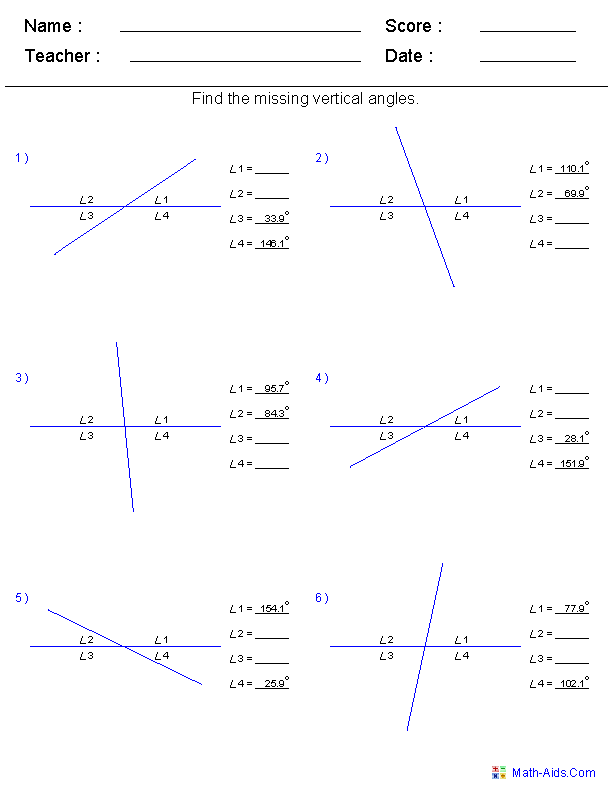
- Vertical and Adjacent Angles Worksheet
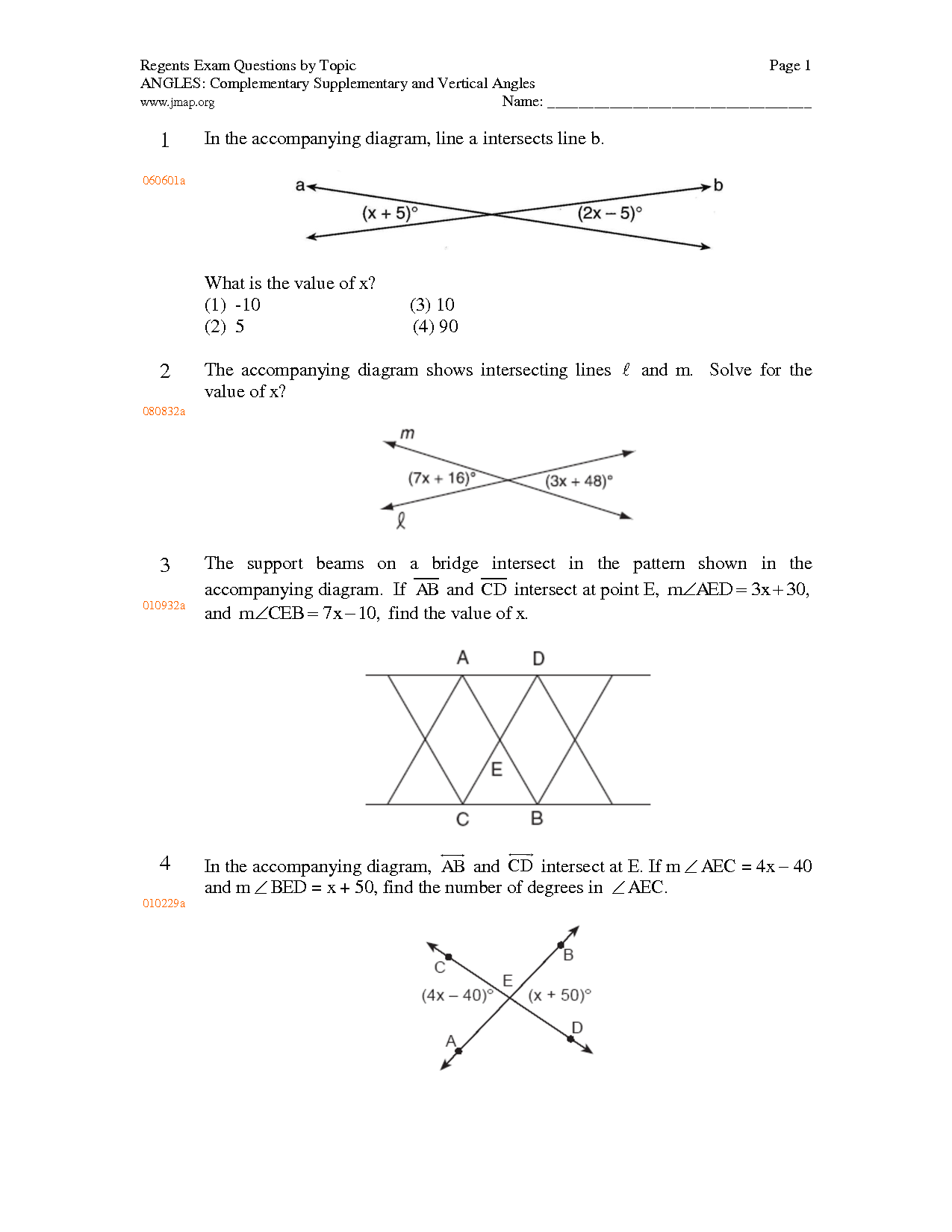
- Vertical Supplementary and Complementary Angle Worksheet
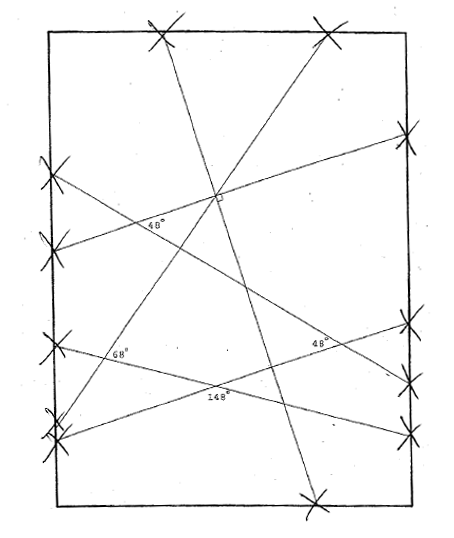
- Complementary Supplementary Angles Worksheet
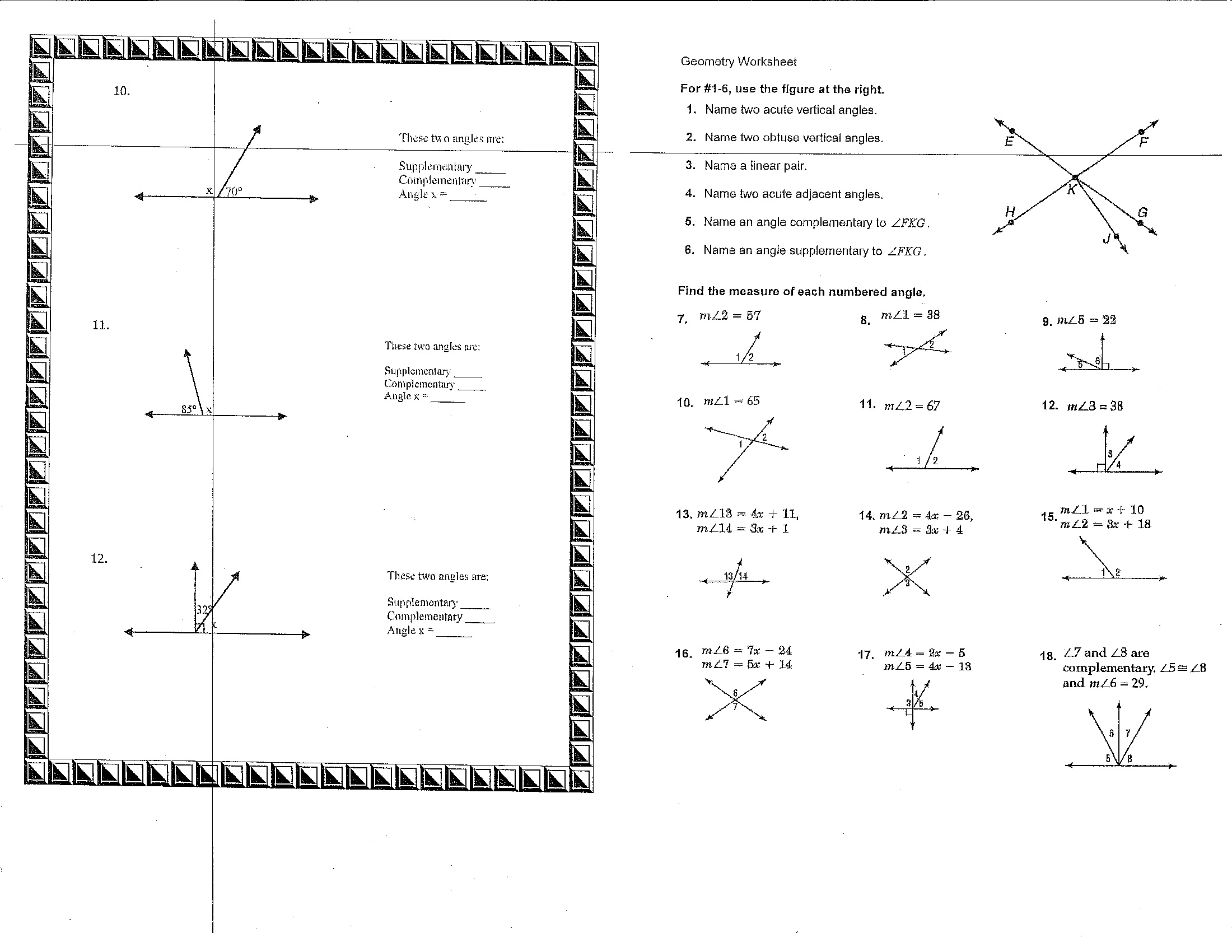
- 8th Grade Math Angles Worksheet
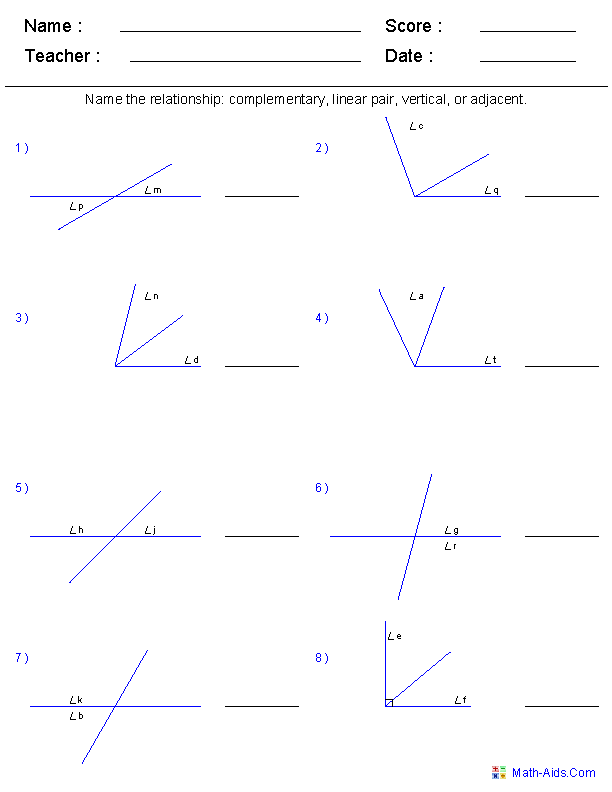
- Angle Pair Relationships Worksheet
- Intersecting Lines Examples
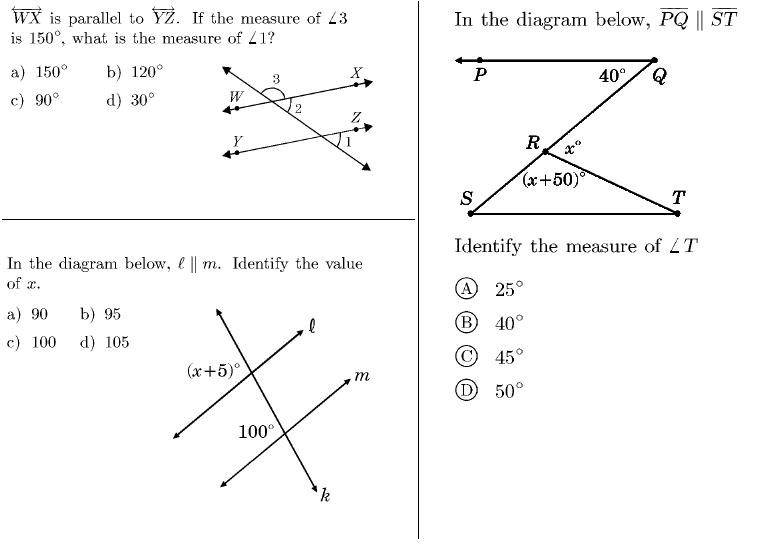
- Angle Parallel Lines and Transversals Worksheet
- Complementary Angles
- Acute Obtuse Right Angles Worksheet
- Gear Machine Diagram
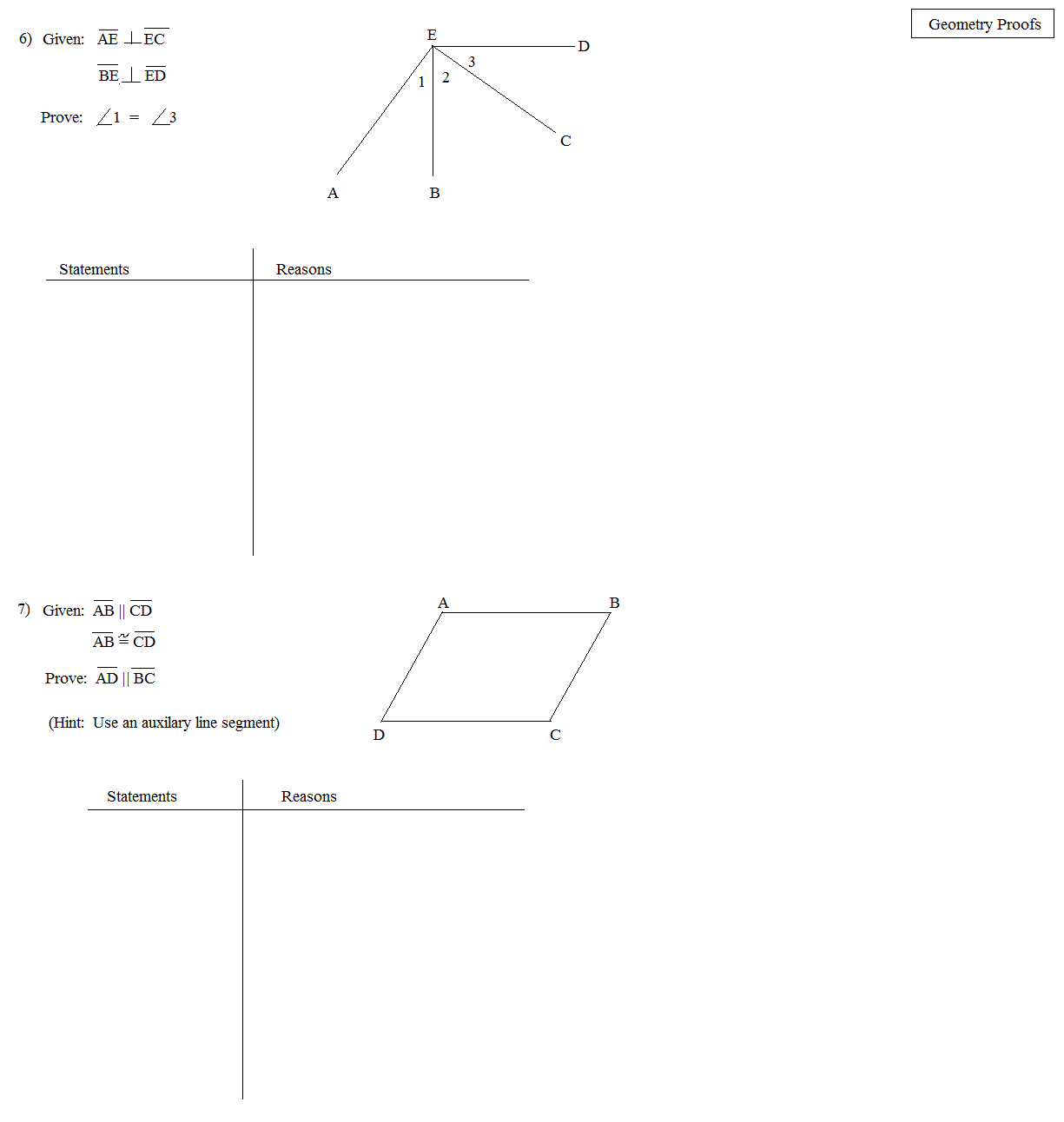
- Geometry Triangle Proofs Worksheet
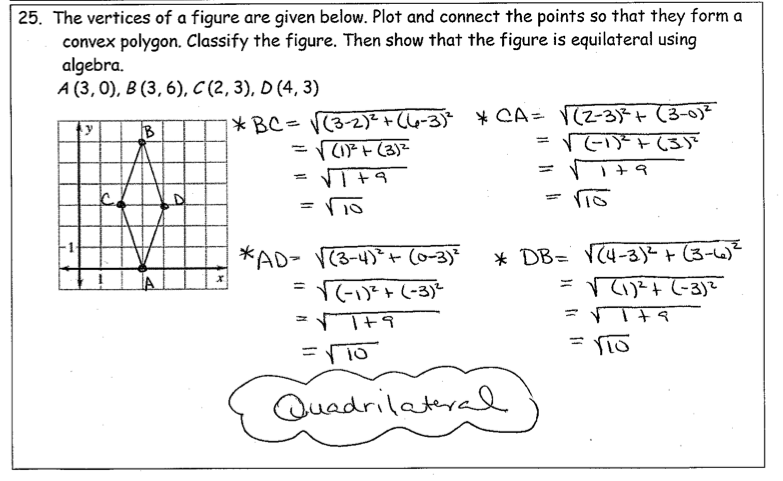
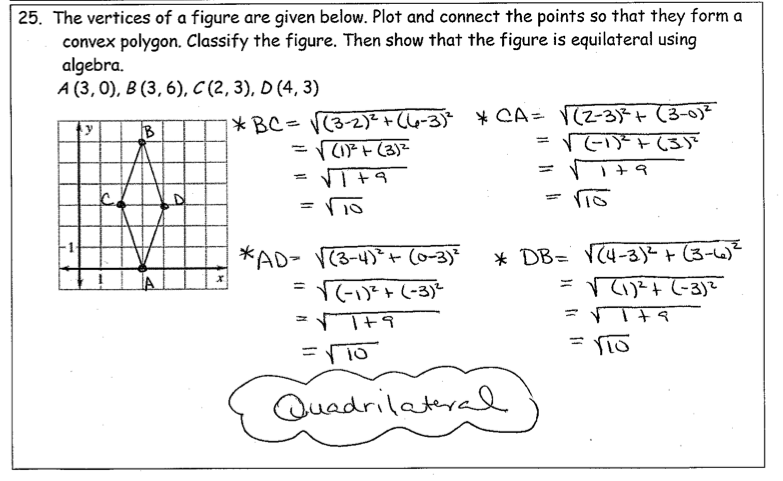
- Geometry Review Worksheet Chapter 1
- Geometry Review Worksheet Chapter 1
- Geometry Review Worksheet Chapter 1
- Geometry Review Worksheet Chapter 1
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What is the definition of a vertical angle?
Vertical angles are a pair of non-adjacent angles formed when two lines intersect. Vertical angles are congruent, meaning they have the same measure, and they are formed opposite each other at the intersection point.
How are vertical angles formed?
Vertical angles are formed when two lines intersect each other, creating four angles. Vertical angles are the pair of angles located opposite each other when the two lines intersect, and they are congruent, meaning they have the same measures.
Are vertical angles congruent or supplementary?
Vertical angles are always congruent. This means that if two lines intersect, forming four angles, the pairs of angles opposite each other (vertical angles) have the same measure. So, vertical angles are congruent, not supplementary.
How do you identify vertical angles in a given figure?
Vertical angles are pairs of angles that are opposite each other when two lines intersect. In a given figure, you can identify vertical angles by locating angles that share a vertex and are not adjacent to each other. These angles will be equal in measure and form an "X" shape when two lines intersect.
What is the sum of the measures of two supplementary angles?
The sum of the measures of two supplementary angles is always 180 degrees.
Can two angles be both vertical and complementary?
No, two angles cannot be both vertical and complementary at the same time. Vertical angles are formed by the intersection of two lines and are congruent, while complementary angles add up to 90 degrees. Since vertical angles are equal to each other, they cannot also be complementary unless they are both 45 degrees.
If two angles are complementary, what is the difference between their measures?
The difference between the measures of two complementary angles is 90 degrees. When two angles are complementary, they add up to 90 degrees, so the difference in their measures is equal to 90 degrees.
Can two angles be both vertical and congruent?
Yes, two angles can be both vertical and congruent. Vertical angles are formed by two intersecting lines and are always congruent. Therefore, if two angles are vertical, they must also be congruent.
How do vertical angles relate to each other in terms of their position in a figure?
Vertical angles are opposite each other when two lines intersect. They are congruent, meaning they have the same measure, and their position in the figure is such that they are located across from each other and do not share a side.
How can you use vertical angles to identify other angle relationships in a figure?
Vertical angles are pairs of angles that are opposite each other when two lines intersect. By identifying vertical angles in a figure, you can determine other angle relationships as well. For example, if you know that two angles are vertical angles, you can conclude that they are congruent. Additionally, vertical angles can be used to identify corresponding angles, alternate interior angles, and alternate exterior angles in a figure, helping you understand the relationships between angles in the geometric configuration.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.




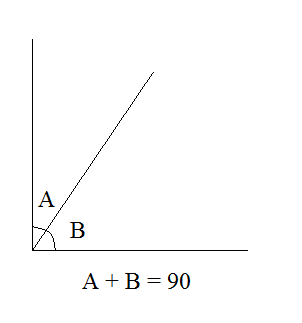














Comments