Unit Circle Worksheet with Answers

The Unit Circle Worksheet with Answers is a valuable resource for students studying trigonometry or preparing for math exams. This comprehensive worksheet provides a clear and concise overview of the unit circle, making it perfect for high school or college-level students seeking to master the concept.

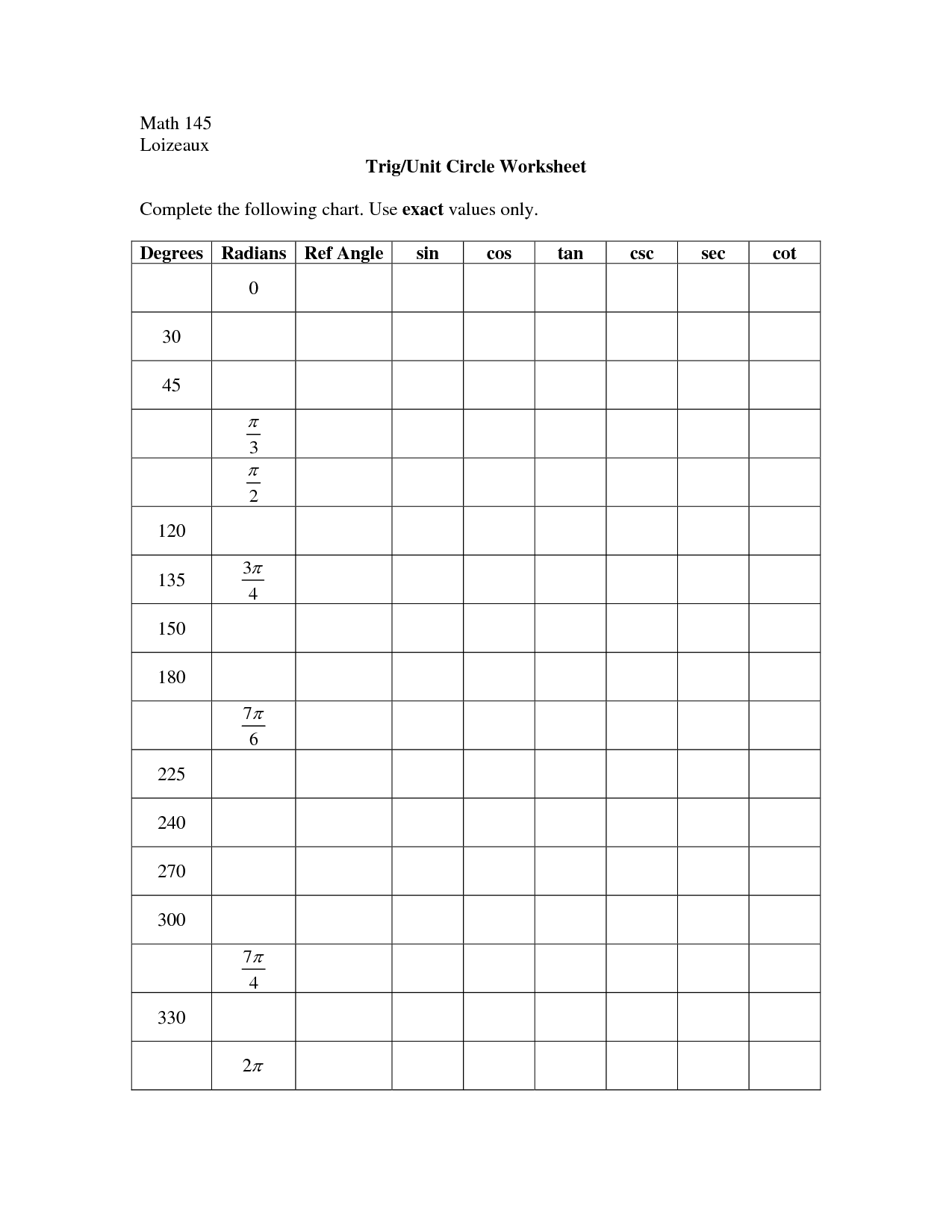
  Trig Unit Circle Worksheet

---

  Unit Circle Worksheet Answers

---

  Unit Circle Worksheet

---

  Calculus Unit Circle

---

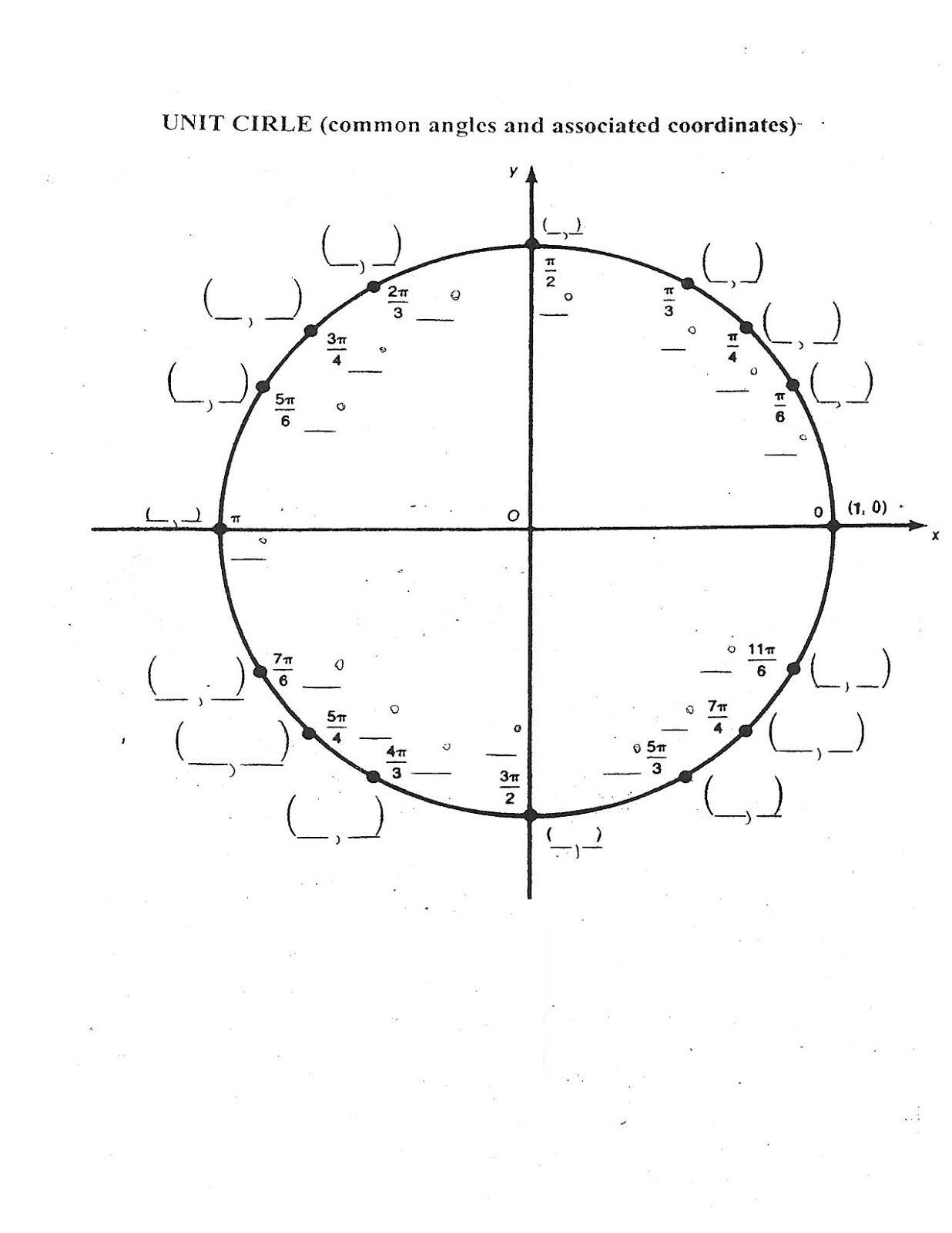
  Blank Unit Circle

---

  Measuring Angles Worksheet Answer

---

  Trig Unit Circle Worksheet

---

  Blank Unit Circle Worksheet

---

  Unit Circle Worksheet

---

  Tangent Unit Circle

---

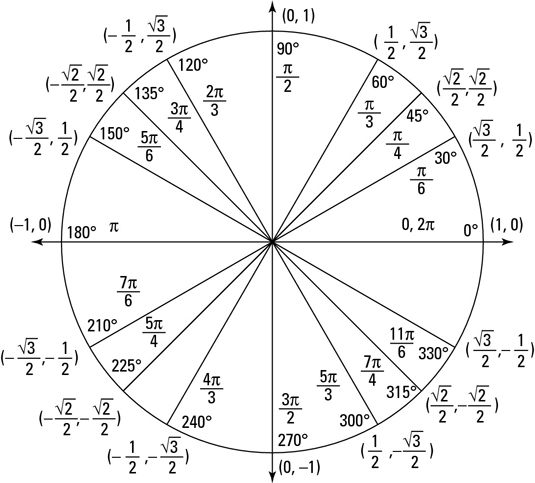
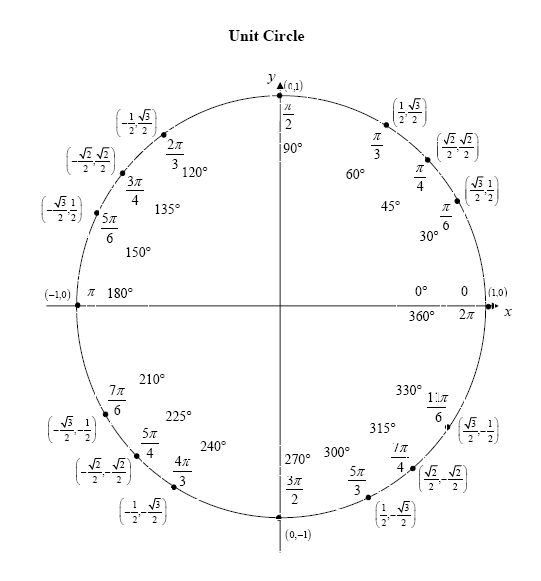
  Unit Circle

---

  Trigonometry Unit Circle Worksheet

---

  Unit Circle Worksheet

---

  Trigonometry Worksheets with Answer Key

---

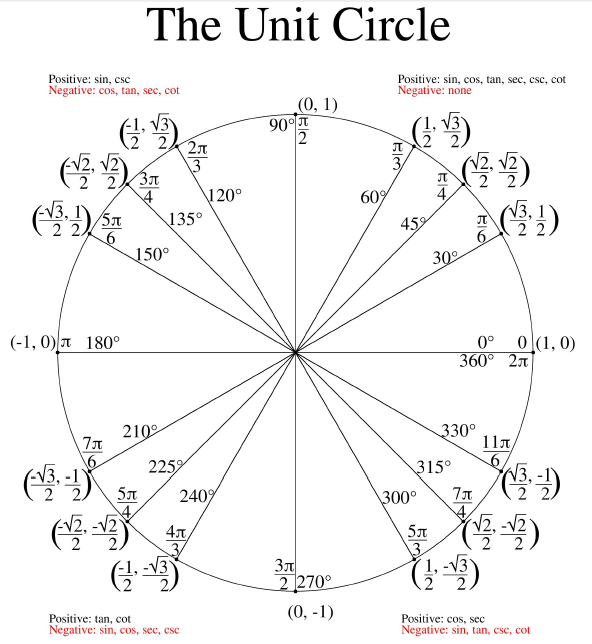
What is the unit circle?

The unit circle is a circle centered at the origin of a coordinate plane with a radius of 1 unit. It is used in mathematics to define trigonometric functions such as sine and cosine, where the point (x, y) on the unit circle corresponds to the values of these functions for a given angle. The unit circle is a fundamental concept in trigonometry and is used to understand relationships between angles and the lengths of sides in right triangles.

What are the coordinates of a point on the unit circle?

A point on the unit circle has coordinates (x, y) where x = cos(theta) and y = sin(theta), for any angle theta.

How is the unit circle used to find trigonometric values?

The unit circle is used to find trigonometric values by associating points on the circle with angles in standard position. The x-coordinate of the point gives the cosine value of the angle, and the y-coordinate gives the sine value. By using the Pythagorean theorem, one can also find the tangent, secant, cosecant, and cotangent values. This method allows for easily determining trigonometric values for angles without having to calculate them individually each time.

What is the definition of sine and cosine on the unit circle?

On the unit circle, the sine of an angle measures the y-coordinate of the point where the terminal side of the angle intersects the unit circle. Likewise, the cosine of an angle measures the x-coordinate of that same point on the unit circle. In simpler terms, the sine is the vertical component, and the cosine is the horizontal component of the point on the unit circle corresponding to the angle.

How are the values of secant and cosecant derived from the unit circle?

The values of secant and cosecant are derived by using the coordinates of a point on the unit circle. Secant is equal to the reciprocal of the x-coordinate of a point on the unit circle, while cosecant is equal to the reciprocal of the y-coordinate. By considering the ratios of side lengths in a right triangle formed by dropping a perpendicular line from the point on the unit circle to the x-axis or y-axis, the values of secant and cosecant can be calculated using the definitions of these trigonometric functions in terms of sine and cosine.

What is the relationship between the unit circle and radians?

The relationship between the unit circle and radians is that the circumference of a unit circle is 2?, which is also equal to 360 degrees. Radians measure angles in terms of the radius of the circle, where 1 radian is equal to the angle subtended at the center of the circle by an arc whose length is equal to the radius of the circle. This relationship is important in trigonometry and calculus, as it allows for a more elegant way of measuring and calculating angles and distances on the circle.

How are tangents and cotangents calculated using the unit circle?

Tangents and cotangents can be calculated using the unit circle by finding the ratios of the coordinates of points on the unit circle. For tangents, it is the y-coordinate divided by the x-coordinate of the point where the terminal arm intersects the unit circle, and for cotangents, it is the reciprocal of the tangent value. This method allows for finding the values of these trigonometric functions without needing to use a calculator or memorizing trigonometric tables.

What are the reference angles in the unit circle?

The reference angles in the unit circle are the angles formed by the terminal side of an angle with the x-axis. These angles are always acute angles that measure between 0 and 90 degrees (or 0 and pi/2 radians), regardless of the quadrant in which the original angle lies. The reference angles provide a way to simplify trigonometric calculations and can be used to find the exact values of trigonometric functions for angles in any quadrant.

What is the significance of the special angles (?/6, ?/4, ?/3, ?/2) in the unit circle?

Special angles (?/6, ?/4, ?/3, ?/2) in the unit circle have significance in trigonometry because they correspond to the trigonometric functions of these angles, making calculations and understanding of trigonometric relationships easier. These angles have predetermined values for sine, cosine, and tangent, which are fractions of common integers, aiding in the simplification of trigonometric expressions and solutions to trigonometric problems. They also form the basis for understanding the behavior of trigonometric functions and their graphs, making them fundamental in trigonometry studies.

How does the unit circle help in solving trigonometric equations and identities?

The unit circle is a powerful tool in solving trigonometric equations and identities because it provides a visual representation of the relationships between trigonometric functions and angles. By placing the unit circle at the center and manipuating angles, one can easily see the values of sine, cosine, and tangent for different angles. This visualization helps in understanding trigonometric identities and simplifying trigonometric equations by leveraging the geometric properties of the unit circle.